|
Michael J. O’Shea
Climbing on Rock
|
|
‘Climbing, slipping and Newton’s second law’, M. J. O’Shea, Phys. Educ. 44 No 6 (November 2009) 644-651. It is possible to model the forces on a climbs hands and feet via Newton’s laws and the use of simple ideas related to static friction. If the climber is inexperienced they tend to lean forward into the rock giving the climber a false sense of security. The climber quickly learns that this can cause their feet to slip out from under them. More experienced climbers will tell the beginner not to lean into the rock but to keep their weight over their feet. The physics behind this is elucidates in this paper.
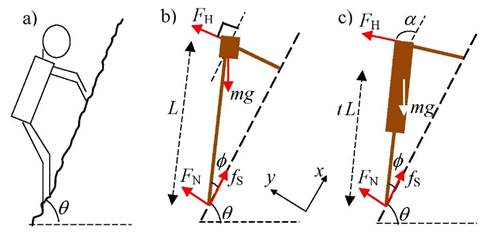
To model the climber on a slope we first consider a point mass model (middle picture) with the arms and legs represented by massless struts. We then generalize to an extended mass model as shown on the far right. We assume the hands are able to get good handholds while the feet are held in place by friction. Clearly this is not always the case but such cases often occur. It is possible in this model to calculate the actual
friction force on the feet of the climber to keep the climber in place, Fs,
and compare this with the maximum possible value of this friction force Fs,max
= mFN (FN is the
normal force on the climber’s feet). This allows us to determine if the
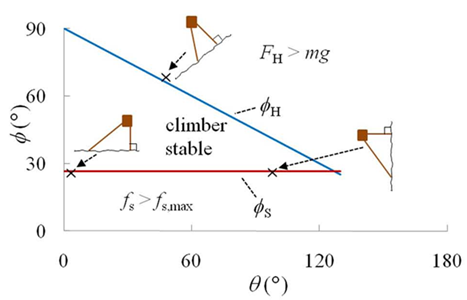
climber is in a stable position. The figure shows the region of stability of
th A problem based on a simple special case can be found here. A problem involving a climber under a roof can be found here. Derivations of the equations of this work can be found here. A spreadsheet that allows you to do calculations for various situations is here.
|