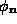 and an out-of-plane angle
and an out-of-plane angle 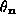 ,
(or spin component), where
,
(or spin component), where 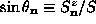 , i.e.,
, i.e.,
We begin by describing how the numerical diagonalization problem for
the normal modes of spinwave motion about a static vortex was set up.
For classical states we can parameterize the spins in terms of an in-plane
angle 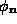 and an out-of-plane angle
and an out-of-plane angle 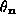 ,
(or spin component), where
,
(or spin component), where 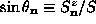 , i.e.,
, i.e.,
For in-plane vortices, the low energy static states of this model will have
all 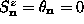 , and then the equation to determine
the in-plane angles becomes
, and then the equation to determine
the in-plane angles becomes
Only when the vortex center 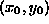 is at a point of high symmetry,
such as the center of a unit cell of the lattice, or directly on a lattice site
(with the spin at that lattice site set perpendicular to the easy-plane) is a
simple analytic solution of Eq. (2.3) known, namely
is at a point of high symmetry,
such as the center of a unit cell of the lattice, or directly on a lattice site
(with the spin at that lattice site set perpendicular to the easy-plane) is a
simple analytic solution of Eq. (2.3) known, namely
where the vorticity q is an integer. For out-of-plane vortices, the in-plane
angles are given by Eq. (2.4), while there are nonzero 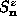 components. In general, for a given value of anisotropy
components. In general, for a given value of anisotropy 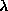 , we have
used a numerical relaxation procedure to determine the static vortex structure,
for either in-plane or out-of-plane vortices. We start with an in-plane
vortex, but perturb the spins in the unit cell containing the vortex core by
giving only those sites small positive
, we have
used a numerical relaxation procedure to determine the static vortex structure,
for either in-plane or out-of-plane vortices. We start with an in-plane
vortex, but perturb the spins in the unit cell containing the vortex core by
giving only those sites small positive 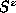 components. Then every spin in
the lattice is re-directed to point along the direction of the effective field
components. Then every spin in
the lattice is re-directed to point along the direction of the effective field
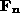 due to its neighbors, as determined from the Hamiltonian
above:
due to its neighbors, as determined from the Hamiltonian
above:
The set 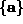 includes only the displacements to the neighbors of site
includes only the displacements to the neighbors of site
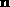 . Sites on the boundary of the finite system will tend to have weaker
effective fields because of their smaller number of nearest neighbors in this
sum. Upon iteration, this procedure relaxes the spins quickly into a static
energy minimum vortex (in-plane or out-of-plane vortex) that is stable for the
given value of anisotropy
. Sites on the boundary of the finite system will tend to have weaker
effective fields because of their smaller number of nearest neighbors in this
sum. Upon iteration, this procedure relaxes the spins quickly into a static
energy minimum vortex (in-plane or out-of-plane vortex) that is stable for the
given value of anisotropy 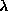 . This is because the spin equations of
motion can be written in the form,
. This is because the spin equations of
motion can be written in the form, 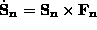 ; the time derivatives vanish when the spins are aligned with
the effective fields of their neighbors. The relaxed vortex configuration,
; the time derivatives vanish when the spins are aligned with
the effective fields of their neighbors. The relaxed vortex configuration,
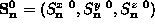 can
then be used to obtain the in-plane and out-of-plane angles of the static
vortex, (
can
then be used to obtain the in-plane and out-of-plane angles of the static
vortex, (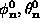 ), using the definition in
Eq. (2.1). Some typical profiles of
), using the definition in
Eq. (2.1). Some typical profiles of 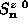 so obtained for
various values of
so obtained for
various values of 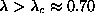 for a circular system on a
square lattice are shown in Fig. 1.
for a circular system on a
square lattice are shown in Fig. 1.