 -axis)
are along the spin directions for the relaxed vortex, while the new
-axis)
are along the spin directions for the relaxed vortex, while the new
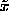 -axis lies in the original xy-plane [See Fig. (2)]:
-axis lies in the original xy-plane [See Fig. (2)]:
Usually, to determine the spinwave spectrum for some system, the
small amplitude spin deviations are assumed to be relative to the local
classical ground state directions. In the case here, the spin deviations are
taken to be relative to a state with one vortex, which is not the ground state,
but is a local energy minimum. Thus we rotate locally into new coordinates at
each site, where the new axes for quantization of each site ( -axis)
are along the spin directions for the relaxed vortex, while the new
-axis)
are along the spin directions for the relaxed vortex, while the new
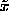 -axis lies in the original xy-plane [See Fig. (2)]:
-axis lies in the original xy-plane [See Fig. (2)]:
Figure 2:
Diagram showing the relation between the original xyz-coordinate
system, and the local coordinates, 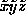 ,
where the
,
where the  -axis lies along the direction of the spin at a particular
site in the unperturbed vortex, and the
-axis lies along the direction of the spin at a particular
site in the unperturbed vortex, and the 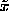 -axis lies in the xy-plane.
-axis lies in the xy-plane.
To simplify the notation that follows, we write
With this transformation, the Hamiltonian in the tilde coordinate system is
The sums are over each bond in the lattice once. Sites on the edge of a finite system will contribute less, due to the smaller number of neighbors for those sites.