


Next: PERTURBATION ABOUT A
Up: NORMAL MODES OF VORTICES
Previous: NORMAL MODES OF VORTICES
In classical models for quasi-two-dimensional magnetic materials[1],
it has been found that vortex nonlinear excitations play an active role in
phase transitions, [2],[3] and are expected to be important
in the spin dynamics. [4],[5],[6] The vortices are
topologically stable excitations, carry effective charges, are created in
particle-antiparticle pairs, and are expected to make contributions to
correlation functions, especially, to central peak intensity in the dynamic
structure function [5] 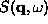 . In particular, in
models of three-component classical spins with easy-plane (XY) anisotropy,
there are two types of vortices possible, [7],[8] known as
``in-plane'' and ``out-of-plane'' vortices, depending on whether the static
vortex has zero or nonzero out-of-easy-plane spin components, respectively.
For ferro- and antiferro-magnets, the static structure of the in-plane vortex
is known exactly, while the static structure of the out-of-plane vortex is only
known approximately (or numerically). Approximate results are also known for
the modification of these spin structures for slowly moving
vortices. [8],[9] Furthermore, the dynamics of pairs of
vortices has received some study; for pairs of out-of-plane vortices, there are
interesting orbital and translational relative motions with faster
cyclotron-like oscillations superimposed. [9],[10],[11]
. In particular, in
models of three-component classical spins with easy-plane (XY) anisotropy,
there are two types of vortices possible, [7],[8] known as
``in-plane'' and ``out-of-plane'' vortices, depending on whether the static
vortex has zero or nonzero out-of-easy-plane spin components, respectively.
For ferro- and antiferro-magnets, the static structure of the in-plane vortex
is known exactly, while the static structure of the out-of-plane vortex is only
known approximately (or numerically). Approximate results are also known for
the modification of these spin structures for slowly moving
vortices. [8],[9] Furthermore, the dynamics of pairs of
vortices has received some study; for pairs of out-of-plane vortices, there are
interesting orbital and translational relative motions with faster
cyclotron-like oscillations superimposed. [9],[10],[11]
Some attempts have been made to describe these motions as found from numerical
simulations by effective equations of motion for the vortex
centers, [4],[12],[13] including effective masses and
charges [11],[14],[15] that determine the dynamics
(collective coordinates. [16]) However, these approaches have
assumed that a vortex has no internal dynamics, that a moving vortex consists
of a uniformly translating spin profile of fixed shape, with no internal
oscillations or other intrinsic time dependence. However, it is expected that
the vortex spin profile can have some kind of internal oscillation, perhaps
even when it is stationary (i.e., not translating), in analogy with the
internal modes of nonlinear excitations in one dimension. [17]
Little is known about such dynamic modes of individual vortices. A description
of their properties could be valuable in application to the collective
coordinate theory [18] and in calculations of dynamic response
functions. These modes can be determined, however, by evaluating through
numerical diagonalization the small amplitude normal modes of oscillation of
the spin field about a single vortex. The resulting spinwave spectrum may
contain particular modes that are strongly associated with the presence of the
vortex itself, and otherwise absent if the vortex is absent. It is likely that
these modes would be localized on the vortex. In addition, the spectrum will
contain other modes that are extended over the entire system, and possibly only
modified slightly by the presence of the vortex. Those modes, however, will
contain information about the interaction of the spinwaves with the vortex.
For these reasons, we investigate numerically the spinwave modes of a system
containing an individual vortex, and analyze one particular spinwave mode that
is responsible for an intrinsic instability [8],[19] of the
in-plane vortex towards developing large out-of-plane spin components and
becoming an out-of-plane vortex as the easy-plane anisotropy is reduced.
Specifially, we consider a set of classical spin variables on a two-dimensional
(2D) lattice, interacting with easy-plane anisotropic near neighbor exchange.
The easy-plane anisotropy will be described by the parameter 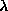 (
(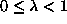 ) in the following Hamiltonian:
) in the following Hamiltonian:
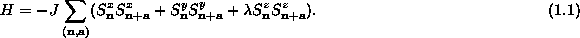
The sum is over nearest neighbor pairs of spins
S on a 2D lattice with sites 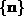 , and the set of displacements to the
nearest neighbors is
, and the set of displacements to the
nearest neighbors is 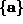 .
.
Much of the theory for magnetic vortices in this model has been developed in
continuum limits. In the present context, Costa et al. [20]
and Pereira et al. [21] have considered the spinwave modes
about single vortices and vortex-antivortex pairs [22] in the XY
model (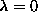 ), using a continuum limit description of the lattice.
However, a continuum description of a magnetic vortex on a lattice presents
difficulties, because the spin field varies rapidly from one lattice site to
the next in the core region of the vortex, violating the usual continuum
assumptions. Also, the short distance cutoff (for example, in energy
integrals) in the continuum theory is not well-prescribed, whereas these
difficulties do not appear if one solves for the spinwave modes in the original
lattice model. For these reasons, we consider vortices in this model on a
lattice, where the discrete lattice effects, that are most influential in the
core of the vortex, can be correctly accounted for.
), using a continuum limit description of the lattice.
However, a continuum description of a magnetic vortex on a lattice presents
difficulties, because the spin field varies rapidly from one lattice site to
the next in the core region of the vortex, violating the usual continuum
assumptions. Also, the short distance cutoff (for example, in energy
integrals) in the continuum theory is not well-prescribed, whereas these
difficulties do not appear if one solves for the spinwave modes in the original
lattice model. For these reasons, we consider vortices in this model on a
lattice, where the discrete lattice effects, that are most influential in the
core of the vortex, can be correctly accounted for.
It is well-established that for this model with a specified strength of
easy-plane anisotropy, only one of the vortex types is numerically stable when
placed on a lattice. [8],[19] Numerical simulations have led to
the conclusion that static in-plane vortices are stable only when 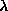 is
less than a critical value
is
less than a critical value 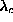 . On the other hand, static
out-of-plane vortices are stable only when
. On the other hand, static
out-of-plane vortices are stable only when 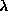 is greater than
is greater than
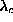 . To say that one type is unstable means that it will evolve into
the other type. The critical value
. To say that one type is unstable means that it will evolve into
the other type. The critical value 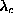 was found to have a
substantial lattice-dependence;
was found to have a
substantial lattice-dependence; 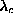 is approximately 0.62, 0.70,
0.84, for triangular, square, and hexagonal lattices, respectively (for
ferromagnets). This strong lattice dependence is due partly to the
discreteness effects near the vortex core, for which the usual continuum limit
theories are likely to be inadequate.
is approximately 0.62, 0.70,
0.84, for triangular, square, and hexagonal lattices, respectively (for
ferromagnets). This strong lattice dependence is due partly to the
discreteness effects near the vortex core, for which the usual continuum limit
theories are likely to be inadequate.
This instability or crossover has been found to be driven by a particular
dynamic mode of the in-plane vortex, [23] whose frequency goes to
zero as 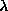 approaches
approaches 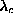 . Preliminary numerical
diagonalizations were made for the spinwave modes of a
. Preliminary numerical
diagonalizations were made for the spinwave modes of a 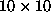 square
lattice system containing one vortex, with a free boundary
condition. [9],[24] A mode that became soft was found to have
its amplitude concentrated near the center of the vortex, suggesting that it is
a localized mode associated with the presence of the vortex, as opposed to an
extended continuum spinwave mode of the entire system. More recently, an
Ansatz was made for the structure of a vortex on a lattice, [23] in
order to explain the lattice dependence of
square
lattice system containing one vortex, with a free boundary
condition. [9],[24] A mode that became soft was found to have
its amplitude concentrated near the center of the vortex, suggesting that it is
a localized mode associated with the presence of the vortex, as opposed to an
extended continuum spinwave mode of the entire system. More recently, an
Ansatz was made for the structure of a vortex on a lattice, [23] in
order to explain the lattice dependence of 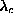 . In this Ansatz, it
was assumed that only a small set of spins near the core of the vortex could
have nonzero out-of-plane spin components, while all other spins farther out
from the core were held fixed in the easy plane. The out-of-plane spin
components were assumed to depend only on the radial distance from the vortex
center. The analysis was used to determine very accurately the values of
. In this Ansatz, it
was assumed that only a small set of spins near the core of the vortex could
have nonzero out-of-plane spin components, while all other spins farther out
from the core were held fixed in the easy plane. The out-of-plane spin
components were assumed to depend only on the radial distance from the vortex
center. The analysis was used to determine very accurately the values of
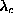 for the different lattices mentioned above. More importantly, it
also was used to make estimates of the frequency of the dynamic mode
responsible for the in-plane to out-of-plane vortex crossover. However, it is
clear that a more complete analysis of the spinwave modes about a static vortex
is needed, especially including an understanding of how that eigenfrequency
depends on the system size.
for the different lattices mentioned above. More importantly, it
also was used to make estimates of the frequency of the dynamic mode
responsible for the in-plane to out-of-plane vortex crossover. However, it is
clear that a more complete analysis of the spinwave modes about a static vortex
is needed, especially including an understanding of how that eigenfrequency
depends on the system size.
Therefore, we have made a set of numerical diagonalizations for finite systems,
to obtain the normal modes (i.e., spinwaves) in the presence of a single
in-plane vortex for  , and in the presence of a single
out-of-plane vortex for
, and in the presence of a single
out-of-plane vortex for 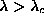 . The calculations described here
are semiclassical; the spin equations of motion have been linearized about a
numerically-determined static vortex solution, using local Cartesian spin
components with different local spin axes at each site. The notation for the
calculation is described in the following section. Approximately circular
systems on triangular, square, and hexagonal lattices were used. A set of
calculations was performed for each lattice, with a range of system sizes. For
each system used, the dependence of the eigenspectrum on the anisotropy
. The calculations described here
are semiclassical; the spin equations of motion have been linearized about a
numerically-determined static vortex solution, using local Cartesian spin
components with different local spin axes at each site. The notation for the
calculation is described in the following section. Approximately circular
systems on triangular, square, and hexagonal lattices were used. A set of
calculations was performed for each lattice, with a range of system sizes. For
each system used, the dependence of the eigenspectrum on the anisotropy
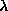 was determined. This includes measuring the rms ``sizes'' of the
wavefunctions associated with the modes, and comparing to the size of the
finite system that was used, to decide which modes are localized and which are
extended. The mode whose frequency approaches zero as
was determined. This includes measuring the rms ``sizes'' of the
wavefunctions associated with the modes, and comparing to the size of the
finite system that was used, to decide which modes are localized and which are
extended. The mode whose frequency approaches zero as 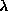 approaches
approaches
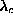 has occupied much of our attention. We give substantial analysis
of its dependence on
has occupied much of our attention. We give substantial analysis
of its dependence on 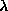 , the type of lattice, and the system size.
, the type of lattice, and the system size.



Next: PERTURBATION ABOUT A
Up: NORMAL MODES OF VORTICES
Previous: NORMAL MODES OF VORTICES
Gary M Wysin
Mon Sep 11 12:02:10 CDT 1995
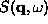 . In particular, in
models of three-component classical spins with easy-plane (XY) anisotropy,
there are two types of vortices possible, [7],[8] known as
``in-plane'' and ``out-of-plane'' vortices, depending on whether the static
vortex has zero or nonzero out-of-easy-plane spin components, respectively.
For ferro- and antiferro-magnets, the static structure of the in-plane vortex
is known exactly, while the static structure of the out-of-plane vortex is only
known approximately (or numerically). Approximate results are also known for
the modification of these spin structures for slowly moving
vortices. [8],[9] Furthermore, the dynamics of pairs of
vortices has received some study; for pairs of out-of-plane vortices, there are
interesting orbital and translational relative motions with faster
cyclotron-like oscillations superimposed. [9],[10],[11]
. In particular, in
models of three-component classical spins with easy-plane (XY) anisotropy,
there are two types of vortices possible, [7],[8] known as
``in-plane'' and ``out-of-plane'' vortices, depending on whether the static
vortex has zero or nonzero out-of-easy-plane spin components, respectively.
For ferro- and antiferro-magnets, the static structure of the in-plane vortex
is known exactly, while the static structure of the out-of-plane vortex is only
known approximately (or numerically). Approximate results are also known for
the modification of these spin structures for slowly moving
vortices. [8],[9] Furthermore, the dynamics of pairs of
vortices has received some study; for pairs of out-of-plane vortices, there are
interesting orbital and translational relative motions with faster
cyclotron-like oscillations superimposed. [9],[10],[11]
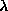 (
(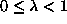 ) in the following Hamiltonian:
) in the following Hamiltonian:
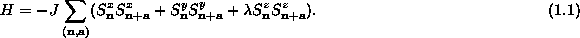
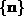 , and the set of displacements to the
nearest neighbors is
, and the set of displacements to the
nearest neighbors is 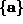 .
.
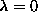 ), using a continuum limit description of the lattice.
However, a continuum description of a magnetic vortex on a lattice presents
difficulties, because the spin field varies rapidly from one lattice site to
the next in the core region of the vortex, violating the usual continuum
assumptions. Also, the short distance cutoff (for example, in energy
integrals) in the continuum theory is not well-prescribed, whereas these
difficulties do not appear if one solves for the spinwave modes in the original
lattice model. For these reasons, we consider vortices in this model on a
lattice, where the discrete lattice effects, that are most influential in the
core of the vortex, can be correctly accounted for.
), using a continuum limit description of the lattice.
However, a continuum description of a magnetic vortex on a lattice presents
difficulties, because the spin field varies rapidly from one lattice site to
the next in the core region of the vortex, violating the usual continuum
assumptions. Also, the short distance cutoff (for example, in energy
integrals) in the continuum theory is not well-prescribed, whereas these
difficulties do not appear if one solves for the spinwave modes in the original
lattice model. For these reasons, we consider vortices in this model on a
lattice, where the discrete lattice effects, that are most influential in the
core of the vortex, can be correctly accounted for.
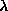 is
less than a critical value
is
less than a critical value 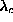 . On the other hand, static
out-of-plane vortices are stable only when
. On the other hand, static
out-of-plane vortices are stable only when 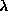 is greater than
is greater than
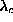 . To say that one type is unstable means that it will evolve into
the other type. The critical value
. To say that one type is unstable means that it will evolve into
the other type. The critical value 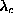 was found to have a
substantial lattice-dependence;
was found to have a
substantial lattice-dependence; 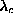 is approximately 0.62, 0.70,
0.84, for triangular, square, and hexagonal lattices, respectively (for
ferromagnets). This strong lattice dependence is due partly to the
discreteness effects near the vortex core, for which the usual continuum limit
theories are likely to be inadequate.
is approximately 0.62, 0.70,
0.84, for triangular, square, and hexagonal lattices, respectively (for
ferromagnets). This strong lattice dependence is due partly to the
discreteness effects near the vortex core, for which the usual continuum limit
theories are likely to be inadequate.
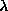 approaches
approaches 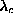 . Preliminary numerical
diagonalizations were made for the spinwave modes of a
. Preliminary numerical
diagonalizations were made for the spinwave modes of a 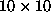 square
lattice system containing one vortex, with a free boundary
condition. [
square
lattice system containing one vortex, with a free boundary
condition. [ . In this Ansatz, it
was assumed that only a small set of spins near the core of the vortex could
have nonzero out-of-plane spin components, while all other spins farther out
from the core were held fixed in the easy plane. The out-of-plane spin
components were assumed to depend only on the radial distance from the vortex
center. The analysis was used to determine very accurately the values of
. In this Ansatz, it
was assumed that only a small set of spins near the core of the vortex could
have nonzero out-of-plane spin components, while all other spins farther out
from the core were held fixed in the easy plane. The out-of-plane spin
components were assumed to depend only on the radial distance from the vortex
center. The analysis was used to determine very accurately the values of
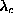 for the different lattices mentioned above. More importantly, it
also was used to make estimates of the frequency of the dynamic mode
responsible for the in-plane to out-of-plane vortex crossover. However, it is
clear that a more complete analysis of the spinwave modes about a static vortex
is needed, especially including an understanding of how that eigenfrequency
depends on the system size.
for the different lattices mentioned above. More importantly, it
also was used to make estimates of the frequency of the dynamic mode
responsible for the in-plane to out-of-plane vortex crossover. However, it is
clear that a more complete analysis of the spinwave modes about a static vortex
is needed, especially including an understanding of how that eigenfrequency
depends on the system size.
 , and in the presence of a single
out-of-plane vortex for
, and in the presence of a single
out-of-plane vortex for 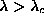 . The calculations described here
are semiclassical; the spin equations of motion have been linearized about a
numerically-determined static vortex solution, using local Cartesian spin
components with different local spin axes at each site. The notation for the
calculation is described in the following section. Approximately circular
systems on triangular, square, and hexagonal lattices were used. A set of
calculations was performed for each lattice, with a range of system sizes. For
each system used, the dependence of the eigenspectrum on the anisotropy
. The calculations described here
are semiclassical; the spin equations of motion have been linearized about a
numerically-determined static vortex solution, using local Cartesian spin
components with different local spin axes at each site. The notation for the
calculation is described in the following section. Approximately circular
systems on triangular, square, and hexagonal lattices were used. A set of
calculations was performed for each lattice, with a range of system sizes. For
each system used, the dependence of the eigenspectrum on the anisotropy
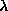 was determined. This includes measuring the rms ``sizes'' of the
wavefunctions associated with the modes, and comparing to the size of the
finite system that was used, to decide which modes are localized and which are
extended. The mode whose frequency approaches zero as
was determined. This includes measuring the rms ``sizes'' of the
wavefunctions associated with the modes, and comparing to the size of the
finite system that was used, to decide which modes are localized and which are
extended. The mode whose frequency approaches zero as 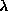 approaches
approaches
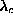 has occupied much of our attention. We give substantial analysis
of its dependence on
has occupied much of our attention. We give substantial analysis
of its dependence on 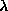 , the type of lattice, and the system size.
, the type of lattice, and the system size.