


Next: The Broken Symmetry
Up: Discussion and Conclusions
Previous: Effect of Vortex
To obtain one more way to understand the degeneracies, we can plot the complete
wavefunctions, including the phase information. This can be done by drawing an
arrow in the complex plane for each lattice site, where the length of the arrow
is proportional to 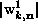 , and the direction of the arrow
is determined by the phase of
, and the direction of the arrow
is determined by the phase of 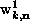 . Similar arrows can be
drawn for the other component of the wavefunction,
. Similar arrows can be
drawn for the other component of the wavefunction, 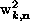 .
For in-plane vortices,
.
For in-plane vortices, 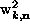 represents the in-plane spin
fluctuations, while
represents the in-plane spin
fluctuations, while 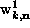 represents the out-of-plane spin
fluctuations. For out-of-plane vortices,
represents the out-of-plane spin
fluctuations. For out-of-plane vortices, 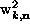 represents only a part of the in-plane spin fluctuations, while
represents only a part of the in-plane spin fluctuations, while 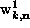 represents a combination of out-of-plane and in-plane spin
fluctuations, depending on the static out-of-plane spin structure. This
interesting representation of the two modes (b1) and (b2) is shown in Fig.
13, for
represents a combination of out-of-plane and in-plane spin
fluctuations, depending on the static out-of-plane spin structure. This
interesting representation of the two modes (b1) and (b2) is shown in Fig.
13, for 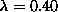 , well below
, well below 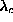 . Here we clearly
see the distinction between these degenenerate modes, which is made in terms of
the phase of the spinwave and the way it changes around the center
position of the vortex. Mode (b2) has the phase of both components
. Here we clearly
see the distinction between these degenenerate modes, which is made in terms of
the phase of the spinwave and the way it changes around the center
position of the vortex. Mode (b2) has the phase of both components
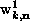 and
and 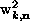 changing in the positive
sense around the vortex center, while mode (b1) has the phase of both
components changing in the negative sense around the vortex center. Of
course, this representation is not unique; we could make linear combinations of
these two modes and produce equivalent wavefunctions that do not have this
``vortexlike'' and ``antivortex-like'' appearance, but which would produce
squared wavefunctions more like those already shown for
changing in the positive
sense around the vortex center, while mode (b1) has the phase of both
components changing in the negative sense around the vortex center. Of
course, this representation is not unique; we could make linear combinations of
these two modes and produce equivalent wavefunctions that do not have this
``vortexlike'' and ``antivortex-like'' appearance, but which would produce
squared wavefunctions more like those already shown for 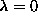 in Fig.
7b1 and Fig. 7b2.
in Fig.
7b1 and Fig. 7b2.

Figure 13:
Wavefunctions for the lowest degenerate modes (b1) and (b2) in the 180
site square lattice system
with a vortex at the center, at 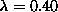 , well below
, well below 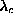 .
The line-head arrows are the complex amplitudes
.
The line-head arrows are the complex amplitudes 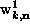 , and the
hollow-head arrows are the complex amplitudes
, and the
hollow-head arrows are the complex amplitudes 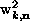 . The relative
sizes and phases of these amplitudes are preserved in these diagrams.
. The relative
sizes and phases of these amplitudes are preserved in these diagrams.
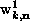 relates to the out-of-plane spin fluctuations,
and
relates to the out-of-plane spin fluctuations,
and 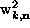 relates to the in-plane spin fluctuations.
The frequency of these modes is
relates to the in-plane spin fluctuations.
The frequency of these modes is 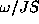 =0.6776 .
=0.6776 .

Figure 14:
Wavefunctions for the modes (b1) and (b2) in the 180 site system with
a vortex at the center, as in Fig. 13, but for
 , just above
, just above 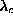 , where they are now nondegenerate.
Mode (b1) has frequency
, where they are now nondegenerate.
Mode (b1) has frequency 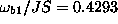 , and mode (b2) has frequency
, and mode (b2) has frequency
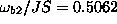 .
.



Next: The Broken Symmetry
Up: Discussion and Conclusions
Previous: Effect of Vortex
Gary M Wysin
Mon Sep 11 12:02:10 CDT 1995
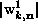 , and the direction of the arrow
is determined by the phase of
, and the direction of the arrow
is determined by the phase of 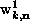 . Similar arrows can be
drawn for the other component of the wavefunction,
. Similar arrows can be
drawn for the other component of the wavefunction, 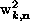 .
For in-plane vortices,
.
For in-plane vortices, 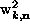 represents the in-plane spin
fluctuations, while
represents the in-plane spin
fluctuations, while 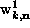 represents the out-of-plane spin
fluctuations. For out-of-plane vortices,
represents the out-of-plane spin
fluctuations. For out-of-plane vortices, 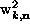 represents only a part of the in-plane spin fluctuations, while
represents only a part of the in-plane spin fluctuations, while 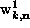 represents a combination of out-of-plane and in-plane spin
fluctuations, depending on the static out-of-plane spin structure. This
interesting representation of the two modes (b1) and (b2) is shown in Fig.
13, for
represents a combination of out-of-plane and in-plane spin
fluctuations, depending on the static out-of-plane spin structure. This
interesting representation of the two modes (b1) and (b2) is shown in Fig.
13, for 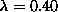 , well below
, well below 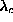 . Here we clearly
see the distinction between these degenenerate modes, which is made in terms of
the phase of the spinwave and the way it changes around the center
position of the vortex. Mode (b2) has the phase of both components
. Here we clearly
see the distinction between these degenenerate modes, which is made in terms of
the phase of the spinwave and the way it changes around the center
position of the vortex. Mode (b2) has the phase of both components
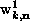 and
and 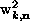 changing in the positive
sense around the vortex center, while mode (b1) has the phase of both
components changing in the negative sense around the vortex center. Of
course, this representation is not unique; we could make linear combinations of
these two modes and produce equivalent wavefunctions that do not have this
``vortexlike'' and ``antivortex-like'' appearance, but which would produce
squared wavefunctions more like those already shown for
changing in the positive
sense around the vortex center, while mode (b1) has the phase of both
components changing in the negative sense around the vortex center. Of
course, this representation is not unique; we could make linear combinations of
these two modes and produce equivalent wavefunctions that do not have this
``vortexlike'' and ``antivortex-like'' appearance, but which would produce
squared wavefunctions more like those already shown for 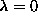 in Fig.
7b1 and Fig. 7b2.
in Fig.
7b1 and Fig. 7b2.

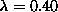 , well below
, well below 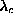 .
The line-head arrows are the complex amplitudes
.
The line-head arrows are the complex amplitudes 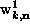 , and the
hollow-head arrows are the complex amplitudes
, and the
hollow-head arrows are the complex amplitudes 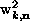 . The relative
sizes and phases of these amplitudes are preserved in these diagrams.
. The relative
sizes and phases of these amplitudes are preserved in these diagrams.
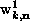 relates to the out-of-plane spin fluctuations,
and
relates to the out-of-plane spin fluctuations,
and 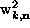 relates to the in-plane spin fluctuations.
The frequency of these modes is
relates to the in-plane spin fluctuations.
The frequency of these modes is 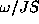 =0.6776 .
=0.6776 . 
 , just above
, just above 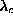 , where they are now nondegenerate.
Mode (b1) has frequency
, where they are now nondegenerate.
Mode (b1) has frequency 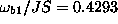 , and mode (b2) has frequency
, and mode (b2) has frequency
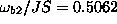 .
.