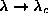The above results show how there is one particular mode that goes soft
for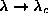 
. To get a better idea of the
physical structure of this mode or any of the modes, it is
necessary to look at the associated wavefunctions.
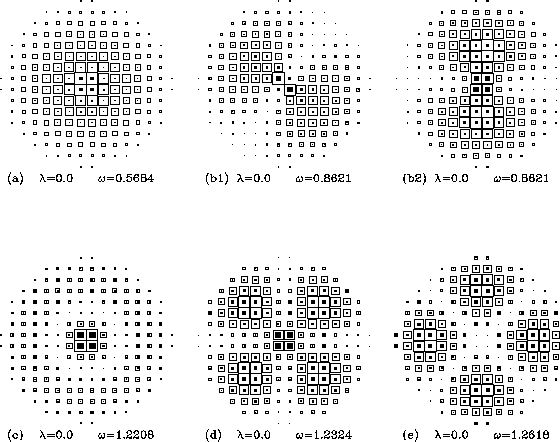
Figure:
Maps of the spin fluctuations in a square lattice system with 180 sites, for
the six lowest frequency modes when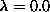 
Out-of-plane fluctuations
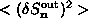(Eq. 3.13b) are proportional to the
areas of the solid squares. In-plane fluctuations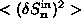 
(Eq. 3.13a) are proportional to the white area within the
larger squares. The total in-plane plus out-of-plane fluctuations are
proportional to the areas of the larger squares. Part (a) shows the soft mode,
while (b1) and (b2) are a degenerate pair, and (c), (d) and (e)
are the next higher frequency modes.
Also, it is important to measure the spread
of the wavefunctions, to understand whether a particular mode is
localized on the vortex or extended throughout the system. For a system
with 180 spins, the wavefunctions of the six lowest energy modes are shown in
Figs. 7, 8, 9 , for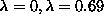 
,
and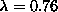 
, corresponding to well below 
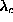, just below
, and slightly above 
.
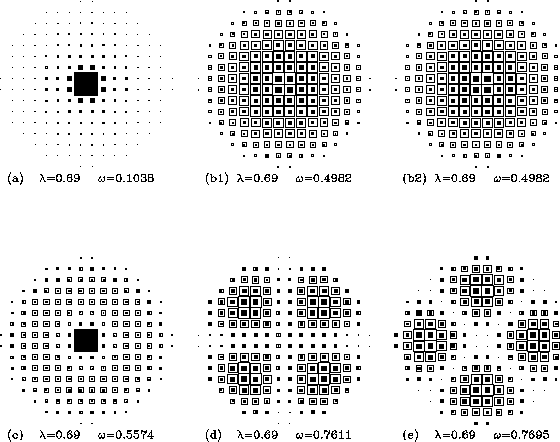
Figure 8:
Maps of the spin fluctuations in the square lattice system
as in Fig. 7, but for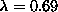 
, just below the transition to
an out-of-plane vortex. In (a), the soft mode's intensity
concentrates itself more near the vortex core, and is strongly out-of-plane,
while the higher modes in (b) through (e) have much smaller changes from
their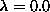 
forms.
In these diagrams, two squares representing the squared wavefunction are
plotted at each lattice site, in order to present both the in-plane and
out-of-plane fluctuations for the selected mode on one diagram. The area of
the inner solid square is proportional to the out-of-plane spin fluctuations
for that site, as in Eq. (3.13b). The area of the larger open square is
proportional to the total in-plane plus out-of-plane spin fluctuations, as in
Eq. (3.13). The difference of the two areas (the white area outside
the solid square, and inside the open square) is proportional to the in-plane
spin fluctuations, as in Eq. (3.13a). For the soft mode (a), there is a
substantial increase in the out-of-plane fluctuations as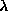 
approaches
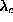, while the relative size of the in-plane fluctuations
diminishes. For the other lowest modes, there are only minor changes in the
fluctuations with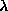 
. The mode labeled (b) is doubly degenerate, while
(b1) and (b2) are its two components that are split above
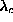[Fig. 9]. Also note that the orientation of the two components
of this mode is rather arbitrary, because there is an arbitrary phase between
the two modes involved. This is the cause for the oblique angle of the line of
nodes in mode (b1) in Figures 7 and 10.
For comparison, Fig. 10 shows the lowest modes on the 180-site system
in the absence of the vortex, at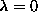 
, starting instead from a
ferromagnetically aligned state. Some modes, including the one that most
resembles the soft mode when the vortex is present, do not appear very
different whether the vortex is present or absent (for this value of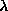 
far from 
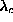). On the other hand, some modes, such as (b) and (d),
clearly have amplitude at the vortex core that is not present when the vortex
is removed.
Figure 9:
Maps of the spin fluctuations in the square lattice system
as in Fig. 7, but for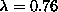 
, above 
.
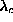The soft mode in (a) is strongly out-of-plane, with intensity concentrated
near the vortex core, while mode (b)'s degeneracy is now split.