


Next: Finite Size and
Up: Discussion and Conclusions
Previous: Complete Wavefunction Phase
This representation has the great advantage that it contains the physical
explanation of how the symmetry is broken; for 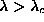 , once
there are static out-of-plane spin components, the two different senses of
change in the spinwave phase are not equivalent. Then mode (b1), with its
phase changing in the negative sense around the vortex center, falls lower than
mode (b2). The two wavefunctions are shown in Fig. 14, for
, once
there are static out-of-plane spin components, the two different senses of
change in the spinwave phase are not equivalent. Then mode (b1), with its
phase changing in the negative sense around the vortex center, falls lower than
mode (b2). The two wavefunctions are shown in Fig. 14, for
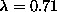 , just above
, just above 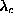 . Once there are nonzero
. Once there are nonzero 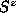 spin
components in the static vortex structure, this lack of equivalence for the
two senses of rotation of the phase is very reasonable. It can also explain
the higher degenerate pairs, because they also have the spinwave phase changing
smoothly as one moves around the vortex center, some with higher winding
numbers---the phase change of the spinwave in these cases changes by
spin
components in the static vortex structure, this lack of equivalence for the
two senses of rotation of the phase is very reasonable. It can also explain
the higher degenerate pairs, because they also have the spinwave phase changing
smoothly as one moves around the vortex center, some with higher winding
numbers---the phase change of the spinwave in these cases changes by 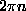 ,
where n is an integer [See Fig. 15]. Furthermore, this
viewpoint shows why all of these degeneracies are split at
,
where n is an integer [See Fig. 15]. Furthermore, this
viewpoint shows why all of these degeneracies are split at 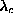 ,
because the plus and minus senses of rotation of the phase are not equivalent,
no matter what the winding number. Conversely, the modes that do not occur as
degenerate pairs do not have a slow change in the phase around the vortex
center. This new effect might be described as a coupling of the vorticity of
the original vortex to the winding number of the phase of its spinwave
excitations. Further details on the forms and characteristics of these
wavefunctions will be published elsewhere.
,
because the plus and minus senses of rotation of the phase are not equivalent,
no matter what the winding number. Conversely, the modes that do not occur as
degenerate pairs do not have a slow change in the phase around the vortex
center. This new effect might be described as a coupling of the vorticity of
the original vortex to the winding number of the phase of its spinwave
excitations. Further details on the forms and characteristics of these
wavefunctions will be published elsewhere.

Figure 15:
Wavefunctions for the third lowest degenerate pair of modes of the
180 site system with a vortex at it center, as in Fig. 13,
at 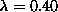 . The frequency of these modes is
. The frequency of these modes is 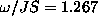 ,
and they have winding numbers -3 and +3.
,
and they have winding numbers -3 and +3.



Next: Finite Size and
Up: Discussion and Conclusions
Previous: Complete Wavefunction Phase
Gary M Wysin
Mon Sep 11 12:02:10 CDT 1995
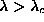 , once
there are static out-of-plane spin components, the two different senses of
change in the spinwave phase are not equivalent. Then mode (b1), with its
phase changing in the negative sense around the vortex center, falls lower than
mode (b2). The two wavefunctions are shown in Fig. 14, for
, once
there are static out-of-plane spin components, the two different senses of
change in the spinwave phase are not equivalent. Then mode (b1), with its
phase changing in the negative sense around the vortex center, falls lower than
mode (b2). The two wavefunctions are shown in Fig. 14, for
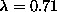 , just above
, just above 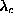 . Once there are nonzero
. Once there are nonzero 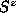 spin
components in the static vortex structure, this lack of equivalence for the
two senses of rotation of the phase is very reasonable. It can also explain
the higher degenerate pairs, because they also have the spinwave phase changing
smoothly as one moves around the vortex center, some with higher winding
numbers---the phase change of the spinwave in these cases changes by
spin
components in the static vortex structure, this lack of equivalence for the
two senses of rotation of the phase is very reasonable. It can also explain
the higher degenerate pairs, because they also have the spinwave phase changing
smoothly as one moves around the vortex center, some with higher winding
numbers---the phase change of the spinwave in these cases changes by 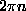 ,
where n is an integer [See Fig. 15]. Furthermore, this
viewpoint shows why all of these degeneracies are split at
,
where n is an integer [See Fig. 15]. Furthermore, this
viewpoint shows why all of these degeneracies are split at 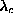 ,
because the plus and minus senses of rotation of the phase are not equivalent,
no matter what the winding number. Conversely, the modes that do not occur as
degenerate pairs do not have a slow change in the phase around the vortex
center. This new effect might be described as a coupling of the vorticity of
the original vortex to the winding number of the phase of its spinwave
excitations. Further details on the forms and characteristics of these
wavefunctions will be published elsewhere.
,
because the plus and minus senses of rotation of the phase are not equivalent,
no matter what the winding number. Conversely, the modes that do not occur as
degenerate pairs do not have a slow change in the phase around the vortex
center. This new effect might be described as a coupling of the vorticity of
the original vortex to the winding number of the phase of its spinwave
excitations. Further details on the forms and characteristics of these
wavefunctions will be published elsewhere.

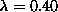 . The frequency of these modes is
. The frequency of these modes is 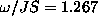 ,
and they have winding numbers -3 and +3.
,
and they have winding numbers -3 and +3.