


Next: Complete Wavefunction Phase
Up: Discussion and Conclusions
Previous: Discussion and Conclusions
We have found that some of the higher modes also have strong changes associated
with the vortex instability; partial evidence is the downward cusps in the
spectrum.[27] Additional evidence appears in the wavefunctions
themselves. For example, mode (c) (third lowest in Fig. 3b) is one
of the modes with a cusp, and for 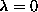 , there is not too much difference
in this mode's structure, regardless of the presence or absence of the vortex
[compare Fig. 7c and Fig. 10c], except that the mode is more
concentrated at the system center when the vortex is present. However, this
mode also concentrates itself additionally onto the vortex core for
, there is not too much difference
in this mode's structure, regardless of the presence or absence of the vortex
[compare Fig. 7c and Fig. 10c], except that the mode is more
concentrated at the system center when the vortex is present. However, this
mode also concentrates itself additionally onto the vortex core for 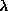 near
near 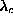 , just as mode (a) does, as seen in Fig. 8c.
Presumably, the other modes higher up in the spectrum that possess downward
cusps in their
, just as mode (a) does, as seen in Fig. 8c.
Presumably, the other modes higher up in the spectrum that possess downward
cusps in their 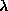 -dependences are also strongly affected by the vortex
instability.
-dependences are also strongly affected by the vortex
instability.
The crossover from in-plane to out-of-plane vortices exhibits itself in an even
more obvious way. A significant fraction of the modes are degenerate for
 , but all of these degeneracies split for
, but all of these degeneracies split for
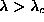 . These degeneracies must be associated with a symmetry
of the in-plane vortex, that is broken in the out-of-plane vortex. For
example, consider the lowest degenerate mode, (b), in Fig. 3b, for
. These degeneracies must be associated with a symmetry
of the in-plane vortex, that is broken in the out-of-plane vortex. For
example, consider the lowest degenerate mode, (b), in Fig. 3b, for
 . We might expect that a vortex in an infinite, continuum
limit system would have a degenerate pair of zero-frequency modes associated
with translation of its position in the two lattice directions. This pair
would then be shifted to finite frequency on the discrete lattice, and when the
vortex is additionally confined to a finite system as we have here, they would
correspond to the two different directions along which the vortex center
position could oscillate, rather than translate. But clearly, with this
interpretation there is some problem to understand how this spatial
symmetry could be broken in the out-of-plane vortex, or why the out-of-plane
vortex wouldn't have a degenerate pair of translation modes. On the other
hand, it is known that the dynamical response of the out-of-plane vortex to an
external force is substantially different from that for the in-plane vortex.
This is because the the gyrovector (vorticity times
. We might expect that a vortex in an infinite, continuum
limit system would have a degenerate pair of zero-frequency modes associated
with translation of its position in the two lattice directions. This pair
would then be shifted to finite frequency on the discrete lattice, and when the
vortex is additionally confined to a finite system as we have here, they would
correspond to the two different directions along which the vortex center
position could oscillate, rather than translate. But clearly, with this
interpretation there is some problem to understand how this spatial
symmetry could be broken in the out-of-plane vortex, or why the out-of-plane
vortex wouldn't have a degenerate pair of translation modes. On the other
hand, it is known that the dynamical response of the out-of-plane vortex to an
external force is substantially different from that for the in-plane vortex.
This is because the the gyrovector (vorticity times 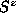 at vortex core)
of the in-plane vortex
is zero, but for the out-of-plane vortex it is nonzero [15].
However, one would still need to explain the additional symmetries associated
with the other degeneracies as well.
at vortex core)
of the in-plane vortex
is zero, but for the out-of-plane vortex it is nonzero [15].
However, one would still need to explain the additional symmetries associated
with the other degeneracies as well.
A simpler way to view the degeneracies is that they are most closely associated
with symmetries of the in-plane vortex in spin space, the most important
of which is that it is invariant under reversal of the out-of-plane component,
because that component is zero. Then, all of the degeneracies must
somehow be associated with the symmetry of those modes under reversal of their
out-of-plane spin components, 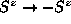 . For the in-plane
vortex, this is equivalent to
. For the in-plane
vortex, this is equivalent to 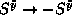 . Once
we have an out-of-plane vortex for
. Once
we have an out-of-plane vortex for 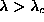 , the static vortex
structure has all
, the static vortex
structure has all 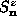 either greater than 0 or all
either greater than 0 or all 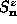 less than 0. Then it is clear that the perturbations (specifically,
less than 0. Then it is clear that the perturbations (specifically,
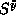 ) about that static structure cost different energies depending
on whether they increase or decrease each
) about that static structure cost different energies depending
on whether they increase or decrease each 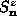 , leading to a
breaking of the up-down
, leading to a
breaking of the up-down 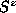 symmetry that was present in the in-plane
vortex. However, thinking this way, there is still a problem to understand
which of the modes would be in degenerate pairs for
symmetry that was present in the in-plane
vortex. However, thinking this way, there is still a problem to understand
which of the modes would be in degenerate pairs for
 .
.



Next: Complete Wavefunction Phase
Up: Discussion and Conclusions
Previous: Discussion and Conclusions
Gary M Wysin
Mon Sep 11 12:02:10 CDT 1995
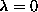 , there is not too much difference
in this mode's structure, regardless of the presence or absence of the vortex
[compare Fig. 7c and Fig. 10c], except that the mode is more
concentrated at the system center when the vortex is present. However, this
mode also concentrates itself additionally onto the vortex core for
, there is not too much difference
in this mode's structure, regardless of the presence or absence of the vortex
[compare Fig. 7c and Fig. 10c], except that the mode is more
concentrated at the system center when the vortex is present. However, this
mode also concentrates itself additionally onto the vortex core for 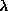 near
near 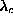 , just as mode (a) does, as seen in Fig. 8c.
Presumably, the other modes higher up in the spectrum that possess downward
cusps in their
, just as mode (a) does, as seen in Fig. 8c.
Presumably, the other modes higher up in the spectrum that possess downward
cusps in their 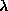 -dependences are also strongly affected by the vortex
instability.
-dependences are also strongly affected by the vortex
instability.
 , but all of these degeneracies split for
, but all of these degeneracies split for
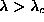 . These degeneracies must be associated with a symmetry
of the in-plane vortex, that is broken in the out-of-plane vortex. For
example, consider the lowest degenerate mode, (b), in Fig.
. These degeneracies must be associated with a symmetry
of the in-plane vortex, that is broken in the out-of-plane vortex. For
example, consider the lowest degenerate mode, (b), in Fig.  . We might expect that a vortex in an infinite, continuum
limit system would have a degenerate pair of zero-frequency modes associated
with translation of its position in the two lattice directions. This pair
would then be shifted to finite frequency on the discrete lattice, and when the
vortex is additionally confined to a finite system as we have here, they would
correspond to the two different directions along which the vortex center
position could oscillate, rather than translate. But clearly, with this
interpretation there is some problem to understand how this spatial
symmetry could be broken in the out-of-plane vortex, or why the out-of-plane
vortex wouldn't have a degenerate pair of translation modes. On the other
hand, it is known that the dynamical response of the out-of-plane vortex to an
external force is substantially different from that for the in-plane vortex.
This is because the the gyrovector (vorticity times
. We might expect that a vortex in an infinite, continuum
limit system would have a degenerate pair of zero-frequency modes associated
with translation of its position in the two lattice directions. This pair
would then be shifted to finite frequency on the discrete lattice, and when the
vortex is additionally confined to a finite system as we have here, they would
correspond to the two different directions along which the vortex center
position could oscillate, rather than translate. But clearly, with this
interpretation there is some problem to understand how this spatial
symmetry could be broken in the out-of-plane vortex, or why the out-of-plane
vortex wouldn't have a degenerate pair of translation modes. On the other
hand, it is known that the dynamical response of the out-of-plane vortex to an
external force is substantially different from that for the in-plane vortex.
This is because the the gyrovector (vorticity times 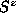 at vortex core)
of the in-plane vortex
is zero, but for the out-of-plane vortex it is nonzero [
at vortex core)
of the in-plane vortex
is zero, but for the out-of-plane vortex it is nonzero [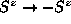 . For the in-plane
vortex, this is equivalent to
. For the in-plane
vortex, this is equivalent to 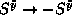 . Once
we have an out-of-plane vortex for
. Once
we have an out-of-plane vortex for 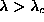 , the static vortex
structure has all
, the static vortex
structure has all 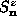 either greater than 0 or all
either greater than 0 or all 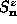 less than 0. Then it is clear that the perturbations (specifically,
less than 0. Then it is clear that the perturbations (specifically,
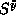 ) about that static structure cost different energies depending
on whether they increase or decrease each
) about that static structure cost different energies depending
on whether they increase or decrease each 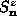 , leading to a
breaking of the up-down
, leading to a
breaking of the up-down 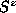 symmetry that was present in the in-plane
vortex. However, thinking this way, there is still a problem to understand
which of the modes would be in degenerate pairs for
symmetry that was present in the in-plane
vortex. However, thinking this way, there is still a problem to understand
which of the modes would be in degenerate pairs for
 .
.