|
Michael
J. O’Shea Belaying |
|
Special Feature: Extreme Physics ‘The most
dangerous point in a climb may be just after you start’, M. J. O’Shea, Physics Education Phys. Educ. 43
494-499 (2008) Climbing is a
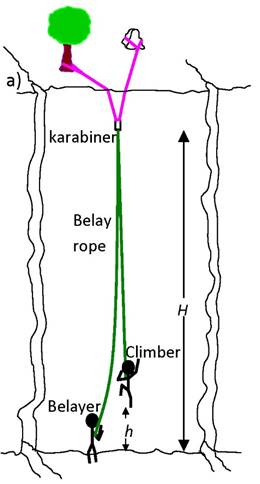
relatively safe sport due to the belay system used. The belay rope is a so-called dynamic rope
– it is able to stretch in response to a shock load. If the climber falls their fall is arrested
somewhat gently as the rope stretches and brings the climber to a stop. There are several important parameters
here: · the ability of the rope to stretch · the length of the rope played out · the amount of slack in the rope The length of rope and
the ability of the rope to stretch determine the spring constant k of the rope. With the above information and the mass of
the climber one can calculate the maximum force the rope will exert on the
climber during a fall. Should a climber slip
at the start of a climb, the rope may stretch enough that the climber may contact
the ground. Modeling this contact
allows an estimate of the force the climber experiences when they contact the
ground. As an
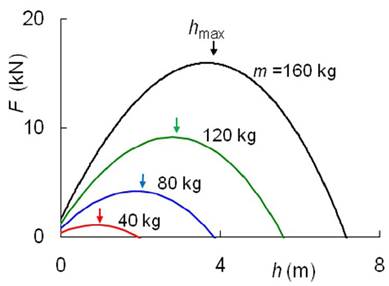
example consider the case where the spring constant per unit length is
14 kN, the climb height is H is 20
m, and as the climber lands they drop their weight a distance d of 0.20 m. The plot shows the force (average value)
experienced on landing as a function of fall heights h for various climber masses and this force show a maximum for
each mass. To model the rope as a spring, its
physics spring constant k must be
found. There is a problem that allows
you to do this here. A problem involving a climber who
falls and is caught by the rope before they hit the ground is here. A problem involving a special case
of this work (no tension or slack in the belay rope) can be found here. Details of the derivation of various equations of this work can be found here. |