Our Research

 

 

 

Home         KamLAND Experiment        Our Research          Results           About Me

 

           

     This research develops an empirical approximation of the appearance probability without assuming neutrino (or anti-neutrino) oscillations and takes into account most of the reactor distances.

 

Incorporating Multiple Reactor Distances

 

Number of Ep Counts equation: (For a derivation, look at the PowerPoint presentation attached in the Home page)

 

 

 

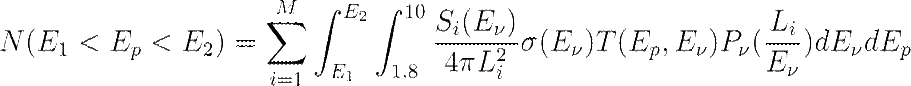
After a change of variables:

 

 

 

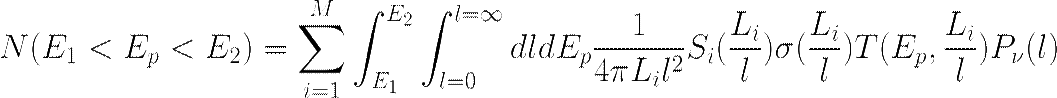
where,    N   =       

 

                                                                          Q   =     

 

 

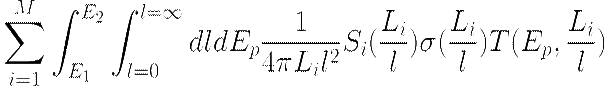
                                                                                                                                                                              P   =   

 

From this, we get:

 

After minimizing chi square, a way to invert the Q matrix is by:

 

 

 

 

Forming the Q matrix:

 

•      Test for l values ranging from 9-550 km per MeV

•      If the Eν lies between 1.8 MeV-10 MeV, then the values are plugged into the Q equation

•      If the Eν lies outside of that range, it does not contribute to the detector, so zero is inputted for that matrix element

•      Obtain a different Q matrix for each reactor

•      Superpose all the Q matrices

 

Binning:

 

     Why bin the Eps?

•      The greater the counts per bin, the smaller the relative error

     Why bin the l's?

•      More functions than unknowns

•      A higher sum in each l column will provide for a smaller error

 

Definitions:

 

•      Q0 = 76x1083 Q

•      P0 = 1083x1 (no oscillations)

•      N0 = 76x1

•      Q’0 = 17x11 binned Q0

•      N’0 = 17x1 binned N0

•      P1 = 1083x1 (using oscillation formula)

•      N1 = 76x1 (test N or real events data N)

•      N’1 =  17x1 binned N1

•      C is boxed

•      Y is what is outside the box in the same equation as C, excluding N and P

•      R is a matrix containing the orthonormal eigenvectors for each eigenvalue

•      D is a diagonal matrix containing all the eigenvalues of C

•      D tilde inverse has the smallest eigenvalue element equal to zero

 

 

The Test

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

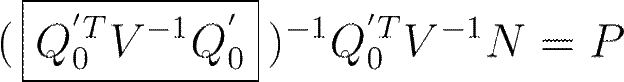
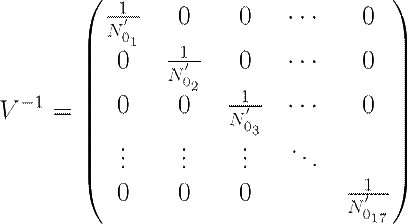
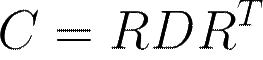
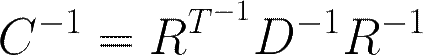
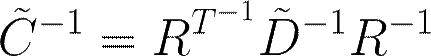
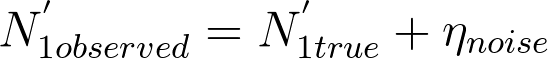
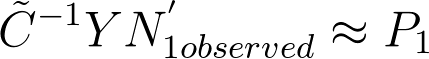
Why omit the smallest eigenvalue?

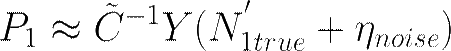
Hence, the smaller the eigenvalues get, the bigger the noise error gets

 

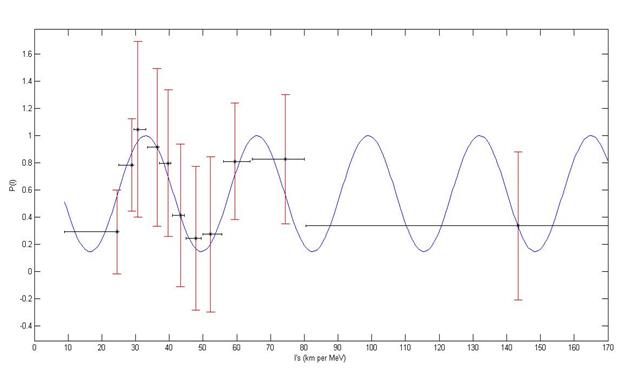
Average Estimated P(l) of the KamLAND Equation

 

This program is funded by the National Science Foundation through grant number PHY-1157044.  Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.