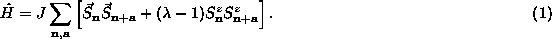
Consider the classical 2D-model of a Heisenberg easy-plane AFM, with the Hamiltonian
Here J > 0 is the exchange constant, 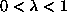 describes
anisotropy with the xy-plane as the easy-plane.
Spins
describes
anisotropy with the xy-plane as the easy-plane.
Spins 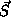 are classical vectors on a 2D-square lattice with lattice
constant a.
are classical vectors on a 2D-square lattice with lattice
constant a. 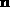 denotes lattice sites of one sublattice,
and
denotes lattice sites of one sublattice,
and  's are the set of displacements to the
nearest-neighbors on the other sublattice. We are interested in
the small anisotropy case
's are the set of displacements to the
nearest-neighbors on the other sublattice. We are interested in
the small anisotropy case 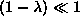 .
.
A continuum model of AFM's can be derived from (1) in
the usual way, see [2],[4],[6]. We
define the magnetization vector 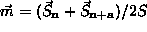 and the sublattice
magnetization vector
and the sublattice
magnetization vector 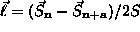 on the set of nearest-neighbor
pairs, with the constraints
on the set of nearest-neighbor
pairs, with the constraints 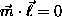 ,
, 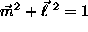 .
Then, for low frequencies
.
Then, for low frequencies 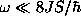 and small gradients,
and small gradients,
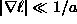 , the magnetization of an AFM is
small,
, the magnetization of an AFM is
small, 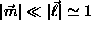 . The
magnetization can be considered as a ``slave'' variable, and can
be expressed as
. The
magnetization can be considered as a ``slave'' variable, and can
be expressed as 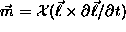 , where
, where 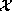 is a
susceptibility defined below [Eq. (3)]. After
eliminating
is a
susceptibility defined below [Eq. (3)]. After
eliminating 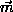 one obtains equations for
one obtains equations for 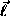 only.
Using the usual angular variables, (
only.
Using the usual angular variables, (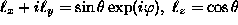 ) these equations can be
written in the form[4],[6]
) these equations can be
written in the form[4],[6]
where c is the magnon phase velocity, 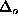 is
the characteristic length scale. For the Hamiltonian
(1)
is
the characteristic length scale. For the Hamiltonian
(1)