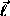 oscillating in the
easy-plane, and ``out-of-plane'' one with
oscillating in the
easy-plane, and ``out-of-plane'' one with 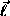 oscillating
in the z-direction, with out-of-plane and in-plane oscillations
of
oscillating
in the z-direction, with out-of-plane and in-plane oscillations
of 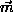 , respectively. These have gapless and finite
activation dispersion laws, respectively:
, respectively. These have gapless and finite
activation dispersion laws, respectively:
In the absence of
vortices, this 2D-model has well-known magnon excitations about
the classical AFM ground state. There are two branches of
magnons: ``in-plane'' one with 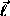 oscillating in the
easy-plane, and ``out-of-plane'' one with
oscillating in the
easy-plane, and ``out-of-plane'' one with 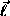 oscillating
in the z-direction, with out-of-plane and in-plane oscillations
of
oscillating
in the z-direction, with out-of-plane and in-plane oscillations
of 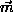 , respectively. These have gapless and finite
activation dispersion laws, respectively:
, respectively. These have gapless and finite
activation dispersion laws, respectively:
where 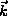 is the wave vector. These can be also
obtained from a Taylor expansion of the dispersion law for the
discrete model, see Ref. [13].
is the wave vector. These can be also
obtained from a Taylor expansion of the dispersion law for the
discrete model, see Ref. [13].
In the continuum models like Eq. (2), the
out-of-plane vortex with the usual topological charges of
vorticity  and polarization p is described by the
solution[14]
and polarization p is described by the
solution[14] 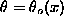 ,
, 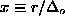 ,
, 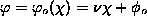 , where
, where
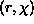 are polar coordinates,
are polar coordinates, 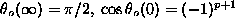 , and
, and 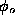 is a constant. Only
the case
is a constant. Only
the case 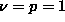 will be discussed here. The function
will be discussed here. The function
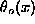 is described by an ordinary differential equation
(ODE) which can be solved numerically by a shooting method, see
[14],[15].
is described by an ordinary differential equation
(ODE) which can be solved numerically by a shooting method, see
[14],[15].
The distribution of spins in the static vortex also can be
analyzed directly from the discrete model (1), see
[10],[11]. Energy minimization is carried out
starting from a nearly in-plane structure, and redirecting spins
along the effective fields due to the neighbors, iterating until
convergence. The coincidence between the data of these approaches
is surprisingly good, even for large anisotropy, see Fig. 1.
Large discrepancies appear only for 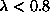 \
(
\
(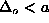 ), when the vortex structure is rapidly
approaching the in-plane form.
), when the vortex structure is rapidly
approaching the in-plane form.