


Next: The Model.
Up: Normal Modes and Soliton
Previous: Normal Modes and Soliton
It is well-known that strongly nonlinear topologically nontrivial
excitations (solitons) play a special role in low-dimensional
magnetic systems. For example, kinks in 1D systems are
responsible for the destruction of long-range order at finite
temperatures, and the presence of vortices in 2D systems gives
rise to a special type of phase transition -- the
Berezinskii-Kosterlitz-Thouless transition[1].
Experimental observation of soliton signatures in the response
functions is usually based on the fact that translational motion
of solitons leads to the the so-called soliton central peak, for
review see [2],[3],[4]. Another
possibility is to look for internal degrees of freedom of
solitons, such as magnon modes localized on a soliton.
Resonances at characteristic frequencies of an internal motion
can be observed in electron spin resonance or inelastic neutron
scattering (INS) experiments. In 1D such effects of ``soliton
magnetic resonance'' were detected in the Ising-type
antiferromagnet (AFM) CsCoCl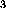 [5], and were
predicted theoretically for Heisenberg AFMs [6]. In
3D, magnon modes localized on domain walls in AFMs were observed
in thulium orthoferrite [7]. Presently, no
experimentally testable examples of internal soliton dynamics in
2D are known. Moreover, only a quasi-local mode has been
predicted for solitons in isotropic [8],
XY-type[9], and easy-plane
Heisenberg[10],[11],[12] 2D ferromagnets
(FM).
[5], and were
predicted theoretically for Heisenberg AFMs [6]. In
3D, magnon modes localized on domain walls in AFMs were observed
in thulium orthoferrite [7]. Presently, no
experimentally testable examples of internal soliton dynamics in
2D are known. Moreover, only a quasi-local mode has been
predicted for solitons in isotropic [8],
XY-type[9], and easy-plane
Heisenberg[10],[11],[12] 2D ferromagnets
(FM).
The aim of the present Letter is to draw attention to the fact
that in classical easy-plane Heisenberg 2D AFMs ``out-of-plane''
vortices have finite-frequency truly localized internal
modes which may be detectable in resonance or INS experiments. We
also numerically obtain the vortex-magnon S-matrix in the
long-wavelength region, analyzing linearized perturbations of the
vortex structure, for continuum and discrete lattice models.
Gary M Wysin
Wed Sep 6 18:51:57 CDT 1995
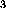 [5], and were
predicted theoretically for Heisenberg AFMs [6]. In
3D, magnon modes localized on domain walls in AFMs were observed
in thulium orthoferrite [7]. Presently, no
experimentally testable examples of internal soliton dynamics in
2D are known. Moreover, only a quasi-local mode has been
predicted for solitons in isotropic [8],
XY-type[9], and easy-plane
Heisenberg[10],[11],[12] 2D ferromagnets
(FM).
[5], and were
predicted theoretically for Heisenberg AFMs [6]. In
3D, magnon modes localized on domain walls in AFMs were observed
in thulium orthoferrite [7]. Presently, no
experimentally testable examples of internal soliton dynamics in
2D are known. Moreover, only a quasi-local mode has been
predicted for solitons in isotropic [8],
XY-type[9], and easy-plane
Heisenberg[10],[11],[12] 2D ferromagnets
(FM).