


Next: Results.
Up: Lifetime of vortices in
Previous: The Model.
We studied classical spins on a square 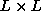 lattice,
for L= 16, 32 and 64, with periodic boundary conditions.
The simulation was a combination of Monte Carlo and spin-dynamics methods
applied to Hamiltonian (2.1).
We used the Metropolis Monte Carlo method to produce initial spin
configurations (IC) at a given temperature
lattice,
for L= 16, 32 and 64, with periodic boundary conditions.
The simulation was a combination of Monte Carlo and spin-dynamics methods
applied to Hamiltonian (2.1).
We used the Metropolis Monte Carlo method to produce initial spin
configurations (IC) at a given temperature 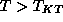 ,
but close to
,
but close to 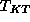 .
Then, each initial configuration was evolved in time using the equations of
motion for the spins.
We accumulated statistics of the fluctuating number of free vortices during
the time evolution to determine the free vortex lifetime.
A vortex in a given unit cell is considered free if there are no vortices or
antivortices in any of the 8 surrounding unit cells.
.
Then, each initial configuration was evolved in time using the equations of
motion for the spins.
We accumulated statistics of the fluctuating number of free vortices during
the time evolution to determine the free vortex lifetime.
A vortex in a given unit cell is considered free if there are no vortices or
antivortices in any of the 8 surrounding unit cells.
In the Monte Carlo, we used the first 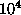 Monte Carlo steps (MCS) for equilibration, writing data
after each 500 or 1000 MCS. Individual spins were updated
by adding increments in arbitrary directions, and then renormalizing
to unit lengths.
We generated between 25 and 100 IC at each temperature, so that
the relative error in
Monte Carlo steps (MCS) for equilibration, writing data
after each 500 or 1000 MCS. Individual spins were updated
by adding increments in arbitrary directions, and then renormalizing
to unit lengths.
We generated between 25 and 100 IC at each temperature, so that
the relative error in 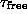 is 1 to 3 percent.
is 1 to 3 percent.
The time evolution simulation solves numerically the
Landau---Lifshitz spin equations of motion[12],
using a fourth order Runge---Kutta scheme.
The free vortex lifetime was determined
during the time evolution simulation.
The number of free vortices was counted at each time step and the times
of its decrements were recorded.
If 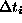 is the time between the
is the time between the 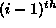 and
and 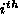 decrements,
decrements,
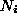 is the number of free vortices (plus antivortices) in the system before the
is the number of free vortices (plus antivortices) in the system before the 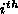 decrement, and
decrement, and 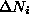 is the change of
is the change of 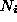 , then
from this event the estimate of the vortex lifetime
from the time interval
, then
from this event the estimate of the vortex lifetime
from the time interval 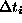 is
is

The denominator introduces a weighting factor that reduces the importance of
fluctuations involving a change in 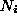 of more than one.
This formula gives correct results if
of more than one.
This formula gives correct results if 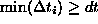 , where
dt is the integration time step. Also, this condition assures that most of
the fluctuations and the processes which occur will change
, where
dt is the integration time step. Also, this condition assures that most of
the fluctuations and the processes which occur will change 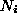 by one
or two.
[
by one
or two.
[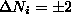 for vortex pair creation/annihilation,
for vortex pair creation/annihilation, 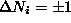 when a vortex changes from bound to free or vice-versa.]
The choice of the time step dt depends on T and L.
Increasing either of these increases the average number of vortices,
and diminishes the time scale over which their numbers fluctuate, and
requires a decrease of dt. The smallest dt we used was
when a vortex changes from bound to free or vice-versa.]
The choice of the time step dt depends on T and L.
Increasing either of these increases the average number of vortices,
and diminishes the time scale over which their numbers fluctuate, and
requires a decrease of dt. The smallest dt we used was
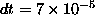 for a
for a 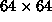 system at temperature
system at temperature 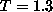 .
In order to check the reliability of the simulations with small time
steps we compared the components of the
spins(
.
In order to check the reliability of the simulations with small time
steps we compared the components of the
spins(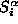 ,
, 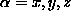 ) with precision
) with precision
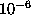 at equal times for runs with
at equal times for runs with 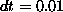 and
and 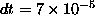 out to a final time
out to a final time 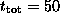 , finding no differences.
, finding no differences.
We also considered the free-vortex number-number time correlation function,
as another way to obtain the time scale of the vortex number fluctuations,
and as a check of the lifetime measurement.
The definition is

where 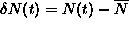 is the instantaneous deviation in
is the instantaneous deviation in
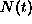 from its time-independent average,
from its time-independent average, 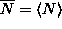 .
.
Under the phenomenological assumption of linear response,
if the number of free vortices deviates slightly from the equilibrium number
at a given temperature, then the rate at which the system relaxes back to
equilibrium is proportional to the deviation from equilibrium.
If it is valid, it leads to a relaxation time 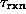 ;
;

For the simulations of the correlation function we used 40
initial configurations and a time step 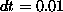 for all
temperatures. Each IC was integrated in time up to
for all
temperatures. Each IC was integrated in time up to
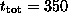 .
Each
.
Each 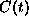 point is from approximately 300
measurements since we constrained the argument of
point is from approximately 300
measurements since we constrained the argument of 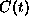 in the
interval
in the
interval 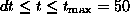 (
(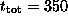 ).
The successive measurements for a given IC and time t in Eq. (3.2)
were taken with a shift of 1.0 time unit in order to minimize the
correlation of the data.
The final data points were obtained using a weighted average[13]
over the initial configurations.
).
The successive measurements for a given IC and time t in Eq. (3.2)
were taken with a shift of 1.0 time unit in order to minimize the
correlation of the data.
The final data points were obtained using a weighted average[13]
over the initial configurations.



Next: Results.
Up: Lifetime of vortices in
Previous: The Model.
Gary M Wysin
Fri Sep 1 16:26:33 CDT 1995
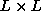 lattice,
for L= 16, 32 and 64, with periodic boundary conditions.
The simulation was a combination of Monte Carlo and spin-dynamics methods
applied to Hamiltonian (2.1).
We used the Metropolis Monte Carlo method to produce initial spin
configurations (IC) at a given temperature
lattice,
for L= 16, 32 and 64, with periodic boundary conditions.
The simulation was a combination of Monte Carlo and spin-dynamics methods
applied to Hamiltonian (2.1).
We used the Metropolis Monte Carlo method to produce initial spin
configurations (IC) at a given temperature 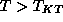 ,
but close to
,
but close to 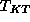 .
Then, each initial configuration was evolved in time using the equations of
motion for the spins.
We accumulated statistics of the fluctuating number of free vortices during
the time evolution to determine the free vortex lifetime.
A vortex in a given unit cell is considered free if there are no vortices or
antivortices in any of the 8 surrounding unit cells.
.
Then, each initial configuration was evolved in time using the equations of
motion for the spins.
We accumulated statistics of the fluctuating number of free vortices during
the time evolution to determine the free vortex lifetime.
A vortex in a given unit cell is considered free if there are no vortices or
antivortices in any of the 8 surrounding unit cells.
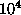 Monte Carlo steps (MCS) for equilibration, writing data
after each 500 or 1000 MCS. Individual spins were updated
by adding increments in arbitrary directions, and then renormalizing
to unit lengths.
We generated between 25 and 100 IC at each temperature, so that
the relative error in
Monte Carlo steps (MCS) for equilibration, writing data
after each 500 or 1000 MCS. Individual spins were updated
by adding increments in arbitrary directions, and then renormalizing
to unit lengths.
We generated between 25 and 100 IC at each temperature, so that
the relative error in 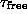 is 1 to 3 percent.
is 1 to 3 percent.
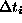 is the time between the
is the time between the 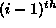 and
and 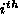 decrements,
decrements,
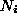 is the number of free vortices (plus antivortices) in the system before the
is the number of free vortices (plus antivortices) in the system before the 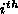 decrement, and
decrement, and 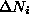 is the change of
is the change of 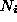 , then
from this event the estimate of the vortex lifetime
from the time interval
, then
from this event the estimate of the vortex lifetime
from the time interval 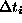 is
is

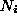 of more than one.
This formula gives correct results if
of more than one.
This formula gives correct results if 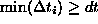 , where
dt is the integration time step. Also, this condition assures that most of
the fluctuations and the processes which occur will change
, where
dt is the integration time step. Also, this condition assures that most of
the fluctuations and the processes which occur will change 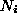 by one
or two.
[
by one
or two.
[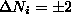 for vortex pair creation/annihilation,
for vortex pair creation/annihilation, 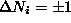 when a vortex changes from bound to free or vice-versa.]
The choice of the time step dt depends on T and L.
Increasing either of these increases the average number of vortices,
and diminishes the time scale over which their numbers fluctuate, and
requires a decrease of dt. The smallest dt we used was
when a vortex changes from bound to free or vice-versa.]
The choice of the time step dt depends on T and L.
Increasing either of these increases the average number of vortices,
and diminishes the time scale over which their numbers fluctuate, and
requires a decrease of dt. The smallest dt we used was
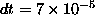 for a
for a 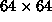 system at temperature
system at temperature 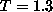 .
In order to check the reliability of the simulations with small time
steps we compared the components of the
spins(
.
In order to check the reliability of the simulations with small time
steps we compared the components of the
spins(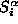 ,
, 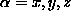 ) with precision
) with precision
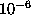 at equal times for runs with
at equal times for runs with 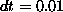 and
and 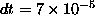 out to a final time
out to a final time 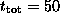 , finding no differences.
, finding no differences.

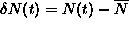 is the instantaneous deviation in
is the instantaneous deviation in
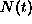 from its time-independent average,
from its time-independent average, 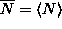 .
.
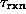 ;
;

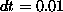 for all
temperatures. Each IC was integrated in time up to
for all
temperatures. Each IC was integrated in time up to
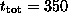 .
Each
.
Each 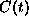 point is from approximately 300
measurements since we constrained the argument of
point is from approximately 300
measurements since we constrained the argument of 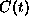 in the
interval
in the
interval 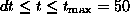 (
(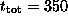 ).
The successive measurements for a given IC and time t in Eq. (
).
The successive measurements for a given IC and time t in Eq. (