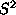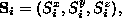
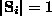We consider a system of classical spins on the sphere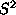 
(
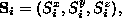
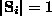), interacting
on a 2D square lattice.
The Hamiltonian is
where the sum is over nearest-neighbor lattice sites, J > 0 determines
ferromagnetic coupling and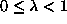 
introduces
easy-plane anisotropy.
There are two types of static vortices which arise in this
model--- out-of-plane and in-plane ones, depending on the
presence or absence respectively of nonzero out-of-plane spin
components (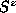
),
with identical in-plane spin structure.
A study of their static properties[9],[10],[11]
shows that their stability depends on the
anisotropy parameter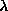 
.
Below a specific value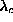 
(
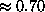for square lattice)
only the in-plane vortex is stable
while for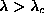 
only the out-of-plane one is stable.
Because the out-of-plane structure may influence the vortex interactions
and therefore their lifetime, we consider both 
and
.
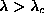Assuming an ideal gas of free vortices with infinite lifetime,
Mertens et al.[8] obtained the asymptotic behavior for
the in-plane correlation function
:
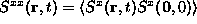The characteristic time implied by this equation is
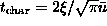, which is approximately the time for
a vortex to move one correlation length.
Thus, the theory is reasonable provided the vortex lifetime is at least
that long.
For an order of magnitude result the characteristic time is
approximately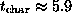 
from the estimates[8]
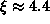and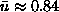 
at temperature 
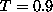(length is
in lattice constant units, T in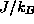 
, and time in 
).
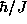We use this value to compare with the lifetime we obtain from our
simulation at this particular temperature.
The space-time Fourier transformation of Eq. (2.2) leads to a squared Lorentzian central peak form[8]
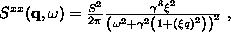
where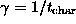 
,
with a wavevector-dependent characteristic
frequency width
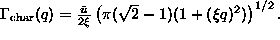
However, a finite vortex lifetime will lead to fluctuations in the number
of free vortices on a length scale of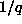 
of the order of 
,
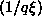with frequency higher than the inverse vortex lifetime,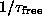 
.
Thus,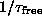 
will represent a cutoff frequency below which the
ideal vortex gas theory for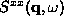 
cannot be a
valid description.
As mentioned above, the two types of static vortices
have the same xy behavior of their spin components but different
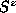components.
For 
, there is no contribution to
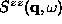from
static in-plane vortices and the vortex contribution can only be from
moving vortices.
On the other hand, for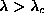 
, the main contribution
can be from static (out-of-plane) vortex structures.
In either case, the ideal gas theory predicts a central peak
in Fourier space, but with a Gaussian shape for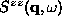 
rather than the squared Lorentzian for the
in-plane correlation function.
Since for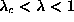 
,
the theory for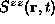 
may be built in first approximation
by assuming that the out-of-plane structure of a moving vortex can be
approximated by the static structure[8],
it is important to compare the vortex lifetime in this case with the case
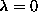, where the spin-wave peak is strongly softened
and the central peak can be clearly attributed to the motion of vortices.
