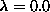As a preliminary step we made a Monte Carlo
finite-size scaling[14] study
to determine accurately the KT-temperature, for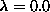 
, since
the precise critical point for this model is not known.
Using L= 10, 20, 40 and 80, and averaging over 160,000 states at
each temperature, we calculated the reduced fourth-order cumulant,
where M is the total in-plane magnetic moment.
This definition is appropriate for systems with XY symmetry, with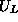 
approaching 0.5 in the low-temperature phase and 0.0 in the high-temperature
phase. The result is shown in Fig. 1; the curves for different L cross
at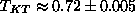 
. This is consistent with
the prediction of Menezes et al.[15] [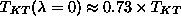
(planar rotator)], combined with the
MC calculations of Gupta et al.[16] [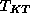
(planar rotator)
], although the Menezes et al. theory does not give the correct
for either model.
On this basis, to have enough vortices for lifetime measurements, we considered the
temperature range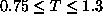 
with a step 
.
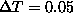We obtained the free vortex lifetime for two values of the anisotropy
parameter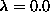 
and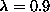 
, as shown in
Figure 2 for system sizes L=32, 64.
The lifetime decreases starting from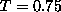 
and it is close to saturation
when approaching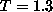 
.
The data points for 
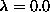are higher than those for 
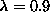for all T studied.
For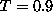 
and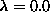 
, we have 
,
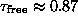whereas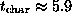 
(see Sec. ii).
This implies a cutoff frequency 
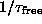several times greater than
the characteristic frequency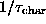 
in the Mertens
et al.[8] theory.
For comparison, some typical results for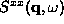 
from an L=100 system are shown in Fig. 3, for 
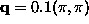. The observed CP is strong for higher temperatures, and for
frequencies well below our measured values of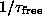 
.
This implies that the ideal vortex gas description
for frequencies below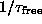 
is inappropriate.
The lifetime does not show dependence on the size of the system for
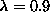; the data points for 
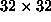and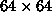 
overlap within their error bars.
On the contrary, there is a pronounced finite size effect when approaching the
critical region from above for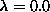 
.
This indicates that the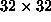 
system size is too small to be used to
study the bulk properties, unless some finite size scaling is applied in
a domain close enough to the critical temperature.
The presence of this finite size effect and its absence for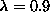 
is because the correlation length for 
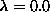is greater than that
for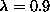 
for the corresponding temperatures, since
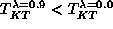[15].
In Fig. 4 we show the free vortex number---number
correlation function for temperatures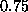 
, 
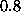, and 
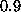, for
.
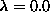As expected, the correlation function decays faster and decorrelates at
earlier times for larger temperature.
The correlation function
cannot be described by linear response theory, implying that
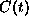is not governed by a single time scale.
This is also confirmed by the tails of these curves.
For example, for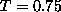 
, a linear fit to 
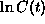from the first 4--5 points
gives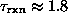 
. However 
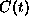decorrelates at large times
t>40, which contradicts the simple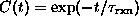 
behavior.
On the other hand, relaxation times determined from the small-t linear fits
are of the same order of magnitude and have the same behavior with temperature
as 
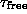determined above.
Similar results for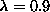 
show a faster decay of 
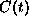than for
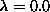, completely in agreement with our measurements of
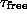for both values of 
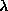, however, at large times
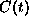decorrelates slightly slower than for the case 
.
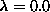