


Next: The Model.
Up: Lifetime of vortices in
Previous: Lifetime of vortices in
It is well known [1] that in two-dimensional (2D) systems with
continuous symmetry there is no long range order:
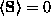 for
all temperatures, where
for
all temperatures, where 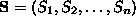 and
and 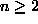 .
But for continuous Abelian symmetry, a finite-temperature
topological phase transition exists[2] and
occurs through unbinding of topological point defects[3].
These systems include superfluids[4],
2D crystalline
solids[5], and XY magnets[2].
.
But for continuous Abelian symmetry, a finite-temperature
topological phase transition exists[2] and
occurs through unbinding of topological point defects[3].
These systems include superfluids[4],
2D crystalline
solids[5], and XY magnets[2].
While the static thermodynamic properties are well described by the
Kosterlitz--Thouless theory[3], the dynamical properties are not so
well understood. There are variety of quasi-2D magnetic
materials, such as 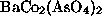 ,
,
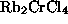 , and others[6],
where the dynamical properties were tested at low frequencies and long
wavelengths using inelastic neutron-scattering measurements.
More recent experiments[7] show some deviations from
existing theories and Monte Carlo simulations.
Mertens et al.[8] built a theory which accounts
qualitatively well for the behavior of the dynamical form factor above
the transition temperature for both the in-plane and out-of-plane
correlations. The theory assumes an ideal gas of unbound vortices above
the Kosterlitz--Thouless transition temperature
, and others[6],
where the dynamical properties were tested at low frequencies and long
wavelengths using inelastic neutron-scattering measurements.
More recent experiments[7] show some deviations from
existing theories and Monte Carlo simulations.
Mertens et al.[8] built a theory which accounts
qualitatively well for the behavior of the dynamical form factor above
the transition temperature for both the in-plane and out-of-plane
correlations. The theory assumes an ideal gas of unbound vortices above
the Kosterlitz--Thouless transition temperature 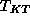 and it has as
adjustable parameters the root-mean-square vortex velocity
and it has as
adjustable parameters the root-mean-square vortex velocity
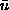 and the mean vortex-vortex separation
and the mean vortex-vortex separation 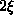 , where
, where 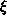 is the
correlation length.
The validity of this theory may depend on the lifetime of free vortices.
Though the ideal gas theory supposes infinite
lifetime, it will remain approximately correct for a dilute gas too,
if the lifetime
is the
correlation length.
The validity of this theory may depend on the lifetime of free vortices.
Though the ideal gas theory supposes infinite
lifetime, it will remain approximately correct for a dilute gas too,
if the lifetime 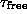 is greater than the characteristic
time which describes their motion
is greater than the characteristic
time which describes their motion 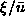 .
.
The purpose of this Letter is to investigate the free vortex lifetime,
for which there is no theory,
and to consider its implications for the ideal vortex gas theory.
The finite lifetime we measure also suggests that creation and
annihilation processes may make substantial contributions to
dynamic correlations.
Gary M Wysin
Fri Sep 1 16:26:33 CDT 1995
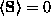 for
all temperatures, where
for
all temperatures, where 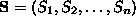 and
and 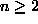 .
But for continuous Abelian symmetry, a finite-temperature
topological phase transition exists[2] and
occurs through unbinding of topological point defects[3].
These systems include superfluids[4],
2D crystalline
solids[5], and XY magnets[2].
.
But for continuous Abelian symmetry, a finite-temperature
topological phase transition exists[2] and
occurs through unbinding of topological point defects[3].
These systems include superfluids[4],
2D crystalline
solids[5], and XY magnets[2].
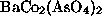 ,
,
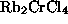 , and others[
, and others[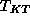 and it has as
adjustable parameters the root-mean-square vortex velocity
and it has as
adjustable parameters the root-mean-square vortex velocity
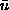 and the mean vortex-vortex separation
and the mean vortex-vortex separation 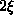 , where
, where 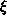 is the
correlation length.
The validity of this theory may depend on the lifetime of free vortices.
Though the ideal gas theory supposes infinite
lifetime, it will remain approximately correct for a dilute gas too,
if the lifetime
is the
correlation length.
The validity of this theory may depend on the lifetime of free vortices.
Though the ideal gas theory supposes infinite
lifetime, it will remain approximately correct for a dilute gas too,
if the lifetime 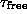 is greater than the characteristic
time which describes their motion
is greater than the characteristic
time which describes their motion 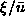 .
.