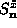 and
and 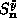 in terms of
the normal modes
in terms of
the normal modes 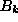 and
and 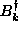 . This means we need to invert
the defining relations (2.12). First of all, the overall normalization
of
. This means we need to invert
the defining relations (2.12). First of all, the overall normalization
of 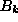 and
and 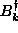 must be chosen so that their commutator is
unity,
must be chosen so that their commutator is
unity, 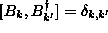 .
From the definitions, we must require
.
From the definitions, we must require
The complete eigenspectrum will contain all the information needed to determine
the expectation values and fluctuations of the individual spins in the system,
either for a single spinwave mode, or, for the system in thermal equilibrium.
To determine expectation values of the spin components or their squares, we
need to know 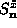 and
and 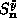 in terms of
the normal modes
in terms of
the normal modes 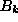 and
and 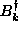 . This means we need to invert
the defining relations (2.12). First of all, the overall normalization
of
. This means we need to invert
the defining relations (2.12). First of all, the overall normalization
of 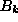 and
and 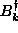 must be chosen so that their commutator is
unity,
must be chosen so that their commutator is
unity, 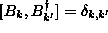 .
From the definitions, we must require
.
From the definitions, we must require
where 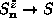 was used. We assume in what follows
that the
was used. We assume in what follows
that the 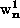 and
and 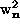 coefficients are now
rescaled to give the unit normalization and unit commutator of
coefficients are now
rescaled to give the unit normalization and unit commutator of 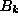 with
with
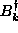 in Eq. (3.1). Then, the following inverse expressions
are assumed,
in Eq. (3.1). Then, the following inverse expressions
are assumed,
To determine the new coefficients 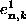 and
and 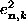 in terms of the
in terms of the 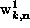 and
and 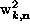 coefficients,
one can form the commutator of
coefficients,
one can form the commutator of 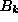 or
or 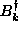 [Eqs. (2.12)] with
[Eqs. (2.12)] with
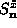 and with
and with 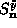 , giving
, giving
On the other hand, forming the commutator of 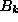 and
and 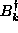 with
with 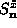 and
and 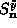 [Eq. (3.2)]
leads to equivalent results,
[Eq. (3.2)]
leads to equivalent results,
Thus there is the conversion between the coefficients;
As an application of these results, we can determine the
local magnetization for a site by finding an expectation value of the
original lab frame spin components, to quadratic order in the creation
and annihilation operators. In order to do this, we first need
expectation values of the spin components in the tilde coordinate system.
From their definitions, 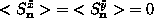 , because these are linear in
, because these are linear in 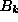 and
and
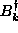 . However, the
. However, the  component will be reduced slightly
below S due to spin fluctuations of the modes. In order to preserve the
overall spin length and the commutation relations of
component will be reduced slightly
below S due to spin fluctuations of the modes. In order to preserve the
overall spin length and the commutation relations of 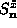 and
and  with
with 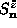 , it is necessary to
use the following expression for
, it is necessary to
use the following expression for 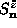 (as in the standard
Holstein-Primakoff [26] transformation):
(as in the standard
Holstein-Primakoff [26] transformation):
where the latter terms are the spin lowering and raising operators. Using Eq. (3.2) and Eq. (3.5), the expectation value of this expression is
where terms linear in the 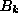 and
and 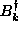 operators and terms
like
operators and terms
like 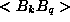 and
and 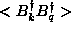 are zero in the
unperturbed (single-vortex) state and in single-quantum states and therefore
do not appear here.
The expectation values of the
are zero in the
unperturbed (single-vortex) state and in single-quantum states and therefore
do not appear here.
The expectation values of the 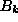 and
and 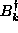 operators
will be determined by the type of state, whether it be a state with one
mode excited or a thermodynamic ensemble of states (equilibrium state).
For example, if the state that we are perturbing from
(single vortex) is denoted |0>, then single-quantum
excited states are denoted, |k>,
operators
will be determined by the type of state, whether it be a state with one
mode excited or a thermodynamic ensemble of states (equilibrium state).
For example, if the state that we are perturbing from
(single vortex) is denoted |0>, then single-quantum
excited states are denoted, |k>,
The fundamental expectation values are 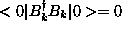 ,
and
,
and 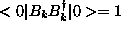 . On the other hand, if the
interest is in a thermal ensemble, then the expectation value required
will be the Bose-Einstein occupation,
. On the other hand, if the
interest is in a thermal ensemble, then the expectation value required
will be the Bose-Einstein occupation, 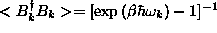 , where
, where 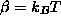 is the inverse
temperature. It is clear that the expectation values of the
is the inverse
temperature. It is clear that the expectation values of the
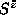 components will be less than S as a result of fluctuations,
while the expectation values of
components will be less than S as a result of fluctuations,
while the expectation values of 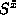 and
and 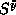 will be zero. As a result, it is straightforward to use Eq. (3.7) in the
coordinate transformation Eq. (2.6) to obtain the expectation values in the
original lab coordinates, i.e., the spin is just reduced in effective length,
will be zero. As a result, it is straightforward to use Eq. (3.7) in the
coordinate transformation Eq. (2.6) to obtain the expectation values in the
original lab coordinates, i.e., the spin is just reduced in effective length,
We also want to know the spin fluctuations associated with some state. The spin fluctuations will be defined in terms of squares of Cartesian spin components, relative to the vortex state. For instance, the in-plane and out-of-plane spin fluctuations are described by
Using the definitions of the tilde coordinates, Eq. (2.6), these are equivalent to
Making use of the expansion of spin components in the operators
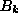 and
and 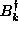 , Eq. (3.2), together with Eq. (3.5),
one can write the fluctuations in the tilde coordinates,
, Eq. (3.2), together with Eq. (3.5),
one can write the fluctuations in the tilde coordinates,
Finally, the resulting in-plane and out-of-plane fluctuations are: