


Next: RESULTS: SQUARE LATTICE
Up: NORMAL MODES OF VORTICES
Previous: NORMALIZATIONSPIN EXPECTATIONS
First, for a given value of 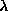 , the static vortex structure was found
using the relaxation procedure described in Section ii. This static
structure acquires nonzero out-of-plane spin components for
, the static vortex structure was found
using the relaxation procedure described in Section ii. This static
structure acquires nonzero out-of-plane spin components for
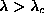 . Then, the eigenvalue problem [Eq. (2.14)] was
solved numerically for the eigenvectors and corresponding eigenvalues, for
systems with hundreds of sites. Because there are two variables per site, the
size of the matrix to diagonalize is
. Then, the eigenvalue problem [Eq. (2.14)] was
solved numerically for the eigenvectors and corresponding eigenvalues, for
systems with hundreds of sites. Because there are two variables per site, the
size of the matrix to diagonalize is 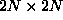 , where N is the number of
sites in the lattice. Calculations were performed for approximately circular
shaped systems, with the vortex centered in the system. For these finite
systems, there is a choice of either a free boundary condition or a fixed
boundary condition. For the free boundary condition, the lattice is cut off
along a circular boundary, and then the sites on the edge of the system simply
have a lower coordination number than those in the interior, and have a lower
effective stiffness as a result. For the fixed boundary condition, the set of
spins on the boundary of the system is coupled to an extra set of spins that
are outside the system, still on the same lattice, but held fixed in the
directions that the static in-plane vortex would give them. In this way, even
the spins at the edge of the system have the same coordination number as those
in the interior, however, they are coupled to spins that do not move that are
outside the system. Therefore, this fixed boundary condition, which is stiffer
than the free boundary condition, tends to give higher eigenfrequencies.
Additionally, the fixed boundary condition results in values for
, where N is the number of
sites in the lattice. Calculations were performed for approximately circular
shaped systems, with the vortex centered in the system. For these finite
systems, there is a choice of either a free boundary condition or a fixed
boundary condition. For the free boundary condition, the lattice is cut off
along a circular boundary, and then the sites on the edge of the system simply
have a lower coordination number than those in the interior, and have a lower
effective stiffness as a result. For the fixed boundary condition, the set of
spins on the boundary of the system is coupled to an extra set of spins that
are outside the system, still on the same lattice, but held fixed in the
directions that the static in-plane vortex would give them. In this way, even
the spins at the edge of the system have the same coordination number as those
in the interior, however, they are coupled to spins that do not move that are
outside the system. Therefore, this fixed boundary condition, which is stiffer
than the free boundary condition, tends to give higher eigenfrequencies.
Additionally, the fixed boundary condition results in values for 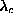 that converge faster to a limit with increasing system size, and for this
reason, most of the results reported here were produced with fixed boundary
conditions.
that converge faster to a limit with increasing system size, and for this
reason, most of the results reported here were produced with fixed boundary
conditions.
For a given system, the eigenspectrum was determined for a sequence of closely
spaced values of 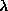 between 0 and 1. An eigenvector for one value of
between 0 and 1. An eigenvector for one value of
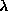 was projected onto the eigenvectors for the previous value of
was projected onto the eigenvectors for the previous value of
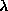 , and then identified with the one with which the overlap was the
greatest. This allowed the eigenfrequencies for the different modes to be
tracked as a function of
, and then identified with the one with which the overlap was the
greatest. This allowed the eigenfrequencies for the different modes to be
tracked as a function of 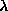 . For a system with N sites, N modes of
positive frequency, corresponding to the
. For a system with N sites, N modes of
positive frequency, corresponding to the 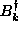 operators, resulted,
along with an equivalent set of N modes of negative frequency, corresponding
to the conjugate
operators, resulted,
along with an equivalent set of N modes of negative frequency, corresponding
to the conjugate 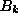 operators. Double precision was used so that
degenerate pairs of eigenmodes could be unambiguously identified, a necessity
for performing the eigenvector overlaps.
operators. Double precision was used so that
degenerate pairs of eigenmodes could be unambiguously identified, a necessity
for performing the eigenvector overlaps.



Next: RESULTS: SQUARE LATTICE
Up: NORMAL MODES OF VORTICES
Previous: NORMALIZATIONSPIN EXPECTATIONS
Gary M Wysin
Mon Sep 11 12:02:10 CDT 1995
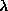 between 0 and 1. An eigenvector for one value of
between 0 and 1. An eigenvector for one value of
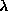 was projected onto the eigenvectors for the previous value of
was projected onto the eigenvectors for the previous value of
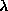 , and then identified with the one with which the overlap was the
greatest. This allowed the eigenfrequencies for the different modes to be
tracked as a function of
, and then identified with the one with which the overlap was the
greatest. This allowed the eigenfrequencies for the different modes to be
tracked as a function of 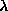 . For a system with N sites, N modes of
positive frequency, corresponding to the
. For a system with N sites, N modes of
positive frequency, corresponding to the 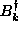 operators, resulted,
along with an equivalent set of N modes of negative frequency, corresponding
to the conjugate
operators, resulted,
along with an equivalent set of N modes of negative frequency, corresponding
to the conjugate 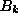 operators. Double precision was used so that
degenerate pairs of eigenmodes could be unambiguously identified, a necessity
for performing the eigenvector overlaps.
operators. Double precision was used so that
degenerate pairs of eigenmodes could be unambiguously identified, a necessity
for performing the eigenvector overlaps.
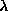 , the static vortex structure was found
using the relaxation procedure described in Section ii. This static
structure acquires nonzero out-of-plane spin components for
, the static vortex structure was found
using the relaxation procedure described in Section ii. This static
structure acquires nonzero out-of-plane spin components for
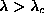 . Then, the eigenvalue problem [Eq. (2.14)] was
solved numerically for the eigenvectors and corresponding eigenvalues, for
systems with hundreds of sites. Because there are two variables per site, the
size of the matrix to diagonalize is
. Then, the eigenvalue problem [Eq. (2.14)] was
solved numerically for the eigenvectors and corresponding eigenvalues, for
systems with hundreds of sites. Because there are two variables per site, the
size of the matrix to diagonalize is 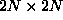 , where N is the number of
sites in the lattice. Calculations were performed for approximately circular
shaped systems, with the vortex centered in the system. For these finite
systems, there is a choice of either a free boundary condition or a fixed
boundary condition. For the free boundary condition, the lattice is cut off
along a circular boundary, and then the sites on the edge of the system simply
have a lower coordination number than those in the interior, and have a lower
effective stiffness as a result. For the fixed boundary condition, the set of
spins on the boundary of the system is coupled to an extra set of spins that
are outside the system, still on the same lattice, but held fixed in the
directions that the static in-plane vortex would give them. In this way, even
the spins at the edge of the system have the same coordination number as those
in the interior, however, they are coupled to spins that do not move that are
outside the system. Therefore, this fixed boundary condition, which is stiffer
than the free boundary condition, tends to give higher eigenfrequencies.
Additionally, the fixed boundary condition results in values for
, where N is the number of
sites in the lattice. Calculations were performed for approximately circular
shaped systems, with the vortex centered in the system. For these finite
systems, there is a choice of either a free boundary condition or a fixed
boundary condition. For the free boundary condition, the lattice is cut off
along a circular boundary, and then the sites on the edge of the system simply
have a lower coordination number than those in the interior, and have a lower
effective stiffness as a result. For the fixed boundary condition, the set of
spins on the boundary of the system is coupled to an extra set of spins that
are outside the system, still on the same lattice, but held fixed in the
directions that the static in-plane vortex would give them. In this way, even
the spins at the edge of the system have the same coordination number as those
in the interior, however, they are coupled to spins that do not move that are
outside the system. Therefore, this fixed boundary condition, which is stiffer
than the free boundary condition, tends to give higher eigenfrequencies.
Additionally, the fixed boundary condition results in values for 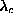 that converge faster to a limit with increasing system size, and for this
reason, most of the results reported here were produced with fixed boundary
conditions.
that converge faster to a limit with increasing system size, and for this
reason, most of the results reported here were produced with fixed boundary
conditions.