There are some finite size and boundary effects in these results that cannot be
avoided, but that do not invalidate the results. For example, the choice of
fixed boundary conditions eliminates the Goldstone mode related to global
rotation of the spins in the XY plane that is present for free boundary
conditions. However, the fixed boundary condition has the advantage that it
reduces the spin fluctuations at the boundary, whereas the free boundary
condition artificially enhances those boundary fluctuations. These are minor
differences. The effect of the finite sized system, for the most part, can be
understood to produce a finite frequency spacing between the modes, that
becomes smaller as the reciprocal system length. This causes the frequency
scale of the soft mode (a) at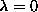 
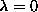, in Fig. 6, to go to zero
for the infinite sized system, which is partly an artifact of the calculation,
because this is the lowest mode for fixed boundary conditions. For the free
boundary conditions, this soft mode lies higher up in the spectrum. In a real
system of physical interest at some temperature above the Kosterlitz-Thouless
temperature, we could not consider an isolated vortex and its normal modes,
because entropic effects would always produce a length scale (i.e., correlation
length) at which the nearest neighboring vortex would be found. Thus, it may
not be necessary to consider the infinite sized system limit, because the
neighboring vortices will produce an effective finite length scale over which
we might think that the vortex is restricted.