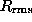To study the tendency of the vortex to concentrate a mode near its core,
we define the rms spread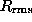 
of a wavefunction using the
total in-plane plus out-of-plane fluctuations as a weighting factor, as follows;
In a similar way, the rms spread of the system itself can be evaluated by
using a constant weighting factor. For the system with 180 sites that is
discussed in Figs. 7, 8, and 9, the rms spread of
the system is 5.355 lattice constants. The rms spreads of the lowest
frequency wavefunctions are shown in Fig. 11. There is a substantial
reduction in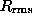 
for the soft mode as
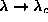, while for the other modes there tends to be
less drastic changes. Only mode (b1), which crosses the soft mode (a) slightly
above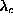 
, shows a similar sized change. Because the soft mode has
an rms spread much smaller than the rms spread of the system fo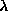r 
near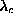 
, we interpret this to mean that the soft mode is a mode
localized on the vortex, while the other lowest modes are more extended over
the whole system. It is possible that there could be other modes higher up in
the spectrum which are also localized in this sense, but it could be difficult
to detect them because of the limited size of the systems that can be easily
solved numerically.
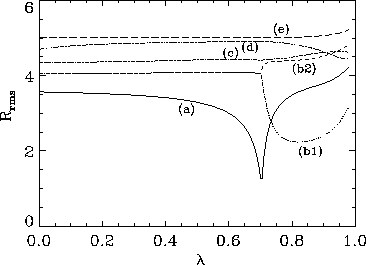
Figure 11:
The rms spreads of the 6 lowest frequency wavefunctions
for the square lattice system with 180 sites, versus anisotropy
parameter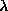 
. The letters refer to the modes shown in
Figs. 4--6. For the lattice itself, 
,
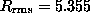while the radius of the system is about 8 lattice constants.
