


Next: Discussion and Conclusions
Up: NORMAL MODES OF VORTICES
Previous: RMS Mode Sizes
For comparison, we have also calculated the spectra for finite circular
systems on triangular and hexagonal lattices. The same methods as described
above for the square lattice were used, in which the primary physical
difference is the coordination number z=6 for the triangular lattice,
and z=3 for the hexagonal lattice. This leads to the different values
of 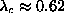 for the triangular lattice, and
for the triangular lattice, and 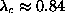 for the hexagonal lattice, as seen in the spectra shown in
Fig. 12. These results are completely consistent with the Ansatz
calculation for this mode. [23] There are substantial similarities in the
spectra for the different lattices, including the splitting of the degeneracies
for
for the hexagonal lattice, as seen in the spectra shown in
Fig. 12. These results are completely consistent with the Ansatz
calculation for this mode. [23] There are substantial similarities in the
spectra for the different lattices, including the splitting of the degeneracies
for 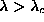 , the modes with downward cusps at
, the modes with downward cusps at 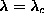 ,
and the one component of the lowest degenerate pair coming close to zero
frequency somewhat above
,
and the one component of the lowest degenerate pair coming close to zero
frequency somewhat above 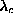 . On the other hand, the symmetries of the
lattices lead to small differences in the wavefunctions (not shown here).
. On the other hand, the symmetries of the
lattices lead to small differences in the wavefunctions (not shown here).
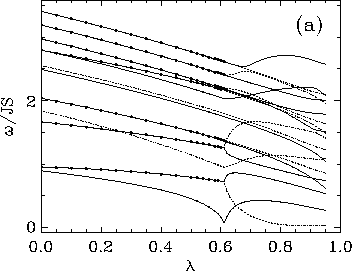
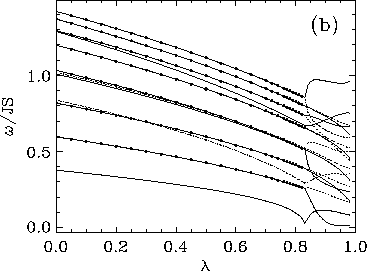
Figure 12:
Normal mode spectra (lowest 19 modes) of circular systems
containing a vortex at the center, with fixed boundary conditions, for
(a) triangular lattice with 174 sites; (b) hexagonal lattice with 192 sites.
While many features of these results also appear in Fig. 2,
the different values of 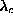 are notable.
are notable.
Gary M Wysin
Mon Sep 11 12:02:10 CDT 1995
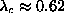 for the triangular lattice, and
for the triangular lattice, and 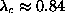 for the hexagonal lattice, as seen in the spectra shown in
Fig. 12. These results are completely consistent with the Ansatz
calculation for this mode. [23] There are substantial similarities in the
spectra for the different lattices, including the splitting of the degeneracies
for
for the hexagonal lattice, as seen in the spectra shown in
Fig. 12. These results are completely consistent with the Ansatz
calculation for this mode. [23] There are substantial similarities in the
spectra for the different lattices, including the splitting of the degeneracies
for 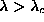 , the modes with downward cusps at
, the modes with downward cusps at 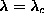 ,
and the one component of the lowest degenerate pair coming close to zero
frequency somewhat above
,
and the one component of the lowest degenerate pair coming close to zero
frequency somewhat above 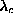 . On the other hand, the symmetries of the
lattices lead to small differences in the wavefunctions (not shown here).
. On the other hand, the symmetries of the
lattices lead to small differences in the wavefunctions (not shown here).


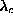 are notable.
are notable.