


Next: Normal Mode Wavefunctions
Up: RESULTS: SQUARE LATTICE
Previous: Size and Vortex
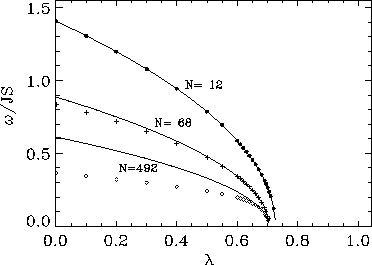
Figure 5:
Asymptotic least square fits (solid curves) of the frequency of
the soft mode (data points) for square lattice circular systems with
12, 68, and 492 spins, using the functional form
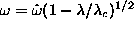 .
Only the data with
.
Only the data with 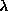 very close to
very close to 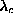 were
used to obtain the fitted curves. This functional form fits well over
the full range of
were
used to obtain the fitted curves. This functional form fits well over
the full range of 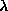 only for small systems (
only for small systems (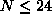 ).
).
For fixed boundary conditions, the soft mode for  has been
fit to the following functional form, as suggested through the simple Ansatz by
Wysin [23];
has been
fit to the following functional form, as suggested through the simple Ansatz by
Wysin [23];

where 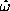 and
and 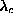 are the fitting parameters. Generally,
if all the data where
are the fitting parameters. Generally,
if all the data where 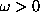 are used in the fit, this functional form
produces an accurate fit only for the smaller systems, up to about 24 spins.
More generally, we can use only a limited number of the data points nearest to
the zero frequency point, and apply this form there to estimate
are used in the fit, this functional form
produces an accurate fit only for the smaller systems, up to about 24 spins.
More generally, we can use only a limited number of the data points nearest to
the zero frequency point, and apply this form there to estimate 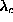 .
Some typical asymptotic fits are shown in Fig. 5, for systems with 12,
68, and 492 spins. The values of
.
Some typical asymptotic fits are shown in Fig. 5, for systems with 12,
68, and 492 spins. The values of 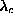 determined this way converge to
a limit near
determined this way converge to
a limit near 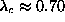 for the infinite sized system. The
frequency of the soft mode at
for the infinite sized system. The
frequency of the soft mode at 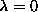 ,
, 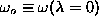 ,
gives an indication of the overall frequency scale for this mode, and is shown
in Fig. 6, versus system size (numbers not obtained from any
fitting). The result is compared with an asymptotic fit to the function,
,
gives an indication of the overall frequency scale for this mode, and is shown
in Fig. 6, versus system size (numbers not obtained from any
fitting). The result is compared with an asymptotic fit to the function,
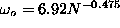 . This is close to a linear dependence on
inverse system length.
. This is close to a linear dependence on
inverse system length.
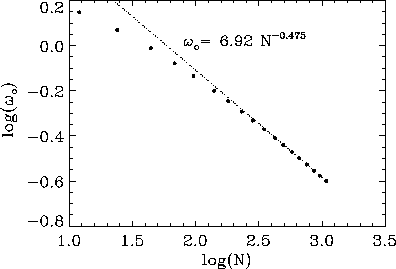
Figure 6:
Size dependence of the soft mode for square lattice
circular systems with N sites, using fixed boundary conditions.
The frequency 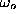 of the soft mode at
of the soft mode at 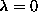 is shown on a log-log plot, and
compared with an asymptotic fit to the function,
is shown on a log-log plot, and
compared with an asymptotic fit to the function, 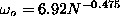 . This is close to a linear dependence on inverse
system diameter.
. This is close to a linear dependence on inverse
system diameter.



Next: Normal Mode Wavefunctions
Up: RESULTS: SQUARE LATTICE
Previous: Size and Vortex
Gary M Wysin
Mon Sep 11 12:02:10 CDT 1995

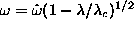 .
Only the data with
.
Only the data with 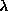 very close to
very close to 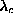 were
used to obtain the fitted curves. This functional form fits well over
the full range of
were
used to obtain the fitted curves. This functional form fits well over
the full range of 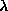 only for small systems (
only for small systems (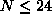 ).
).  has been
fit to the following functional form, as suggested through the simple Ansatz by
Wysin [
has been
fit to the following functional form, as suggested through the simple Ansatz by
Wysin [
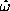 and
and 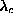 are the fitting parameters. Generally,
if all the data where
are the fitting parameters. Generally,
if all the data where 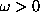 are used in the fit, this functional form
produces an accurate fit only for the smaller systems, up to about 24 spins.
More generally, we can use only a limited number of the data points nearest to
the zero frequency point, and apply this form there to estimate
are used in the fit, this functional form
produces an accurate fit only for the smaller systems, up to about 24 spins.
More generally, we can use only a limited number of the data points nearest to
the zero frequency point, and apply this form there to estimate 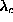 .
Some typical asymptotic fits are shown in Fig.
.
Some typical asymptotic fits are shown in Fig. 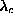 determined this way converge to
a limit near
determined this way converge to
a limit near 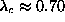 for the infinite sized system. The
frequency of the soft mode at
for the infinite sized system. The
frequency of the soft mode at 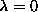 ,
, 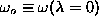 ,
gives an indication of the overall frequency scale for this mode, and is shown
in Fig.
,
gives an indication of the overall frequency scale for this mode, and is shown
in Fig. 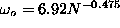 . This is close to a linear dependence on
inverse system length.
. This is close to a linear dependence on
inverse system length.

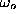 of the soft mode at
of the soft mode at 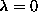 is shown on a log-log plot, and
compared with an asymptotic fit to the function,
is shown on a log-log plot, and
compared with an asymptotic fit to the function, 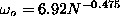 . This is close to a linear dependence on inverse
system diameter.
. This is close to a linear dependence on inverse
system diameter.