Research Description:
If you haven’t read my project overview yet, it might be a good idea to start there to get a general feel for both of the projects that I had the pleasure of working on this summer.
Project One: Token Bit Manager Chip Testing
One project that I got to work on this summer was testing token bit manager (TBM) chips. This project is headed by Dr. Andrew Ivanov and I worked closely with one of his post docs, Dr. Nikolas __. These chips are briefly explained in the project overview section of this website. The testing of these chips involved using a probe station in run electrical tests of several thousand TBM chips that will be used in the second upgrade stage of the large hadron collider (LHC) in Cern, Switzerland. TBM chip testing must be done extremely carefully as any dirt could permanently damage the chips and all the equipment is fragile and easy to break if managed improperly. The testing probe station must be aligned, calibrated and cleaned every day in order to ensure proper contact is made and the chips are able to be tested properly. The testing of these chips was set up in shifts where my partner Ramiro and I each did two to four hours of testing every day for the majority of the weeks of our REU program. This was a great experiment experience to compliment the mu2e project which is heavily theoretical.
Project Two: Mu2e: The Search for Muon to Electron Conversion
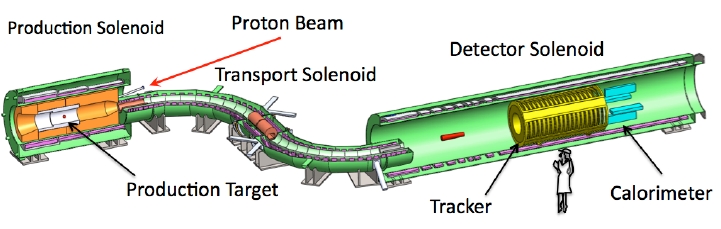
The mu2e experimental set-up. This image is broken up and explained alongside the experiment below.
Introduction and a Word on Mass and Energy:
The major project that I was able to work on this summer involved the experiment mu2e. Again, mu2e is explained briefly in the project overview section of this website and it may be worth reading that before continuing onwards. This experiment is seeking to detect a muon capturing on the nucleus of an atom and converting into an electron is through two detectors – one to measure momentum and the other to measure energy. It is important to note in particle physics energy is an important property that a particle has. Mass is able to me measured in energy and mass can be referred to as potential (stored) energy. This may seem absurd to think about at first, but you’ve certainly heard of E = mc2 which shows there is a direct relationship between energy and mass. The common unit for energy in particle physics is the electron volt (eV) and it is equivalent to 1.609 * 10-19 Joules (the SI unit of energy). A particle’s total energy is the sum of its mass energy (potential energy) and kinetic energy (which is based on how fast the particle is moving). A particle that is moving slowly will have a low amount of kinetic energy and a light particle will have a low amount of potential energy.
The Production of Pions and Why They Are Necessary:
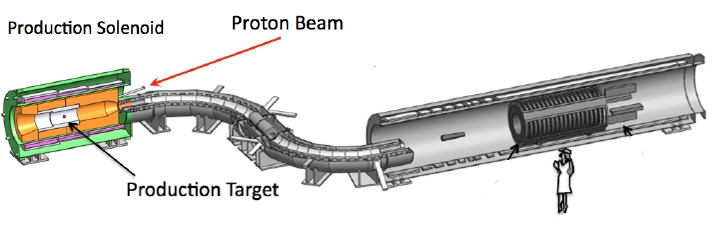
The production solenoid is left colored. You can see the proton beam coming in from the side that we want our pions/muons to go. This should give visualization to backscattering as only particles that are projected backwards are able to enter the rest of the system.
To begin this experiment, an 8 giga electron volt (GeV) pulse beam is fired at a tungsten target. The collision of the beam with tungsten produces many particles; one particular particle is a pion. Pions are particularly interesting because they can decay into muons. To get a general feel for particle interactions such as decay, there are a few important points to understand. Heavier particles are often more unstable than lighter particles and thus they want to convert or decay into a lighter, more stable particle. Pions are heavier than muons so it is favorable for them to decay into muons, but pions can also decay into other particles such as neutrinos and photons. There are often many interactions that a particle can go through, although some interactions are more likely than others. The probabilities of interactions that a particle can undergo can be calculated and experimentally tested based on advanced physics theories. Unstable particles also have a lifetime which is a prediction on the average length of time a particle lasts before it converts into a more stable one.
Back to the point – pions. Pions among other particles are produced by the proton beam hitting the production target and the pions that we are interested in are the back scattered ones, that is the ones that are produced with a backwards trajectory off the tungsten target rather than a trajectory that is in the same direction as the proton beam (see picture). The back-scattered pions move slower than other particles that are produced which means they have lower kinetic energy which is important and will be explained further later. The disadvantage of using and wanting these slower pions is there are far fewer back-scattered particles than non-back-scattered particles, but that is a necessary tradeoff. The next step after production is transport. All particles such as pions, muons, neutrinos and electrons now enter the transport solenoid. It should be noted that during the entire experiment, particles will be decaying and interacting at different points in the solenoids where it is possible. So pions are randomly but probabilistically decaying into muons during much of this experiment. Anyways, as all these particles enter the transport solenoid, they begin to be filtered. The transport solenoid is not straight and thus particles must bend their path in order to make it to the third and final solenoid, the detector solenoid.
The Transport Solenoid and the Power of Magnetic Fields:
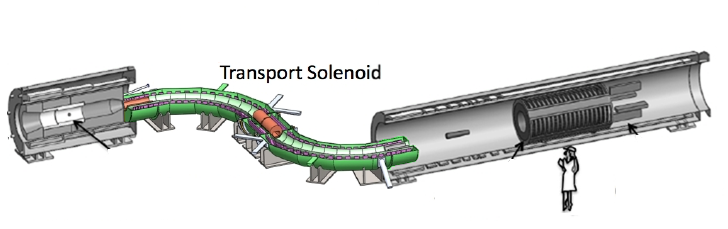
The transport solenoid is left colored. The shape of this solenoid is what allows particles to be able to be filtered out by magnetic fields if they don’t have specific charge and momentum. This solenoid also helps to slow down muons as they enter the detector solenoid.
One way to bend charged particles is to use a magnetic field. The direction a particle bends depends on the direction of the field and the charge of a particle; how sharply a particle bends depends on its momentum (mass and speed). Since we care about getting electrons which have negative charge from our muons, we only want the negatively charged muons to make it through the transport solenoid. A magnetic field is thus created using solenoids and it bends the negatively charged particles downward deeper into the system where the positive particles bend the other way out of the system and the uncharged particles keep flying straight through and out of the system (a particle must be charged to interact with a magnetic field). The geometry of the system no only filters out the positive and neutral particles, but it also filters negative particles that have too high or too low of momentum (relative to that of a muons desired in the experiment). Another side note is that not only does the transport solenoid use magnetic fields to control speed and direction of the charged particles involved, but the entirety of this experiment uses magnetic fields to do this.
The Detector Solenoid and the Ideal Scenario:
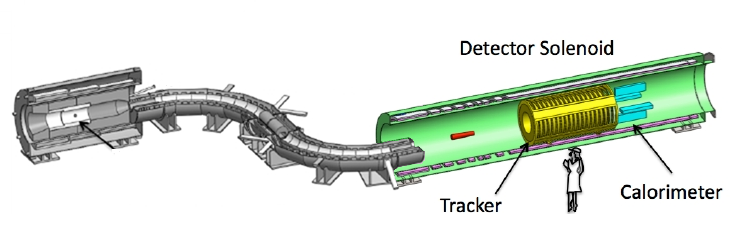
The detector solenoid is left colored. The red object in this detector is the aluminum target with which the muons will interact.
Finally we are in the detector solenoid where we ideally have mostly negatively charged pions and muons. The pions are not what we currently care about, but are important, especially to mine and my partner’s specific research goal this summer (further explanation below). Ideally what happens in the detector is that muons will capture on a target that is made out of aluminum. The aluminum isn’t altered in this interaction, but it is important that it is present because an atom is needed to drive this muon to electron conversion. During any interaction such as capture, total energy must be conserved (the amount of kinetic and potential energy is allowed to shift though, as long as total energy doesn't). If a muon is to really decay into only an electron with an aluminum nucleus spectating, the electron will have all of the muons energy. Muons are much more massive than electrons and thus have much more potential energy. This means that the electron must have much higher kinetic energy than the muon did to compensate for the potential energy loss. The muons that reach the aluminum target are moving very slowly thanks to back scattering and magnetic fields so we can assume the majority of its energy is its potential/mass energy which is about 105 mega electron volts (MeV). The potential energy of an electron is 0.511 MeV which means that an electron produced from muon decay should have mostly kinetic energy.
The Tracker and Calorimeter: How We Actually Detect Electrons:
Now the two detectors come into play. The first is the called the tracker and is used to measure momentum. Knowing the momentum serves two purposes, it allows scientists to determine that an electron came from the aluminum target and not somewhere else (all electrons of interest come from the aluminum target). The momentum also allows scientists to get an energy reading because a particles momentum is directly related to its kinetic energy and the potential energy of a particle doesn’t change – for an electron it is a stagnant 0.511 MeV. Unfortunately the tracker has a few disadvantages such that it cannot easily resolve what it is looking at, so although we can detect a particle’s momentum, scientists might not be sure what type of particle is actually being passed through. This is where the calorimeter comes into play. The calorimeter is less precise, but is able to work much faster which yields better time resolution and also a calorimeter is particularly good identifying that it is looking at an electron because calorimeter readings from electrons have distinct signatures. These two detectors complement each other and also allow two independent ways to get an energy reading which is provides further confidence and troubleshooting capabilities in the experiment.
Trouble in Paradise: The Background Noise of Radiative Muon Capture (RMC):
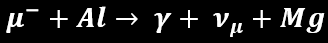
The above is an equation describing radiative muon capture. μ- is a negatively charged muon, γ is a photon and υμ is a muon neutrino. The photon is what can pose a problem to mu2e.
The goal of this experiment is to observe an electron with ~105 MeV of energy in the detector solenoid. Unfortunately it is not that easy as there are other particle processes other than muon capture that can lead to the presence of an electron with 105 MeV of energy in the detector. My personal project was to focus on radiative muon capture (RMC) whereas my partner, Ramiro Torres, was to focus on radiative pion capture (which is why it’s important to know that some pions do make into the detector solenoid. RMC is a process in which a muon is captured on a nucleus but instead of converting into only an electron it converts into a photon and a neutrino. The reason this is a big deal is that the photon can they in turn convert into an electron and positron (electron with a positive rather than a negative charge) pair. Going to back to energy conversation, when a muon converts into a photon and neutrino, its energy is distributed between the photon and neutrino. The percentage of energy that each particle gets from this conversion is random but probabilistic. There is a small chance that the photon can get the majority of the muons energy (where the neutrino would receive little energy) and then in turn when it converts into an electron positron pair, the electron gets the majority of that photons energy (where the positron gets very little energy). To put this into a perspective, RMC is not very likely to happen. When it does happen, the photon produced in RMC is not very likely to get the nearly all of the muon’s energy. On top of that, a photon is not likely to create an electron positron pair in the detector and if it does, it’s even less likely that the electron produced will get mostly all of the energy of the photon. However, this probability isn’t zero and must be considered. This kind of consideration should hopefully shed some light of the care and thought that is going into this experiment which seeks to reform the standard model.
Our Approach to RMC and My Personal Research Focus This Summer:
One approach to figure out if RMC is clouding the true mu2e signal is to measure the total amount of RMC electrons present, not just the RMC electrons that have high enough energy to be confused with the important 105 MeV electron mu2e hopes to find. This first one done using a hand calculation that took into consideration the geometry of the system and different probabilities in order to find out how many photons we can expect to enter and convert into an electron positron pair in the tracker. Photons can only produce an electron and positron pair in the presence of another material and since the inside of the tracker solenoid is a vacuum, the photon is not likely to convert in the tracker (if at all). This hand calculation is explained in our paper and the result of it is that we expect that 100s of millions of protons will convert in the tracker. We then moved on to computer simulation which showed us that around 100s of billions of photons convert in total between the tracker and the stopping target (we decided to take into account a bigger geometry).
The Result and Conclusion from Simulation:
My ultimate goal this summer was to show that radiative muon capture is a measurable and what the Mu2e collaboration can expect to see in terms from this process. The simulations were successful and you can view some of the results from that on my poster (link on the left). If the Mu2e collaboration chooses to measure the background then ignore it, they will not only account for this background, but also have tons of valuable data on radiative muon capture that can be used by another experiment or by Fermilab at a later time.
|

