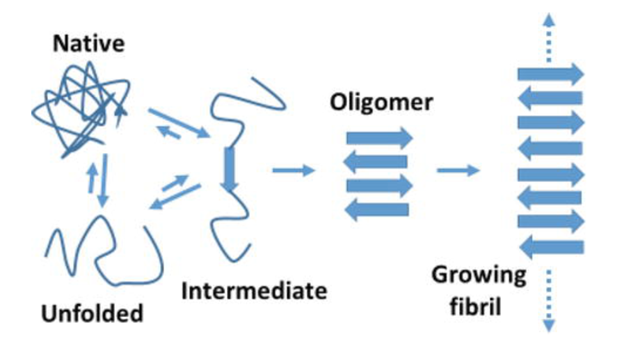
When proteins are misfolded, they can bind together to form long filaments known as fibrils. These aggregates are known to cause neurodegenerative diseases such as Alzheimer’s and Huntington’s. We are modeling aggregation rates of proteins because their kinetics may help us determine the mechanisms of fibril formation. Comparing our models to experimental data allows us to determine which modeling assumptions best reflect real biological systems.

Fig. 1. Proteins becoming fibrils. Source: https://www.intechopen.com/chapters/64516

In both of the models, each protein is represented as a blue or a red. When proteins line up correctly, they have a strong bond and we represent that protein as a blue. When the incoming protein does not line up with the previous one, it is represented as a red. This model gives us four possible configurations of two proteins: blue-blue, blue-red, red-blue, and red-red. Each has their own associated binding energy.

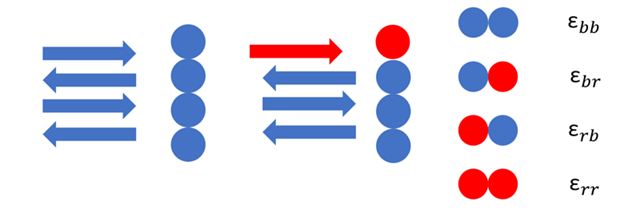Fig. 2. Proteins in a fibril represented as blue or red and their four possible configurations with binding energies.

The first way we are modeling rates is using a Monte Carlo simulation. This model simulates individual binding and unbinding events stochastically. It chooses between three possible events, each having its own rate. We model this using the Gillespie algorithm, which generates two random values between 0 and 1. The first value gives the time it takes for the next event to happen, and the second determines which event happens based on the ratio of the rates of possible events.

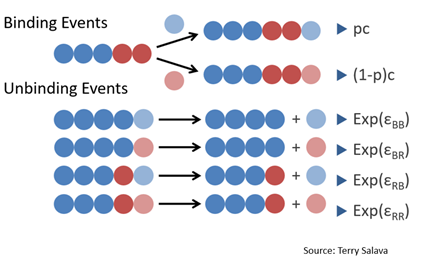Fig. 3. Each fibril can undergo three possible events: binding blue, binding red, or the last monomer popping off.

The other model is a partition function of the disordered cap. We assume quasi-equilibrium among all possible states of the cap and use Boltzmann weights to calculate the probability of each state. The partition function gives us the average behavior of the system by summing over all of the weighted states. While this model is valid at low concentrations, it falls apart at higher concentrations because equilibrium statistics no longer represent the actual rates.

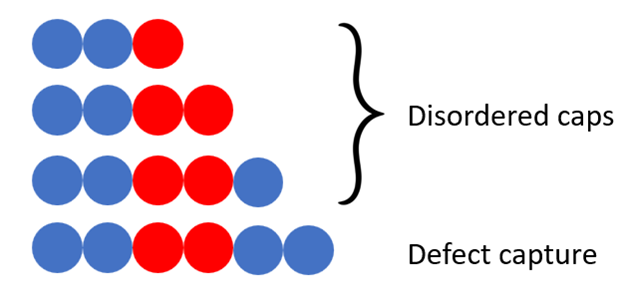Fig. 4. The disordered cap is wherever there is disordered binding not “captured” by two blues. Blue-blue unbinding is very unfavorable.

The results of both models are given here:

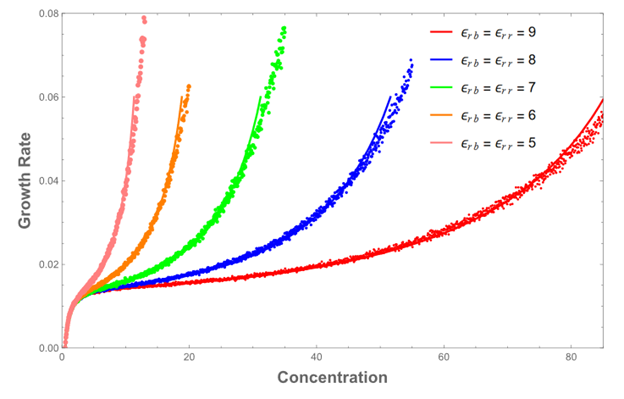Fig. 5. Solid line is partition function. Individual points are from running Monte Carlo model

They largely give the same results but differ when we expect them to (at high concentrations). Some effects of varying the binding energies are clearly reflected in the growth curves. The next step is to try to match the models to biological data.

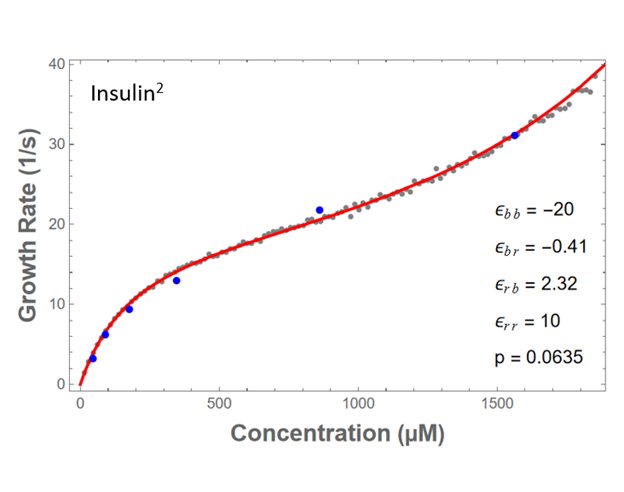Fig. 6. Red line is partition function. Grey points are simulation. Blue points are biological data from Buell et al., PRL (2010)

By fitting our models to biological data, we may be able to find relationships between the four binding energies.

Acknowledgments
Thank you to Dr. Jeremy Schmit and Terry Salava for your mentorship and guidance, and Dr. Loren Greenman, Dr. Bret Flanders, and Kim Coy for making this REU possible. This material is based upon work supported by the National Science Foundation under Grant No. 2244539. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Final Presentation