Neutrino physics is an exciting field of research in the 21st century, and the results from MicroBooNE have proven to be valuable to this field. The liquid argon time projection chamber that is used for the MicroBooNE detector allows for the reconstruction of tracks through the detector that result from ionizing particles traveling through it. Various properties such as kinetic energy, rate of energy loss, and the length of the tracks can also be retrieved to study the neutrino interactions that produced these particles. Protons are a particularly difficult particle to study because they lose energy very quickly and tend to produce much shorter tracks in the detector consequently. Furthermore, the vertex near the source of many tracks is often complex with many uncertainties due to the overlap of tracks and the high density of hits.

Due to the difficult nature of studying protons near the vertex, there is a concern that previous methods of measuring proton multiplicity may have some bias that focuses mainly upon tracks that are more easily identifiable as protons. To circumvent this potential bias, I first aim to select events with specific kinds of particles that are characteristic of the kinds of neutrino interactions that are likely to produce protons as well. Namely, these events are called charged current interactions, where a muon neutrino interacts with a nucleon via a charged (positive or negative) W boson. The most common instance of this produces one muon and one proton, but for the purposes of my project I am looking for events that produce at least one muon and one pion. Often, an interaction that produces a muon and a pion will also produce a proton because a positively charged pion and a proton are the decay products from a Δ++ resonance state.

Looking for these interactions allows for an unbiased look at both proton production and at the vertices of events because the tracks of the muon and pion travel far from the cluttered vertex region and can reliably be traced back to the vertex. Muons and pions create well-defined tracks through the MicroBooNE detector because they are both what is known as minimum ionizing particles (MIPs). These particles are considered minimum ionizing because they are relativistic particles with velocities close to the speed of light, which results in minimal energy loss per unit of distance as they travel through a medium. This means that they typically create very long tracks through the detector, which makes them easily distinguishable from other particles, such as protons. For this project, I use a Monte Carlo simulation that simulates neutrino interactions within the MicroBooNE detector to make a prediction of the proton multiplicity for charged current interactions with at least one pion, and then I use the same methods of analysis on MicroBooNE data from the real experiment in order to compare the prediction of our model to reality.

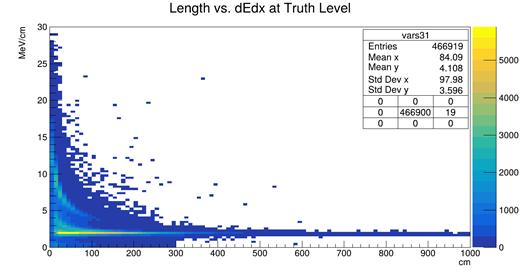
Fig. 1. Two-dimensional histogram from the simulation showing the distribution of tracks at various lengths in centimeters and rates of energy loss (dE/dx) in MeVs per centimeter.

In this histogram, we can identify two distinct structures that correspond to different classes of particles. First, in the upper left of this distribution, there appears to be a curve corresponding to a moderately high frequency of tracks that are generally highly ionizing and relatively short. Second, in the bottom of the graph there is a line running through about 2.1 MeV/cm with many tracks that tend to be comparatively long. This provides a clear picture of the differences between the properties of protons and MIPs, and we can consequently use these properties in order to isolate one or the other.

Given that I intend to study neutrino interactions with at least one muon and one pion, I apply a few cuts to the data to isolate these events. First, I require an event to have at least two tracks. Then, I identify the two longest tracks in that event, assuming that the longest tracks are the most likely to be minimum ionizing particles. Then, I apply cuts based upon dE/dx and length to ensure that the tracks are both MIPs.

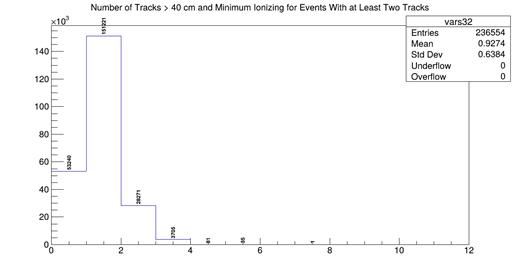
Fig. 2. Histogram showing the number of simulated tracks that make it past the dE/dx and length cuts for each event.

From this histogram, we can see that it is very common for an event with at least two tracks to nonetheless have less than two tracks that are expected to be from MIPs. This makes theoretical sense because muon-proton events should be much more common than muon-pion events. Thus, a condition has been added to require at least two tracks that both appear to be created by MIPs. Finally, we can predict the number of protons that are created in these events. Given that muon-pion events are likely to produce at least one proton, we assume that the remaining tracks for these events that have at least two tracks that meet the necessary conditions may all be protons that result from the argon nucleus breaking apart. First, I plot the total number of simulated tracks for events that have at least two tracks with the properties of minimum ionizing particles.

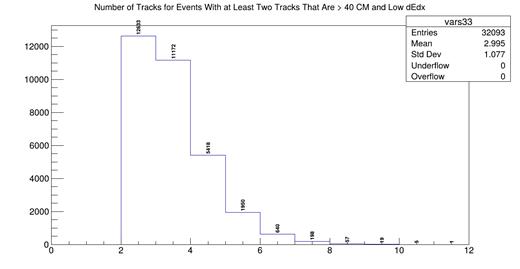
Fig. 3. Histogram showing the total number of simulated tracks for events that have at least two tracks with the properties of minimum ionizing particles.

Then, assuming two of these tracks are MIPs and that the remaining tracks are protons, I subtract two from this total.

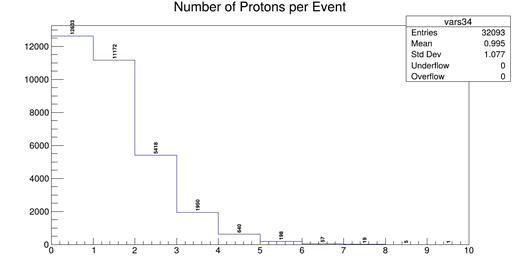
Fig. 4. Histogram showing the number of protons per selected event for the simulation.

Assuming that the remaining tracks are protons, the resulting distribution is a prediction of the number of protons produced per charged current interaction with at least one muon and one pion. Now, I can apply the same methods of analysis to the MicroBooNE data to make a measurement.

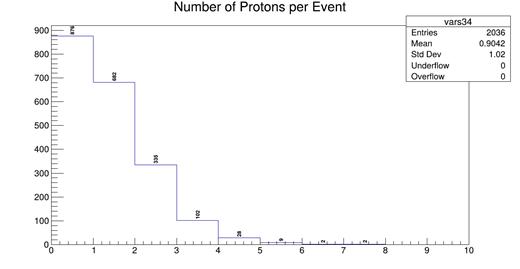
Fig. 5. Histogram showing the number of protons per selected event for the open data.

The distributions are qualitatively similar but show some disagreement. The zero bin is higher for the open dataset than in the simulation, and the simulation shows higher multiplicity in most other bins. Furthermore, the mean number of protons produced for each event is significantly lower for the MicroBooNE data (0.90) compared to the Monte Carlo simulation (1.00). It is also worth noting that the standard deviations are different, with the MicroBooNE data's standard deviation being 1.02 and the Monte Carlo simulation having a standard deviation of 1.08. There are far more entries in the simulation as compared to the MicroBooNE data. This is because the simulation has over one million events, whereas the open dataset for MicroBooNE has only about 170 thousand events. In addition, many of the events in the open data are caused by cosmic rays instead of neutrino interactions, and thus they do not pass the event selection cuts. A chi-squared test between the simulation and the open data for the first eight bins shows relatively poor agreement with a value of about 19.77 with 7 degrees of freedom. This corresponds to a p-value of 0.006, which means that with 99.4% confidence I can reject the hypothesis that the Monte Carlo simulation accurately predicts the proton multiplicity of νμ-Ar charged current interactions with at least one pion. One possible explanation of this is that the simulation is less likely to predict that a proton might be immediately re-absorbed by the Argon nucleus, which could be what results in the open dataset having a greater number of events where there are zero tracks from protons. In fact, this finding is consistent with other observations.

Acknowledgements

I would like to acknowledge Dr. Tim Bolton, Kim Coy, Dr. Loren Greenman, Dr. Bret Flanders, Norman Martinez Figueroa, and Adil Hussain, who were all essential to my work here. This material is based upon work supported by the National Science Foundation under Grant No. 2244539. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. I also acknowledge the work of the MicroBooNE collaboration for giving me access to the data and the Monte Carlo simulation.

Final Presentation