The natural precipitation of calcite (calcium carbonate) is responsible for removing ~ 1 gigaton of carbon dioxide from the atmosphere every year. We suggest that the presence of water in mineral-rich soils allows for solutions highly super-saturated (high-S) with calcite's growth units to form. High-S solutions are also present in manufactured carbon-capture processes. These high-S solutions exhibit rapid calcite precipitation, making them of key interest. The relationship between fast calcite crystal growth rates and high-S solutions has not yet been well-characterized, and understanding this relationship serves as the goal of my project.

Fig. 1. Naturally formed calcium-carbonate, seen as the Cliffs of Dover.

A key component of our experiment was inducing locally high-S solutions via the presence of two dissimilar metals, which formed a galvanic couple. These galvanic couples induced a positive pH shift at one of the electrodes, increasing the solution's supersaturation at that electrode. We used the gold surface of a quartz crystal microbalance (QCM) as one of the electrodes in our galvanic couple, and that same gold surface serves as the site of our calcite precipitation. A QCM is capable of measuring small changes in mass underwater, and as such this tool provided accurate mass overtime curves for small calcite crystals in the presence of high-S solutions. With a numerical fitting method, we were able to extract calcite crystal growth rates from the data provided by our QCM. This process was performed with a variety of galvanic couples, and the effects of each couple were analyzed in detail.

The process by which a galvanic couple locally raised a solution's supersaturation at one electrode relied on an important condition. It was assumed that the solution containing said couple was in a state of atmospheric equilibrium. That is to say, the exchange of carbon dioxide between the solution and the atmosphere had reached a point of stability. Under this condition, the concentration of carbonate (one of calcite's two building blocks) in the solution, scaled exponentially with pH. Under the same condition, an increase in the hydroxide concentration of a solution lead to an increase in the solution's pH. Refer to Fig. 2 for a quick visual explanation of the process.

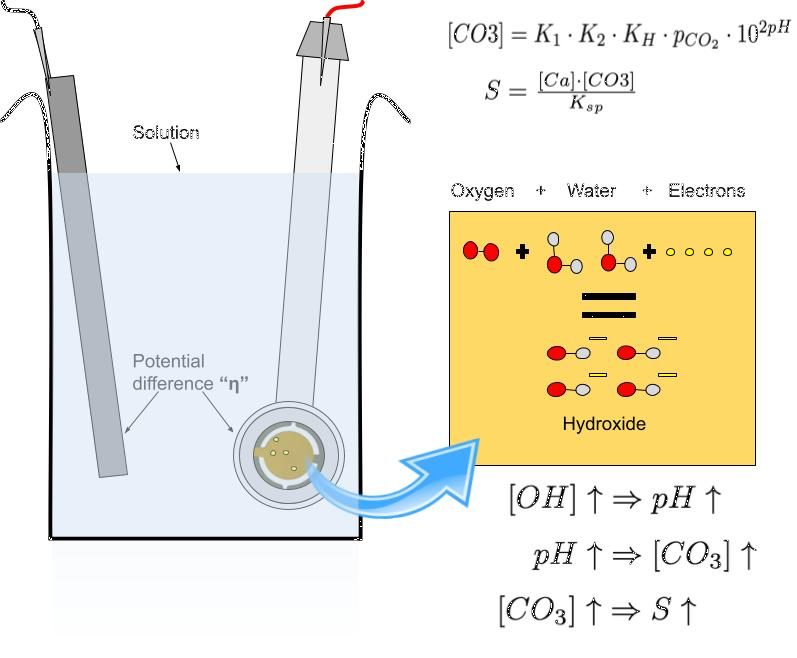
Fig. 2 One electrode of a galvanic couple lent electrons to the solution, forming hydroxide in the process. This in turn raised the pH, ultimately increasing the supersaturation of the solution.

There were several difficulties in quantifying the (fast) growth rates of calcite crystals. Many of the difficulties in measurement were accounted for by the QCM, however some remained unaddressed. One such difficulty was the variability of a given calcite crystal's growth rate during an experiment due to diffusion-limitations. As our crystals increased in size, so too did their active growth areas. At a critical size, our crystals began to consume growth units faster than such units could be supplied by the surrounding solution. At this point, the growth rates of our crystals deflected from their otherwise constant values during the early, reaction-limited phases of our experiments. By utilizing a stir plate, we suppressed the effects of this limitation to the best of our ability by constantly reintroducing growth units to our crystal.

To better combat the effects of diffusion limitation and increase the lengths of our experiments, we utilized a "seeding" method. Note that our calcite crystals were actually clusters of ~2,000 small individual crystal nuclei called seeds. These clusters of seeds were integral to our method. Such clusters were capable of having a measurable overall mass, all the while without reaching a point of diffusion limitation. The drawback of this method was that the total seed count introduced a new variable, and a precise measurement of this count was necessary. As such, a high-resolution camera was used to image our seeds. With Python, these seeds could be easily counted. With multiple images, it was possible to verify whether or not the number of seeds remained constant across the experiment.

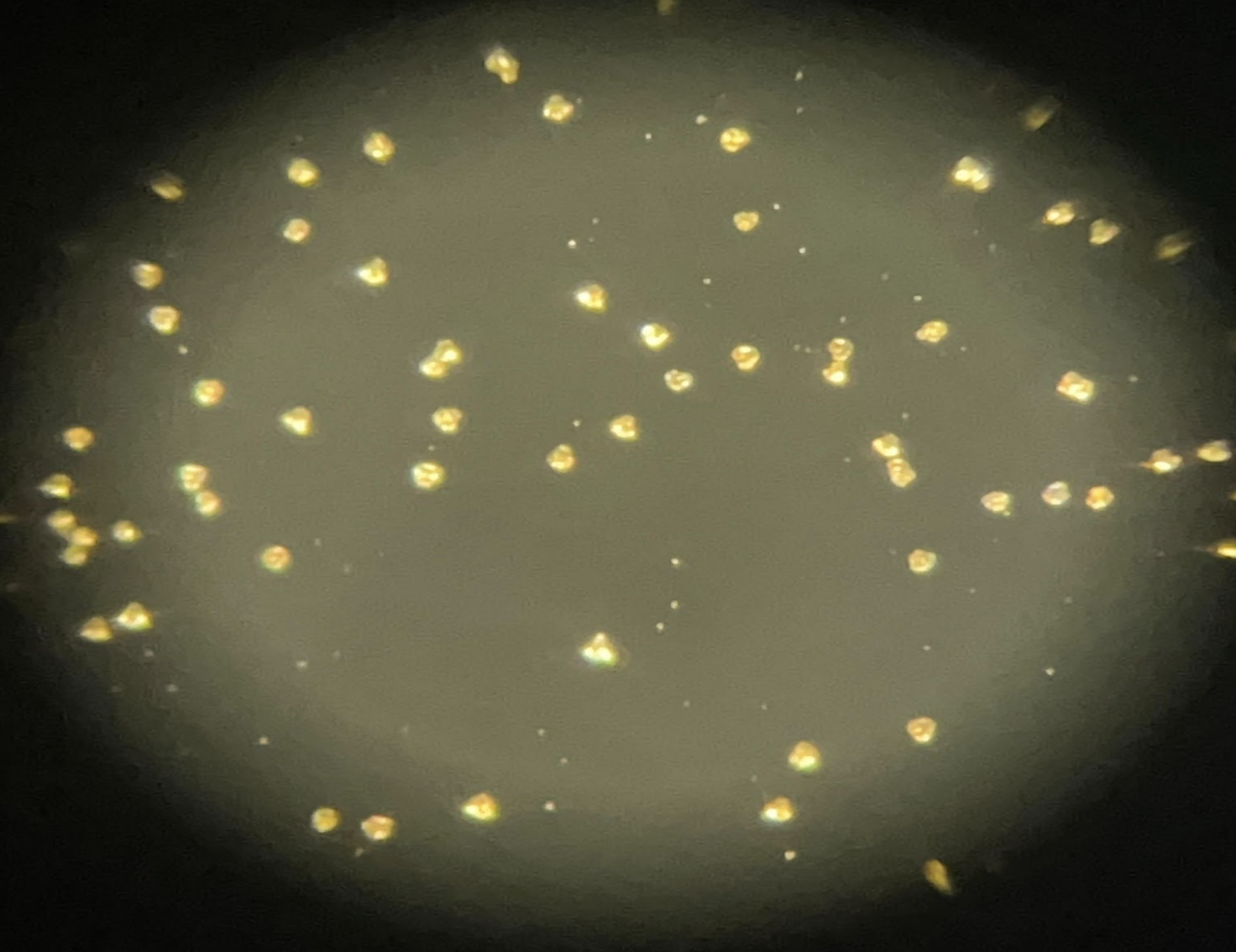
Fig. 3 A zoomed-in image of our calcite seed cluster.

To produce this array of seeds, we used a standard seeding routine, as shown in Fig. 4. A trio of electrodes allowed for a local pH shift to take place at our gold QCM electrode, the 'working electrode.' The plate was simultaneously imaged via a microscope, and the QCM was removed from the growth solution after a given amount of initial calcite mass had formed on the plate. This process circumvented the long wait time required for spontaneous calcite nucleation.

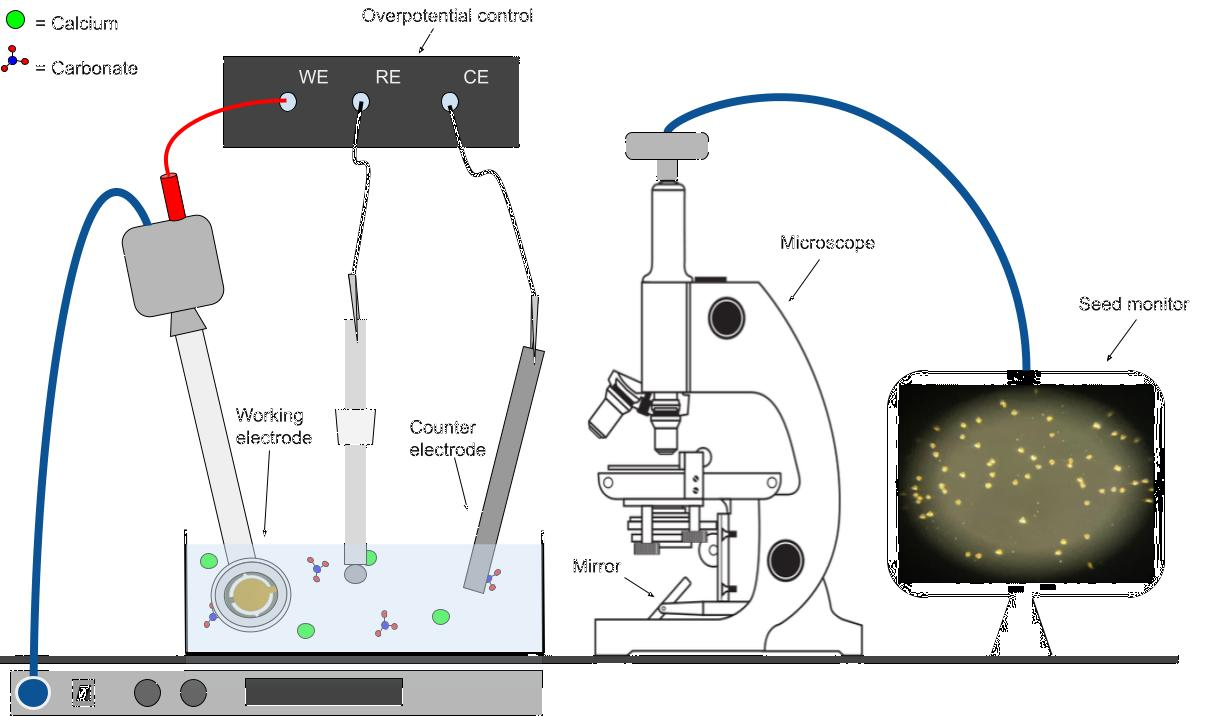
Fig. 4 A schematic of calcite seeding. The QCM actively provided a 'frequency offset.' This offset corresponded to an initial mass. When the offset reached -5 hertz, the QCM was pulled from the solution. This process allowed for an accurate characterization of the initial calcite seed count and initial calcite mass.

After seeding our plates, we allowed our QCMs and the calcite seeds upon their surfaces to sit in a 'holding' solution for ~10 minutes. During this time, a new 'growth' solution was prepared, in which the bulk of our calcite crystals would grow. These solutions possessed a known total concentration of calcium ions, as well as a known concentration of chloride and sodium ions used in controlling the pH of our solution. Once the QCMs were placed in the growth solution, a second metal was introduced to form a galvanic couple. We allowed for the repeated connection and disconnection of our galvanic couples during the experiment. Additionally, our solution was stirred during the periods of disconnect. With our setup, we were able to extract important time plots for our calcite masses, solution pHs, galvanic currents, and open circuit potentials (OCPs). After a significant amount of mass had formed, we removed our QCMs from the solution and imaged the calcite crystals a second time. Refer to Fig. 5 for a stripped-down schematic of this growth phase process.

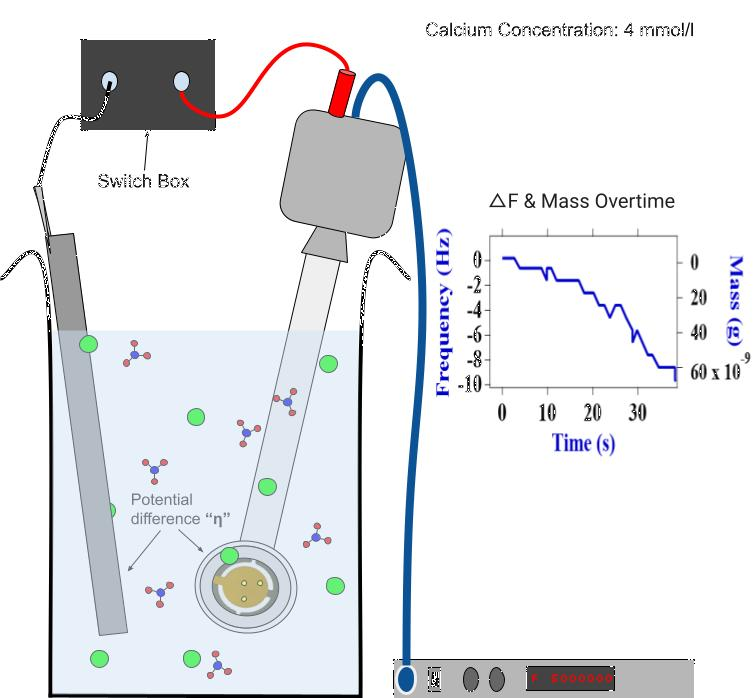
Fig. 5 Our QCM assumed the role of an electrode in a galvanic couple. The solution in which it sat contained a given concentration of calcium, and the increase of local pH allowed for a rapidly increasing mass overtime curve to form.

With our data, we were able to extract calcite crystal growth rates using a numerical fitting method. A theoretical mass overtime function was derived, as shown in Fig. 6. Note that the initial masses of our calcite crystals, along with initial calcite seed counts, were the only two parameters in need of defining. Our initial masses were recorded via the QCM during our seeding phase and had little variability. Quantifying the seed counts N presented more difficulty. For our fit to work as expected, the time independence of our N values was critical. By imaging our calcite crystals both before and after the growth phase of our experiment, we were able to assess the degree to which new seeds formed during the growth phase. If relatively few new seeds formed, our data was analyzable and Python was able to provide us with an estimate of N. With knowledge of our two parameters, we were able to fit our data in a realistic timeframe, before diffusion-limitation set in.

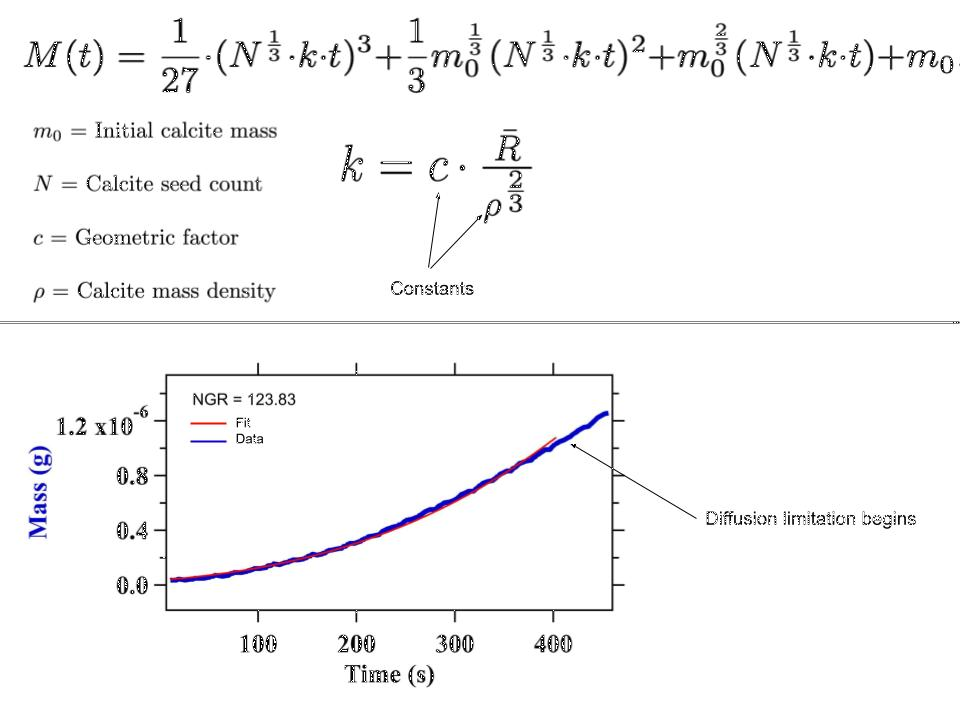
Fig. 6 A theoretical fitting function for the mass over time of a calcite seed cluster. Note that as time goes on, the fit and the data diverge. This is due to the diffusion-limitations described above.

As a result of the methods above, the quantification of fast calcite growth rates in high-S was made possible with relatively little equipment. S could be extracted from the data via pH, and our fitting method allowed for an assessment of our growth rates. Note that a variety of galvanic couples were used. Different galvanic couples exhibited different OCPs, and the extent to which our solution supersaturations were raised near our QCM relied upon these OCPs. For couples with larger OCPs, the supersaturation shifts were larger. We averaged the growth rates of calcite crystals exposed to various galvanic couples across multiple trials and plotted these rates against the galvanic couples' OCPs. Fig. 7 shows a collection of data sets and their corresponding fits belonging to a gold-titanium galvanic couple. By averaging the growth rates and the OCPs of these experiments, we produced a point on a much larger plot displaying the relationship between calcite crystal growth rates and galvanic couple OCPs. The relationship between these two measurements is still being assessed.

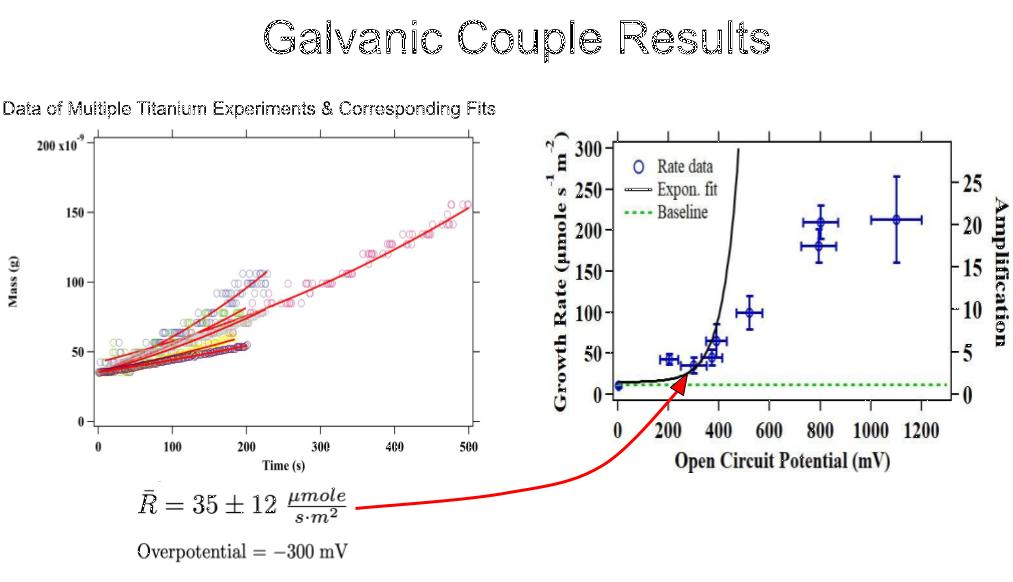
Fig. 7 A plot showing the many datasets of calcite crystals' masses over time when titanium-gold galvanic couples were present (left). A master plot showing the averaged growth rate of calcite crystals vs. the OCPs present during crystal growth (right).

In conclusion, we see that the unique methods present in our lab allowed for the accurate quantification of calcite crystal growth rates in high-S solutions. Additionally, we observed a relationship between galvanic couple OCPs and calcite crystal growth rates. Going forward, we hope to shift our source of calcium away from a chemically prepared powder and towards a natural source, such as the untilled soil of Manhattan Kansas's Konza Prairie.

References
[1] Flanders, B. QCM-Based Growth Rates from Seeded Substrates.

[2] Flanders, B. Scaling of CaCO3 Electro-Precipitation Rates with Overpotential.

[3] Flanders, B. Species Concentrations in Supersaturated Ca++/CO3−− Solutions.

Acknowledgements
I would like to thank the NSF for funding my participation in this program. In addition, I would like to thank Prof. Bret Flanders and Cade Ifland for guiding me throughout my research. I would also like Kim Coy, Prof. Bret Flanders, and Prof. Loren Greenman for organizing K-State's 2024 physics REU. Finally, I would like to extend my thanks to the other students participating in this year's REU program. This material is based upon work supported by the National Science Foundation under Grant No. 2244539. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Final Presentation