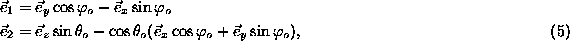
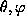 from
those in the vortex solution,
from
those in the vortex solution, 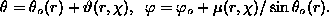 In local rotated coordinate
frames,
In local rotated coordinate
frames, 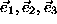 , where the axis
, where the axis 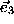 coincides with the
coincides with the 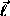 -vector's direction in the
unperturbed vortex, and
-vector's direction in the
unperturbed vortex, and
the variables 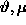 are the projections
of the
are the projections
of the 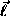 -vector on the local axes
-vector on the local axes 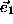 and
and 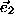 :
: 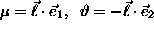 .
.
It is easy to get the coupled set of two partial differential
equations for 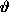 and
and 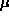 :
:
where
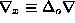 , and the ``potentials'' are:\
, and the ``potentials'' are:\
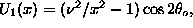
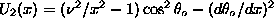 .
Using the ansatz like that in [8],
.
Using the ansatz like that in [8],
where 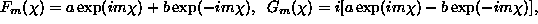 and
a,b are arbitrary constants, one obtains a coupled set of
ODEs for
and
a,b are arbitrary constants, one obtains a coupled set of
ODEs for 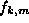 and
and 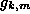 .
Here
.
Here 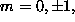 ...; k and m are the full set of
quantum numbers denoting the eigenvalues
...; k and m are the full set of
quantum numbers denoting the eigenvalues 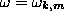 The presence of the combination of exponentials
The presence of the combination of exponentials 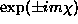 with arbitrary coefficients is due to the degeneracy of
the modes with m=+|m| and m=-|m|.
One can see that the coupling of
with arbitrary coefficients is due to the degeneracy of
the modes with m=+|m| and m=-|m|.
One can see that the coupling of 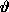 and
and 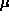 in Eq.
(6) comes from the term with
in Eq.
(6) comes from the term with 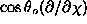 only. This means that (i) the
coupling vanishes exponentially at
only. This means that (i) the
coupling vanishes exponentially at 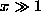 (
(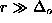 );
(ii) there is no coupling for m=0 modes, in contrast to
the FM case [8],[12].
);
(ii) there is no coupling for m=0 modes, in contrast to
the FM case [8],[12].