Mathematization:
Students’ Understanding of Taylor Series in Electricity and Magnetism
by: Dylan E. McKnight
supervisor: Eleanor C. Sayre, Assistant Professor of Physics
Kansas State
University Physics Department REU Program Sayre Lab Homepage



Welcome to my webpage.
Project
Overview: This
project is a small part of a much larger project called Mathematization.
Mathematization seeks to understand how students convert Physics problems into
Mathematics problems at the upper division. My project specifically pertains to
how students understand the Taylor Series in a Physics context. Through this we
hope to learn how to effectively teach complicated concepts such as the Taylor
Series. The data we are looking at is video recordings taken over a semester at
Kansas State University. We observe student behavior through the videos, and
then analyze it using theoretical frameworks. This has two outcomes:
1.
It helps us
understand how Physics Students at the upper division draw Mathematics from a
physical system.
2.
It begins to shed
light on how instruction style affects students understanding of complicated
topics, like the Taylor Series.
Research
Description: This project is a video based microanalysis of
intra-group conversation in upper division Electricity and Magnetism I. By
employing progressive refinement of hypotheses we generate emergent claims. We
then test those claims using the Resource Framework with the video data as
evidence.
Let
us clarify some jargon. A microanalysis
means that we are focused on small timescales. A small timescale would roughly
be between 1-20 minutes. Intra-group
conversation means that we are interested in the conversations within the
groups of students, not the conversations between independent groups of
students. Progressive refinement of
hypotheses1 is a method by which you form a hypothesis, and then
test it against data. If the hypothesis does not fit the data, you modify the
hypothesis, and repeat the process. An emergent
claim is one that is generated by the analysis of data, not prior to the
analysis of the data.
The
Resources Framework is the tool we
use to analyze our video data. A resource
is a “chunk of knowledge that students bring to bear on a situation.”2 For example, think of Intensity. The closer you are to
something, the more intense it is. Someone could take that in conjunction with
Temperature to form the thought the closer
I am to something, the hotter I feel.
We
can visualize this with a tool called a resource
graph.3
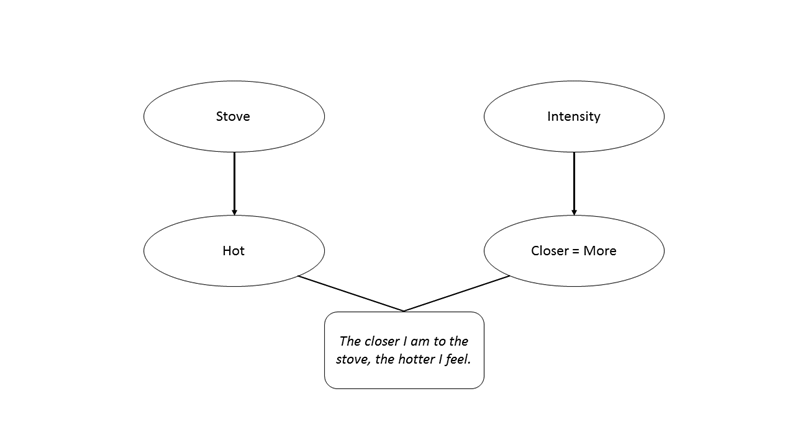
The
aspect of the project that went through the largest change was the Resource
Graph I used to explain the students’ thought processes. Early in the project,
I envisioned the Taylor Series as a rather straightforward concept.
The Taylor Series: 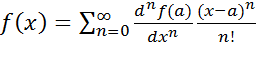
Let
us think about the aspects of the Taylor Series. The base operations are:
1.
Addition
(Summation)
2.
Multiplication
(Factorials, Exponents)
3.
Differentiation
However,
there is also an aspect that sets a Taylor Series in Mathematics apart from a
Taylor Series in Physics; Physical Intuition. Rather than being told what the
expansion point, a, is, as in
Mathematics, students in Physics have to examine the physical system, and
determine a from it.
Arranging
all of this into a Resource Graph would yield this:
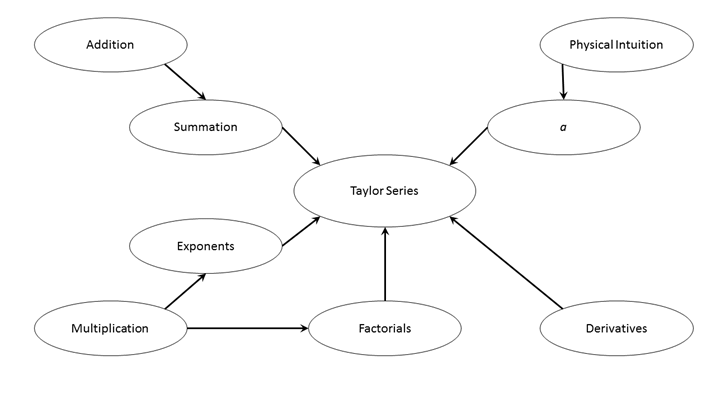
If
you think it is messy and confusing, you would be right, which is a primary
reason it was scrapped. The other, far more important, reason it was tossed at
the wayside was that it did not fit the data that well.
This
was surprising. The instructor had made a comment during class after a quiz
about Taylor Series; that she preferred to separate the Taylor Series into two
components; algebra and derivatives. If I had put some thought into instructor
framing, this would have been obvious to me from the start. Framing is how a piece of information is
presented; here it is being presented as a checklist.
Entertaining
this idea, I generated a new Resource Graph:
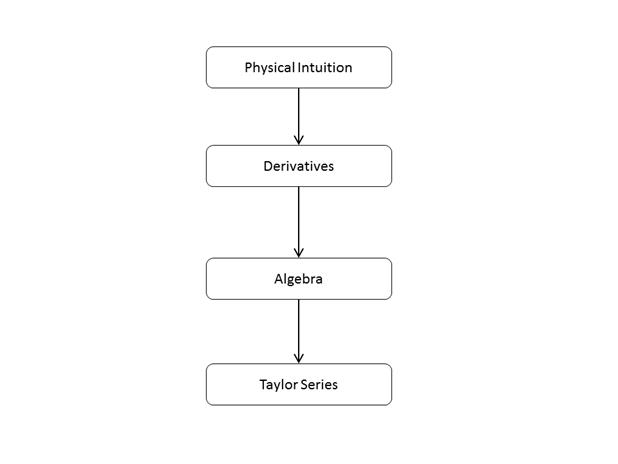
To
explain this resource graph, we require one more tool in the PER toolbox; the
idea of primitives and concepts.
A
primitive is a resource whose
internal structure is not explorable by the student.4
A
concept is a resource whose internal
structure is explorable by the student.4
The
idea behind this resource graph was to examine how students perform Taylor Series
in the checklist manor, as was framed by the instructor. Rather than individual
primitives, students were activating concepts one by one, and combining them at
the end to produce a Taylor Series. This is a fairly common way of teaching
Taylor Series in a Mathematics or Physics context.
The
problem with this resource graph is that it, like the previous one, disregards
the students’ thought processes. It oversimplifies the operation, and does not
allow individual nuance into the thought process.
Furthermore,
there was not data to test this hypothesis. In the data, students spent more
time deciding what to pick for a than
performing the mechanics of the Taylor Series. I was straying from my original
idea. I decided to focus on strictly the physical intuition concept, since that
was what the students spent the most time discussing.
I
abandoned the idea of primitives and concepts and returned strictly to
resources. After discussion with Dr. Sayre, we came to the idea of a
contradiction of logic.
Maybe students were having trouble
justifying how one value approaches 0 as another value approaches infinity.
We
took the idea and ran with it.
In
the data, we were observing students solve the problem: Find the Multipole Expansion of the potential of any localized charge
distribution, and express the answer in terms of 1/r.
The
problem is illustrated here:
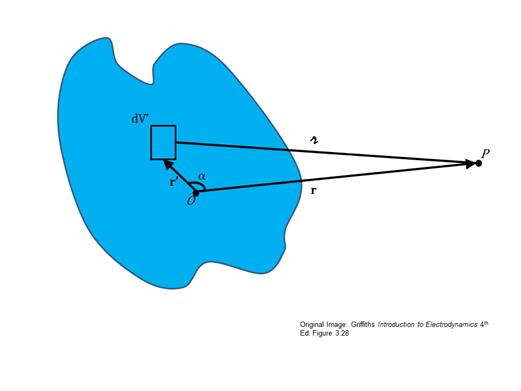
The
instructor set the problem up to the point where the students had the
expression: ![]()
Students
were required to determine the expansion point, a, in the Taylor Series Expansion:
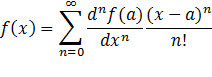
In
this task students are supposed to differentiate between an arbitrary expansion
point of a function (Mathematics), and a number with physical meaning.
(Physics)
The
main observations in the data were:
1.
This
differentiation between Mathematics and Physics is exceedingly difficult for
the students.
None of the students are able to give correct
reasoning for why a = 0.
2.
Students’ choice
of a depends highly on instructor
framing.
The instructor made a comment prior to this task: “It
is generally true that a = 0.”
Possibly because of this, some students were able to
give the correct a = 0 answer, but
not the correct reasoning.
One student’s reasoning for why a = 0 was “because we never choose anything else.”
3.
Students’ choice
of a also depends on prior experience
with Taylor Series. (The students had a quiz of Taylor Series the class before
Multipole Expansion, it was a Mathematics problem, and they were told what to
use for a.)
Two students had an exchange while reasoning about
what a should be (All names are pseudonyms
to protect confidentiality):
◦
Ed: a
was 0 here [Taylor Series quiz].
◦
Jim: This
[Multipole Expansion] is different but I don’t even understand what a
is.
◦
Ed: I don’t
particularly understand why a was 0 is that one [Taylor Series quiz]
either.
The students realize that there is something that
determines a, but they cannot
determine what that is.
Combining
all these observations, we generated to final resource graph:
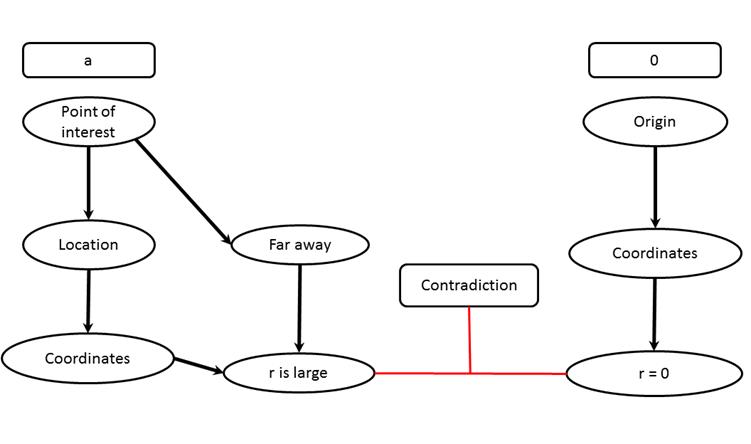
Think
of the graph like two columns, an a
column, and a 0 column. The resources in each column activate in a way such
that they converge at the bottom in a contradiction.
Final Presentation:
Click the link to view my Final Presentation. (.pdf format here)
Final Poster: Click the link to view my Final Poster. (.pdf format here)
About Me: I attend university at Saginaw Valley State University. I began there in August of 2012, and am expecting to graduate in May 2017. I am a double major in Physics and Mathematics.
I first became interested in Physics proper in high school. I took Physics as a junior and, like Mathematics, it was something that flowed naturally from my mind through my hands to the paper. Up until that point I had aspirations of an engineering or music career. However, from that point on, my mind became solely focused on Physics. I entered university declared as a Physics major. That is, until I took Calculus II as freshmen, and fell in love all over again. I declared my double major in Physics and Mathematics, and have never deviated.
My interests in Physics however, have. I began university as the Higgs Boson was becoming the big thing in Physics. I was determined to become a particle physicist, as were many green undergraduates at the time. I do not quite remember what caused the obsession to falter. It could have been that there were no particle physicists in SVSU’s Physics department. Regardless, I discovered Solid State Physics, and loved it. I conducted my senior research on the electric properties of solids, which we were going to measure via a Colpitts Oscillator. During this time, my interest in Physics Education began. My first real exposure to Physics Education Research was this REU, and it was enlightening. Beyond this REU, and my other research forays, I have entertained the ideas of Optics, Chemistry, Materials Science, and Electrical and Computer Engineering.
I have been a tutor at SVSU’s Center for Academic Achievement since August 2013. I tutor Physics, Mathematics, and Statistics. I am currently president of the Math Club at SVSU, formerly vice-president. I was formerly vice-president of Physics Club at SVSU, and am currently just a member.
The REU program has helped me grow in the following ways:
1. I learned everything I know about Physics Education Research (Resources, ACER, Responsive Teaching, Inter-Rater Reliability) during this REU.
2. I developed healthier research habits than I previously had (time management, self-guidance).
3. I met many great people.
4. I learned tons of interesting Physics (and Ethics) through the lectures.
5. I met people I would be interested in working with for graduate school that I would not have considered prior.
This program is funded by the National Science Foundation through grant number PHYS-1461251. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Mathematization is funded by the National Science Foundation through grant number 1430967. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

References:
1. R. Engle, F. Conant, and J. Greeno, 2007 Progressive Refinement of Hypotheses in Video-Supported Research
2. K. Black and M. Wittmann, 2009 Procedural Resource Creation in Intermediate Mechanics
3. E. Sayre, M. Wittmann, 2008, Plasticity of intermediate mechanics students’ coordinate system choice
4.
E. Sayre, M. Wittmann, J. Donovan, 2007, Resource Plasticity:
Detailing a Common Chain of Reasoning with Damped Harmonic Motion