Project Overview
Standard Big Bang nucleosynthesis (BBN) is used
to model the production of light elements D,
3He,
4He,
and
7Li during the first 20 minutes of
the development of the universe. With the baryon density determined
by cosmic microwave background (CMB) observations, standard BBN
predicts abundances of D,
3He,
and
4He that are in good accord with
the observed abundances, however, there is a large discrepancy for
7Li.
The observed
7Li
abundance appears to be depleted by a factor of about 3 when
compared to the prediction of standard BBN in conjunction with CMB
data. For recent reviews see
Jedamzik & Pospelov
(2009), Spite &
Spite (2010),
Steigman (2010),
Fields (2011),
Frebel & Norris (2011),
Spite et al. (2012),
and Coc et al. (2014).
7Li is a very fragile isotope that is destroyed at temperatures above 2.5×106 K. In stars that are too hot, convection within the star occurs close to the surface and leads to a mixing of the atmosphere and the hotter, deeper layers of the star, and destruction of 7Li. This has led to an emphasis on accurate stellar temperature measurements when determining A(Li). Ultimately, stellar 7Li is thought to be preserved and provides the best representation of the primordial abundance in warm, metal-poor dwarf, or turnoff, stars (Spite et al. 2012). A(Li) determined from these stars is lower than expected. While some have argued for higher observed primordial 7Li abundances (see e.g., Melendez & Ramırez 2004; Melendez et al. 2010; Howk et al. 2012), consistent with that expected from the CMB anisotropy data determination of the baryon density, here we focus on the more popular belief that standard BBN has a 7Li problem and try to more carefully quantify this discrepancy than has previously been done.
We construct the error distribution of 7Li abundance measurements for 44 observations (with error bars) used by Spite et al. (2012) that give A(Li) = 2.17±0.072 (median and 1σ symmetrized error). This error distribution is some- what non-Gaussian, with larger probability in the tails than is predicted by a Gaussian distribution. The 95.4% confidence limits are 3.0σ in terms of the quoted errors. It is reasonably well described by a widened n = 6 Student’s t distribution. Assuming Gaussianity, the observed A(Li) is 6.5σ away from that expected from standard Big Bang nucleosynthesis given the P lanck observations (Coc et al. 2014). Accounting for the non-Gaussianity of the observed A(Li) error distribution the discrepancy is reduced to 4.6σ, which is still significant.
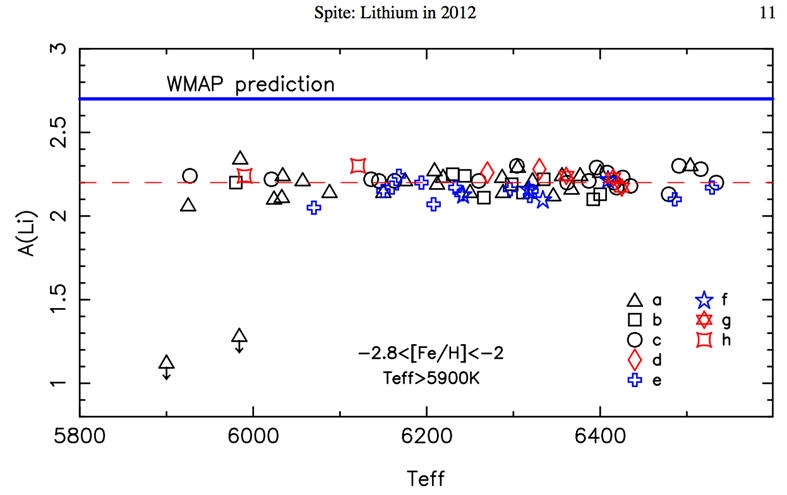
The 77 stars that our statistical analysis was based off of, from “Spite, Memorie della Societ\`a Astronomica Italiana Supplementi, 2012 Vol. 22, page 9”.
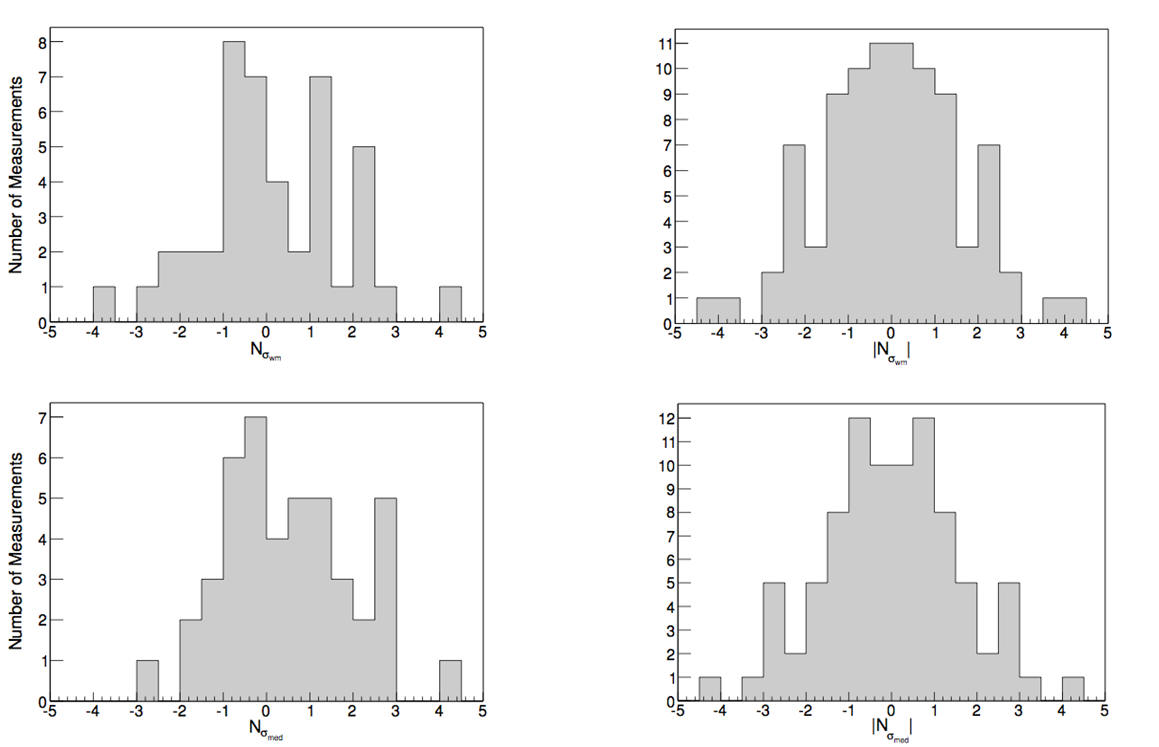
Distribution of both the Nσ obtained from median and weighted mean from the 44 points of from Spite et al. (2012).
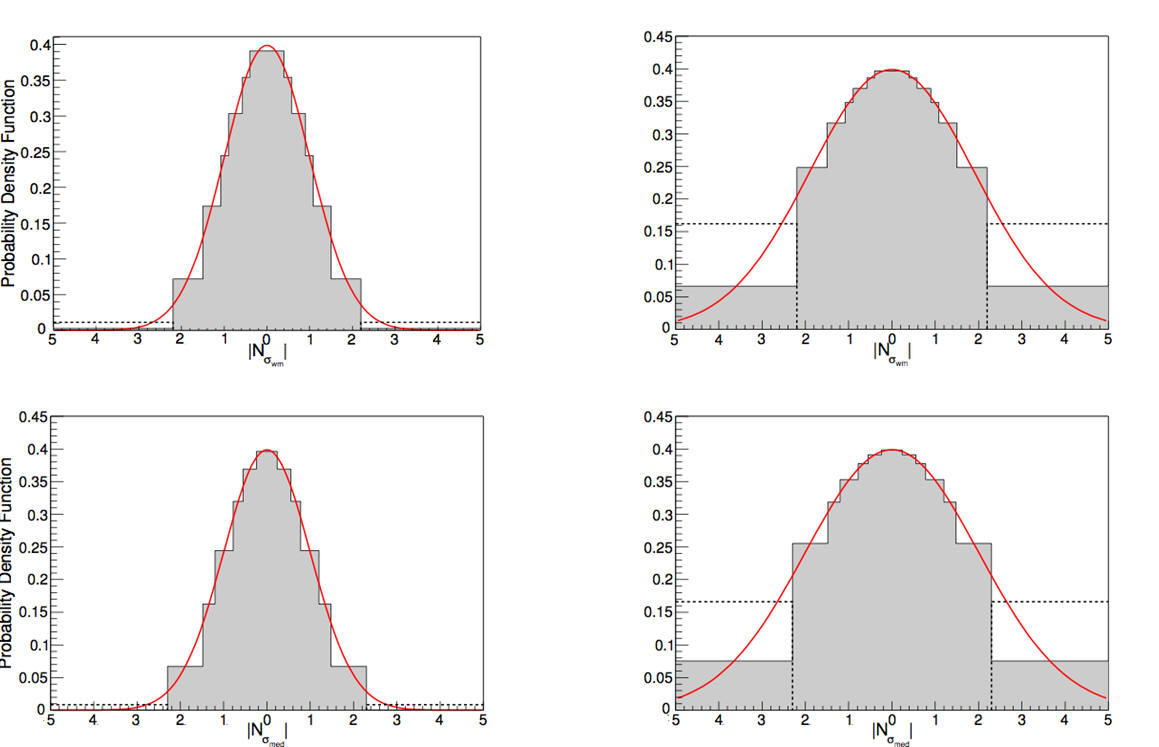
Gaussian probability density distribution functions.
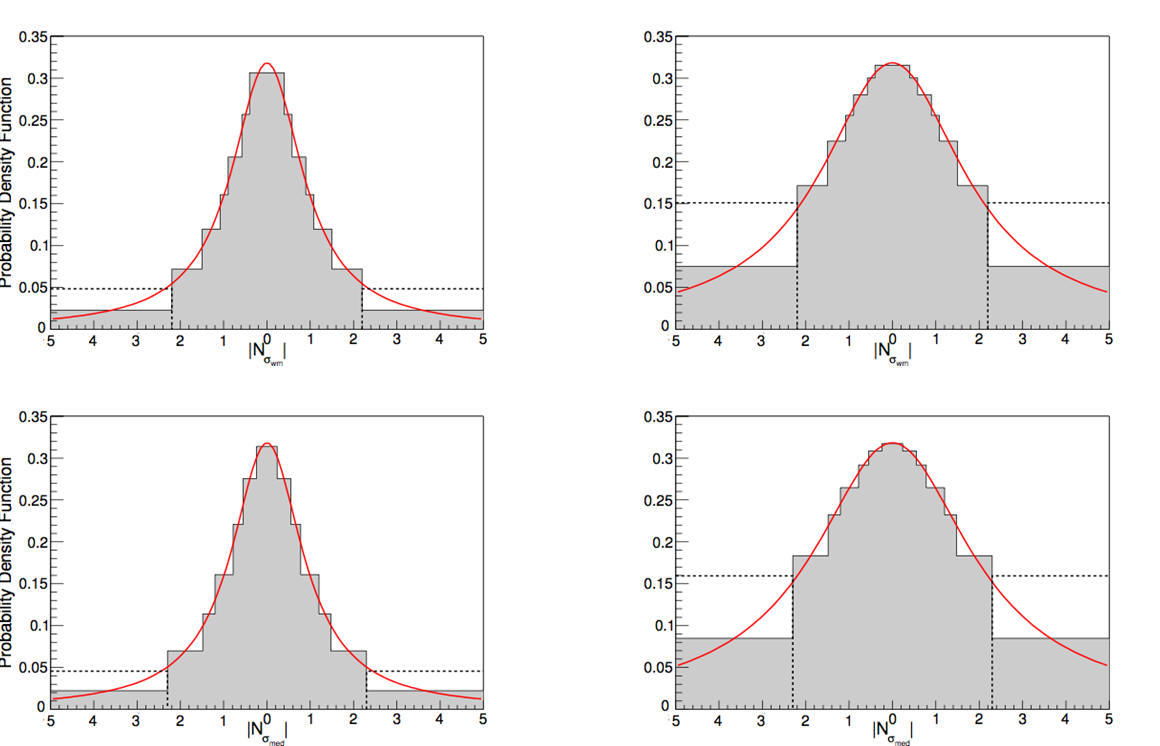
Cauchy probability density distribution functions.
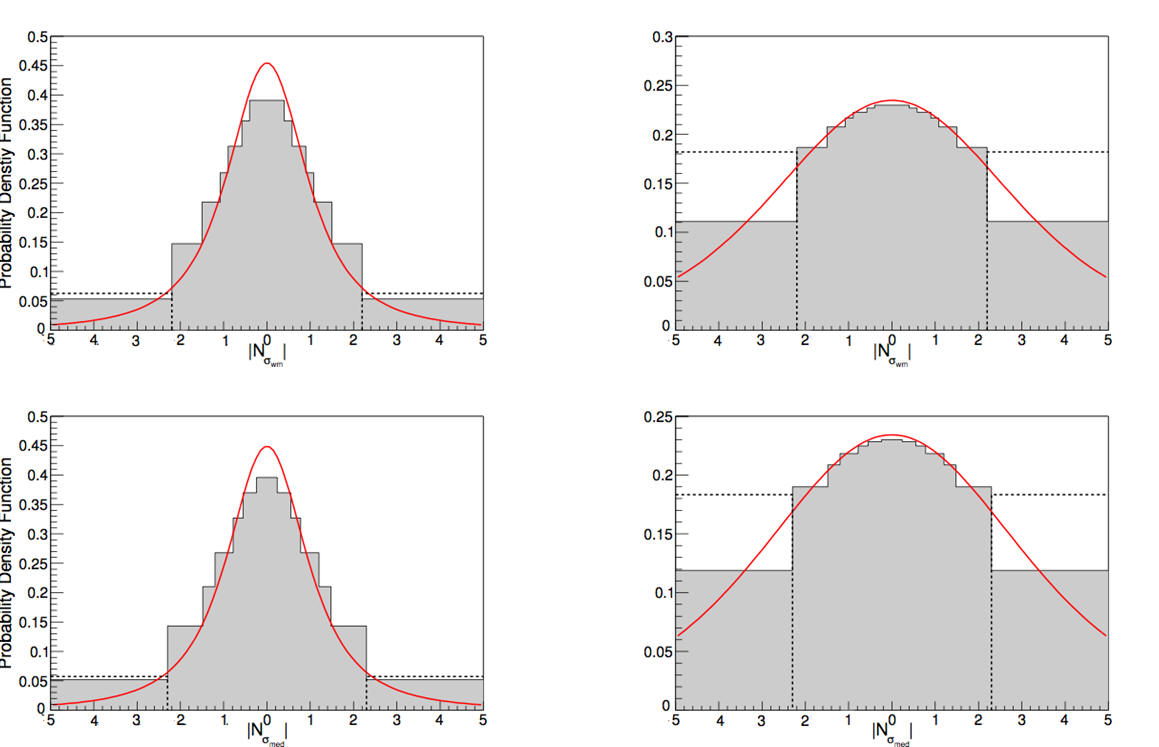
Student's t probability density distribution functions.
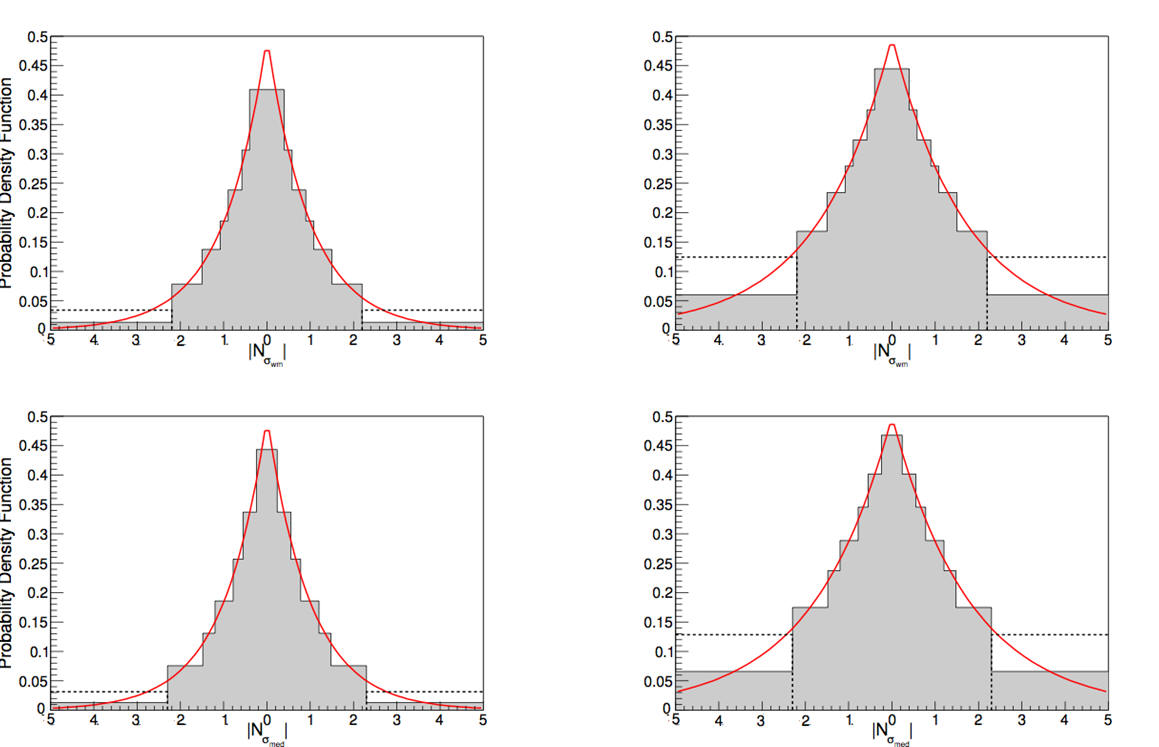
Double exponential probability density distribution function.
