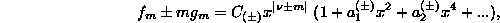
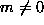modes the in-
and out-of-plane 
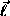oscillations are coupled strongly
near the vortex center. For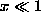 
(
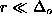) one
has the Taylor expansions
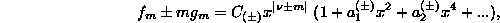
where the coefficients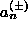 
are determined by 
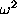and arbitrary parameters
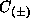. The presence of non-scale coefficient 
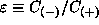is a special property of the eigenvalue
problem (6); the ratio of amplitudes of in- and
out-of-plane oscillations in the wave with given frequency
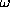is regulated by 
.
Far from the vortex core,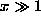 
, the coupling term in
(6) is exponentially small,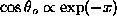 
.
For 
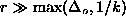the solution for g can be
expressed in the oscillating form (10). For
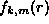one has asymptotics with linear combinations of
exponents like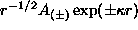 
, where
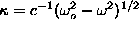, and constants
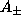depend on 
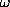and 
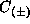. For
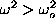only oscillating asymptotics like
(10) appear.
In the most interesting region of small frequencies,
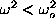, the eigenfunction with oscillations of
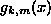combined with exponentially decaying 
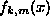can be constructed using the shooting method, ``killing'' the
growing exponent in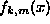 
by choosing an appropriate
value of 
. Numerically, the boundary condition
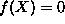was applied, and very well-pronounced exponential decay
of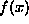 
resulted, even for 
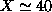. The scattering problem
can be analyzed from these calculations. In order to explain
let's consider the magnons without a vortex. The solutions can be
represented in the form (7) with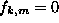 
,
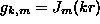, which is (10) with a defined
value of the phase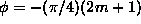 
. In the presence of
the vortex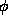 
takes another value, which means the asympotic
is in the form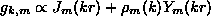 
, where
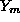is a Neumann function. Obviously, the coefficient 
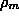is the measure of the intensity of scattering, see
Fig 4. Then, the S-matrix can be obtained from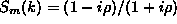 
. The values of 
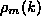are smaller for
larger values of m, for example,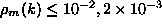 
and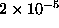 
for m=3,4 and 6.
It is well known that the presence of a quasi-local mode with
large lifetime at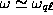 
gives a sharp
maximum in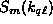 
, 
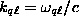. The
components of the S-matrix for all m's excluding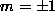 
have
no such maxima at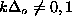 
, and the maximum for
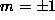is very wide. It means that there is no chance to have
a well-defined quasi-local mode at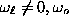 
for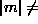 
1. However, at 
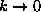, the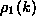 
dependence
is very fast, possibly indicating a root type singularity. The
eigenfunctions near this point have a special shape with a
well-defined maximum at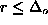 
, which is fitted by the
translational mode functions ( 
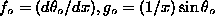,) and a small amplitude
oscillating tail. It means that the quasi-local mode with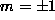 
, 
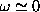is present, as in FMs.