Outline of selected topics for current and future research

Back to Home Page Related Jobs Publications

To those interested in collaborating with us: The following description of current research projects and anticipated future interests reveals a specific vision for the continuation and expansion of my research program in atomic, molecular, optical, and surface (AMOS) physics at KSU. Depending on the availability of funds, experimental advances, and intriguing new ideas my group is always open towards new and/or collaborative projects, in addition to the ones listed below.

To interested students: If you would like to know more about our research or are interested in working in my group, don’t hesitate to call or email me, or simply stop by my office. Whether you are new to research in theoretical AMOS physics or already have experience, I will find a topic of current research interest for you to work on.

Summary

In close collaboration with experimental groups and motivated in part by available and emerging intense short-pulse laser and X-ray light sources, my research group seeks to develop conceptual, analytical, and numerical tools for the theoretical description of the

a) coherent electronic dynamics in atoms and

b) coherent electronic and nuclear dynamics in molecules, clusters, and solid surfaces.

This research includes a number of projects that are sketched below. Their unifying theme is the study of dynamical processes at the natural time scale of either the electronic motion (attoseconds, 1as=10^-18s) or the nuclear motion in molecules (femtoseconds, 1fs=10^-15s). An important goal for our future research will be to combine this ultrahigh resolution in time with high spatial resolution at the intrinsic length scale (1 Angstøm) of matter.

Contents:

1. Nuclear dynamics of molecules in intense IR and XUV electric fields

1.1 Controlling the nuclear and electronic motion in molecules with short light pulses

1.1.1 Control schemes for manipulating the shape of nuclear vibrational wave packets

1.1.2 Dissociative ionization of H₂ in an attosecond pulse train and delayed laser pulse

1.1.3 Electron localization in molecular fragmentation of H₂ with CEP stabilized laser pulses

1.1.4 Laser control of the electronic motion and localization in H₂⁺ in phase space

1.2 Nuclear wave-packet dephasing and revivals in D₂⁺

1.3 Towards the complete imaging of molecular dynamics with laser and XUV pulses

1.3.1 Quantum-beat imaging of the vibrational nuclear dynamics in diatomic molecules

1.3.2 Quantum-beat imaging of the rotational-vibrational nuclear dynamics in diatomic molecules

1.4 Close-coupling calculations for H₂

1.5 Moving to larger molecules: Time-resolved fragmentation dynamics in N₂, O₂, and CO

2. Time-resolved electronic dynamics in atoms and complex systems

2.1 Attosecond time-resolved photoelectron spectroscopy of atoms

2.1.1 Coulomb-laser coupling effects in attosecond time-resolved photoelectron spectra

2.1.2 Streaking and Wigner time delays in photoemission from atoms

2.1.3 Attosecond time-resolved probing of instantaneous AC Stark shifts in helium atoms

2.1.4 Electron interference in atomic photoionization by a single few-cycle IR laser pulse

2.1.5 Time-resolved autoionization

2.2 Time-resolved electronic dynamics in complex systems

2.2.1 Attosecond time-resolved photoelectron spectroscopy of metal surfaces

2.2.2 Laser-assisted photoemission from adsorbate-covered metal surfaces:

Time-resolved core-hole relaxation dynamics from sideband profiles

2.2.3 Dynamical image-charge effects in streaked photoelectron spectra of metal surfaces

2.3 Electronic structure of flat and vicinal surfaces

2.4 Image-potential states of single- and multi-walled carbon nanotubes

3. Laser-assisted collisions

4. Highly correlated negative-ion resonances in photodetachment and electron scattering processes

1. Nuclear dynamics of molecules in intense IR and XUV electric fields

1.1 Controlling the nuclear and electronic motion in molecules with short light pulses

Project scope: To develop numerical and analytical tools to efficiently predict the effects of strong laser fields on the bound and free electronic and nuclear dynamics in small molecules. Furthermore, we seek to understand the degree to which the electronic motion in small molecules can be steered by laser pulses, e.g., leading to the localization of an electron near a given nucleus.

1.1.1 Control schemes for manipulating the shape of nuclear vibrational wave packets

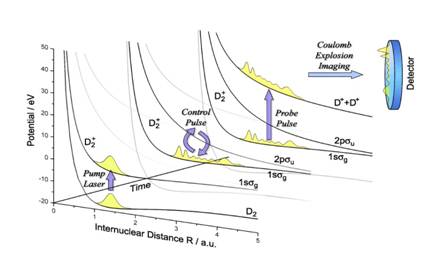
Recent progress: We investigated the dissociation and ionization of D₂ and D₂⁺ in short intense laser pulses by applying wave-packet propagation methods. In particular, we examined the possibility of manipulating the vibrational-state decomposition of bound vibrational wave packets with a sequence of short control laser pulses at minimal dissociative loss (Fig. 1).

Fig. 1. Ionization of D2 (ν=0) by a pump pulse, followed by the modification of the vibrational wave packet on the D2^+1sσg^+potential curve by a control pulse, and the final destructive analysis via Coulomb explosion imaging by a probe pulse.

Ionization of neutral D₂ molecules by a short and intense pump laser pulse may create a vibrational wave packet on the lowest (1sσ_g⁺) adiabatic potential curve of the D₂⁺ molecular ion [1,2]. We showed numerically that a single ultra–short intense near-infrared (800 nm) control pulse with an appropriate time delay can strongly quench the vibrational-state distribution of the nuclear wave packet by increasing the contribution of selected stationary vibrational states of D₂⁺ to more than 50% [3]. We found that a second identical control pulse with a carefully adjusted delay can further squeeze the vibrational state distribution, likely without dissociating the molecular ion, thereby suggesting a multi–pulse control protocol for generating (almost) stationary excited nuclear wave functions (Fig. 2). The quality of this Raman–control mechanism can be tested experimentally by Coulomb-explosion imaging, i.e., by fragmenting the molecular ion with a probe pulse and by identifying the nodal structure of the surviving vibrational state in the kinetic-energy-release (KER) spectrum of the molecular fragments [1-4].

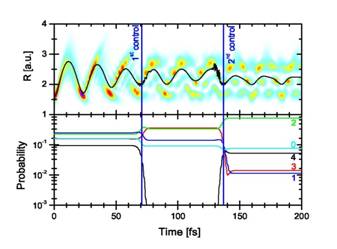
Fig. 2. Top: Time evolution of the nuclear wave function probability density as a function of the internuclear distance R for two 6 fs, 10^14 W/cm^2 control pulses with delay times of τ1=70.7 fs and τ2=136.8 fs relative to the launch time (t=0). The superimposed curve shows the expectation value <R>. Bottom: Time evolution of a few stationary-vibrational-state contributions to the wave packet.

We compared results for our H₂⁺ model calculations that only include the lowest two coupled adiabatic potential curves [3] with new full 3D calculations [5] and examined the possibility of manipulating the vibrational-state decomposition of bound vibrational wave packets with a sequence of up to eight control laser pulses at minimal dissociative loss. We find that the precise timing between pump and control-laser pulses allows the direct manipulation of the final vibrational state composition and dissociation dynamics of the molecular ion. We showed that a significant enhancement of the occupation of particular vibrational stationary state contributions can be achieved for laser intensities below the onset of strong ionization.

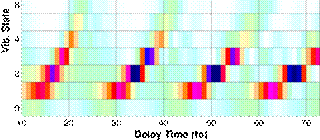
Fig. 3. Stationary vibrational-state composition of an initial Franck-Condon nuclear wave packet in D2^+ after exposure to a 6 fs 0.1 PW/cm^2 Gaussian control pulse as a function of the control-pulse delay.

We found that a sequence of short control pulses can effectively steer the nuclear motion in D₂⁺ molecular ions and, depending on the control-pulse delays, even stop a moving nuclear wave packet to produce an excited stationary vibrational state (Fig. 3).

Future plans: Control schemes for quenching moving ro-vibrational wave packets into stationary states using a sequence of control pulses will be further examined and adjusted to model experimental conditions as closely as possible.

Collaborators: Thomas Niederhausen, Fernando Martin (University of Madrid, Spain)

[1] B. Feuerstein and U. Thumm, Phys. Rev. A 67, 043405 (2003).

[2] B. Feuerstein and U. Thumm, Phys. Rev. A 67, 063408 (2003).

[3] T. Niederhausen and U. Thumm, Phys. Rev. A 77, 013407 (2008).

[4] B. Feuerstein and U. Thumm, J. Phys. B 36, 707 (2003).

[5] T. Niederhausen, U. Thumm, and F. Martin, submitted to Phys. Rev. A.

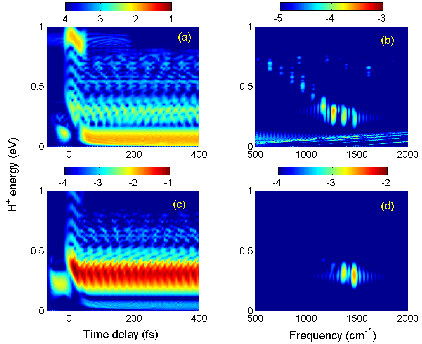
1.1.2 Dissociative ionization of H₂ in an attosecond pulse train and delayed laser pulse

Recent progress: The ionization of H₂ in a single attosecond XUV pulse (SAP) generates a nuclear wave packet in H₂⁺ which is entangled with the emitted photoelectron wave packet. The nuclear wave-packet dynamics can be observed by dissociating H₂⁺ in a delayed IR laser pulse. If H₂⁺ is ionized by a sequence of XUV pulses of an attosecond pulse train (APT) (Fig. 1), whether or not the corresponding sequence of nuclear wave packets in H₂⁺ is detected as a coherent or incoherent superposition depends on whether and how the photoelectrons are observed. We simulated the nuclear dynamics in this XUV pump - IR probe scenario and analyzed our numerical results for both, single attosecond pump pulses and pump-pulse trains of different lengths and temporal spacings between individual XUV pulses. By superimposing nuclear wave packets in H₂⁺ generated by individual pulses in the pump-pulse train incoherently, we calculated proton kinetic energy release (KER) spectra [1] in good qualitative agreement with the experiment in reference [2].

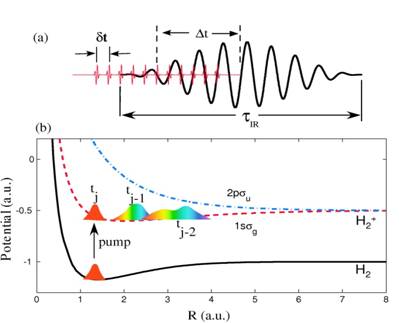
Fig. 1. (a) Schematic of the APT and IR laser field. The time delay Δt is the offset between the centers of the APT and IR pulses. The pulse duration of the IR pulse is τIR, and the separation between subsequent attosecond pulses is Δt. (b) Relevant Born-Oppenheimer potential curves of H2 and H2^+. A sequence of nuclear vibrational wave packets is generated on the 1sσg electronic ground state potential curve of H2^+ by repeated ionization of H2 in subsequent XUV pulses of the APT.

Since photoelectrons carry phase information, the degree of coherence in the observed KER in an APT - delayed IR pulse experiment will change if photoelectrons are detected in coincidence with molecular fragments. Without the observation of coincident photoelectrons, we anticipate the KER to be devoid of coherence effects between subsequently launched nuclear wave packets, whereas coherence effects are expected to be most prominent if photoelectrons are detected in extremely narrow momentum bins and coincident with molecular fragments [1].

Future plans: We anticipate refined experiments in which protons and XUV-pulse-emitted electrons are detected in coincidence. Assuming that such experiments can be carried out with sufficiently large count rates, we predict an interesting transition from an incoherent to a coherent superposition of nuclear wave packets by recording photoelectrons in increasingly narrower momentum bins. For the coherent proton KER spectra, we find an extremely sensitive dependence on the IR wavelength, that might be exploited to characterize the IR laser pulse in terms of interference effects (in both delay and proton energy) in fragment KER spectra (Fig. 2). With regard to future numerical simulations, even for the simplest molecule, H₂, more work is needed in order to establish a firm lower limit for the effect of nuclear wave packet interferences on KER spectra [1].

Fig. 2. Time-dependent proton energy distributions (left column) and corresponding power spectra (right column) for H2 exposed to an APT and a delayed 30-cycle IR laser pulse with a peak intensity of 10^13 W/cm^2. The APT consists of 14 alternating attosecond XUV pulses. Maximal coherence is assumed for the superposition of individual H2^+ nuclear wave packets. (a) and (b): Results for an IR carrier wavelength of λIR=800nm. (c) and (d): Results for λIR =727nm.

Collaborator: Feng He (SJTU Shanghai, PRC)

[1] F. He and U. Thumm, Phys. Rev. A 81, 053413 (2010).

[2] F. Kelkensberg et al., Phys. Rev. Lett. 103, 123005 (2009).

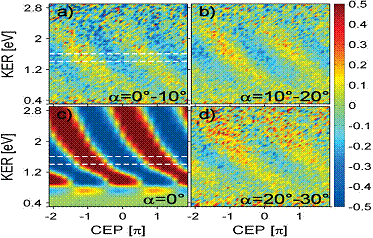
1.1.3 Electron localization in molecular fragmentation of H₂ with CEP stabilized laser pulses

Recent progress: Fully differential data for H₂ dissociation in ultrashort (6fs, 760nm), linearly polarized, intense (0.44 PW/cm²) laser pulses with a stabilized carrier-envelope-phase (CEP) were recorded with a reaction microscope. Depending on the CEP, the molecular orientation, and the KER, asymmetric proton emission at low KERs (0–3 eV) was measured [2] to be much stronger than reported by previously [1]. Our wave packet propagation calculations [2] reproduce the salient features and discard, together with the observed KER-independent electron asymmetry, the first ionization step as the reason for the asymmetric proton emission (Fig. 1).

Future plans: Even though the asymmetry in the experiment [2] shows a similar CEP and KER-dependence as in [3], the physical situation considered there, an incoherent sum of vibrational states, is different. Instead, for the experimental conditions in [2], a wave packet is produced in the first step [4,5], pointing to the possible control of chemical reactions through attosecond steering of electrons in a new type of ‘‘pump-control’’ experiment. Switching on the control laser at a time when the wave packet approaches the (non-adiabatic) coupling region should strongly enhance population transfer and asymmetry contrast. In this case control can be achieved very efficiently by changing the pump-probe-delay, i.e., by guiding nuclear wave packets through coupling regions where CEP stabilized pump-control schemes steer the electronic motion on a sub-femtosecond time scale.

Fig. 1. Dissociation asymmetry in dependence of the KER and the CEP for proton emission angles between (a) 0–10, (b) 10–20, and (d) 20–30 degrees with respect to the laser polarization axis. (c) Time-dependent Schrödinger equation calculations. Since only relative CEPs were measured, the axes of the experimental data were shifted to fit the calculation.

Collaborators: Bernold Feuerstein and authors of ref. [2] (MPIK, Heidelberg, Germany)

[1] M. F. Kling et al., Science 312, 246 (2006).

[2] M. Kremer, B. Fischer, B. Feuerstein, V. L. B. De Jesus, V. Sharma, C. Hofrichter, A. Rudenko, U. Thumm, C. D. Schröter, R. Moshammer, and J. Ullrich, Phys. Rev. Lett. 103, 213003 (2009).

[3] J. J. Hua and B. D. Esry, J. Phys. B 42, 085601 (2009).

[4] M. Winter, R. Schmidt, and U. Thumm, Phys. Rev. A 80, 031401(R) (2009).

[5] M. Winter, R. Schmidt, and U. Thumm, New J. of Phys. 12, 023023 (2010).

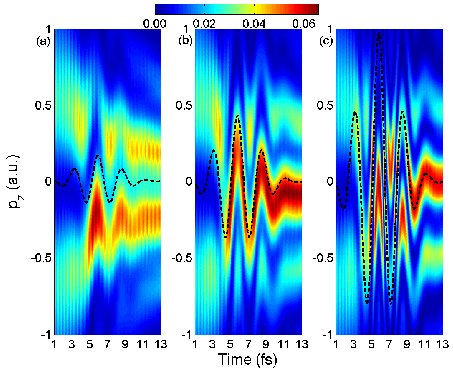
1.1.4 Laser control of the electronic motion and localization in H₂⁺ in phase space

Recent progress: The electronic dynamics in a molecule driven by a strong laser field is complex and in part even counterintuitive. As a prototype example, we have studied the electronic motion inside dissociating H₂⁺ molecules that are exposed to a fs IR laser pulse [1]. The sensitive dependence of the correlated electronic-nuclear motion can be explained in terms of the electronic momentum distribution of the dissociating molecule. This distribution is dynamically modulated by the nuclear motion and periodically shifted in the oscillating IR electric field, leading to strong-field-modulated diffraction effects in the correlated electronic-nuclear motion in dissociating molecular ions (Fig. 1). Depending on the IR-laser intensity, the direction of the electronic motion can follow or oppose the IR-laser electric force.

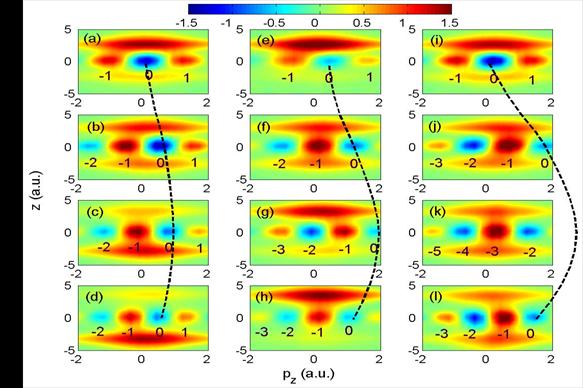
Our interpretation of this effect in terms of a Wigner phase-space distribution [1] is based on the passage of electronic flux through diffractive “momentum gates” of the two-center system that may or may not allow the electron to transfer to the other nucleus (Fig. 2). It reveals that the oscillating vector potential of the IR laser field periodically shifts these gates, directing the electron through different gates at different laser intensities. These results show how the internal electron dynamics in H₂⁺ is driven by both the external laser field and diffraction effects.

Fig. 1. Electron momentum distribution along the laser polarization during the dissociation of H2^+ in a 5.3 fs IR laser pulse with a time delay of 5.8 fs and intensities of (a) 3x10^12, (b) 2x10^13, and (c) 10^14 W/cm^2. Dashed lines indicate the classical free-electron momentum in the IR field, assuming zero initial momentum. The dissociating wave packet was launched from the initial 1sσg onto the 2pσu state of H2^+in a resonant single-photon transition, induced by a 2-cycle, 106 nm, 10^13W/cm^2 attosecond Gaussian pump pulse.

Fig. 2 Wigner distribution for IR laser intensities of 3x10¹² (left), 2x10¹³ (middle) and 10¹⁴ W/cm² (right column) and time delays of 4.5, 5.2, 5.8, and 6.5 fs (from the top to the bottom row). The dashed lines indicate IR-laser-driven oscillations of the momentum gate that was initially centered at p_z = 0.

Future plans: We intend to further investigate the control - at a sub-fs time scale - of the internuclear electronic dynamics in small molecules by tuning (IR) laser parameters. Next, we plan to investigate the dynamics and control of electronic motion at a sub-fs time scale in other molecules, including highly symmetrical large molecules (C₆₀).

Collaborators: Feng He (KSU and SJTU Shanghai, PRC), Andreas Becker (JILA, Boulder, CO)

[1] F. He, A. Becker, and U. Thumm, Phys. Rev. Lett. 101, 213002 (2008).

1.2 Nuclear wave-packet dephasing and revivals in D₂⁺

Project scope: To characterize the laser-excited bound motion of coherent nuclear wave packets in small molecules in terms of decoherence, dephasing, revivals, and competing dissociation, and to help with the interpretation of recent experiments.

Recent progress: Fast ionization of neutral D₂ in an intense laser pulse leads to the formation of molecular ions in a coherent superposition of excited (ro-)vibrational states, i.e., to a moving nuclear (ro-)vibrational wave packet. Typically, after a few optical periods, the anharmonicity of the potential curve results in the collapse of the wave packet due to the dephasing of its stationary vibrational-state components.

(c) (c) Fig. 1. Coherent motion of the nuclear vibrational wave packet in and dissociation of D2^+. (a) Probability density and expectation value <R> of the internuclear distance. (b) Autocorrelation function. (c) Measured kinetic energy release, showing quarter and half revivals [3].

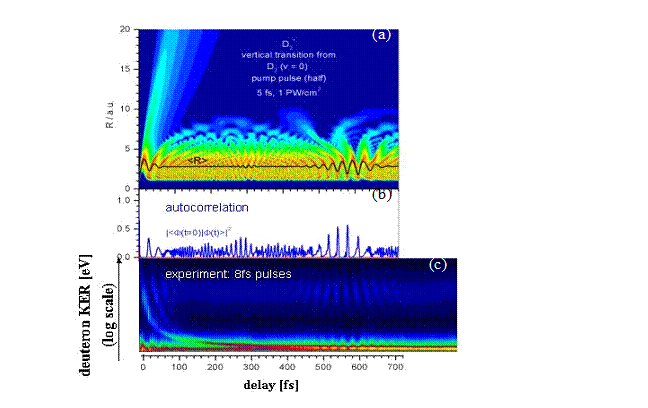Figure 1a and b illustrates our reduced-dimensionality calculations [1,2] for the nuclear wave-packet dynamics in D₂⁺ following ionization of D₂ (v = 0) in a 5 fs, 10¹⁵ W/cm² pulse. After a few optical cycles, the wave packet collapses due to the dephasing of its stationary vibrational state components. The evolution of the nuclear probability density (Fig. 1a) and autocorrelation function (Fig. 1b) shows revivals of the wave packet 100 and 200 optical cycles, respectively, after the wave packet has been launched. A second laser pulse, short and strong enough to ensure instantaneous and complete ionization of D₂⁺, can probe the time evolution of the wave packet. Pump-probe experiments with 8 fs laser pulses on D₂ recorded the delay-dependent kinetic energy release of the deuteron fragments [3,4] and reproduce the first half and full wave packet revivals of our model calculation (Fig. 1c).

Future plans: For delays beyond the first full revival, the comparison between theory and the experiments becomes inconclusive. Since this discrepancy appears only for delays that are longer than 1ps, it is currently not known whether it is caused by insufficient experimental resolution or originates solely from the onset of rotational dephasing. We intend to more carefully investigate the long-term revival structures in D₂⁺. Initially, we will improve our (linear) reduced dimensionality model by increasing the number of electronic degrees of freedom. In addition, we intend to relax our assumption that the initial wave function is a coherent superposition of vibrational states with simple Franck-Condon weight factors. At a later stage, we anticipate using results of calculations for neutral D₂ molecules in order to include a realistic pump-pulse-dependent description of the generation of a (non-Franck Condon) wave packet in D₂⁺. In order to understand long-term revivals at the ps time scale, i.e., the interplay of vibrational and rotational revivals, we will include the rotational motion of the molecule in our calculation.

Collaborators: Bernold Feuerstein (MPIK, Heidelberg, Germany)

[1] B. Feuerstein and U. Thumm, Phys. Rev. A 67, 043405 (2003).

[2] B. Feuerstein and U. Thumm, Phys. Rev. A 67, 063408 (2003).

[3] T. Ergler et al., Phys. Rev. Lett. 97, 193001 (2006).

[4] A. Rudenko et al., Chemical Physics 329, 193 (2006).

1.3 Towards the complete imaging of molecular dynamics with laser and XUV pulses

Project scope: We seek to develop numerical and analytical tools to fully image the nuclear dynamics in small molecules.

1.3.1 Quantum-beat imaging of the vibrational nuclear dynamics in diatomic molecules

Recent progress: In a proof-of-principles effort, we introduced an internuclear-distance (R) -dependent harmonic imaging technique that allows vibrational beat frequencies, molecular potential curves, and the nodal structure of nuclear wave functions to be derived from measured kinetic-energy-release (KER) spectra. In this method, the time-resolved KER spectra of vibrating and dissociating D₂⁺ molecules are studied in comparison with the R-dependent harmonic analysis of the corresponding wave packets [1, 2].

Our calculations demonstrate that the obtained two-dimensional R-dependent frequency spectra enable the characterization of the wave-packet dynamics and directly visualize the field-modified molecular potential curves in intense, ultra-short laser pulses [1], including “bond softening” and “bond hardening” processes [3]. Figure 1 shows examples of this imaging scheme for the complete mapping of molecular potential curves for the fundamental deuterium molecular ion, for laser-free propagation of D₂⁺ nuclear wave packets (Fig. 1a) and including the interaction with a laser electric field (Fig. 1b). These examples show how the molecular potential and its bound vibrational wave function are modified by the added laser field.

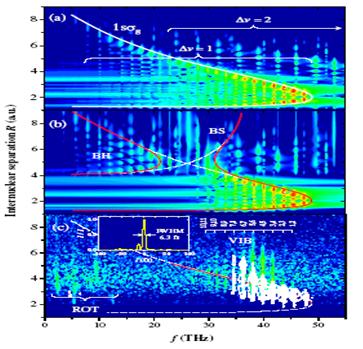
Fig. 1. Power spectrum |w(R,f)|^2 as function of the quantum-beat frequency f and R for a sampling time of T=3 ps. (a) Numerical field-free wave packet propagation of an initial Franck-Condon distribution. (b) As (a) but with a 50 fs pedestal of 0.01 PW/cm^2 preceding the probe pulse causing “bond softening” (BS) and “bond hardening” (BH). (c) Experimental distribution extracted from coincident D^+ pairs with vibrational (VIB) and rotational (ROT) contributions. White contours: numerical results using the actual laser pulse profile shown in the inset.

Our method relies on the Fourier transformation, w(R,f), over a sampling time T of the time- and R-dependent probability density w(R,t) of the D₂⁺ nuclear wave packet. Applied to numerically propagated D₂⁺ vibrational wave packets, it allows us to simulate the outcome of novel experiments. The simulated experiments are assumed to be based on the Coulomb-explosion mapping of pump-probe-delay (τ)-dependent KER spectra and subsequent R-dependent harmonic analysis for finite T (0 < τ < T). First experimental results [2], shown in Fig. 1c, reproduce the known vibrational beat frequencies f and retrace the outer part of the potential well. So far, the inner part of the potential well could not be observed due to suppressed ionization rates at small R.

Collaborators: Bernold Feuerstein, Robert Moshammer, Joachim Ullrich (MPIK, Heidelberg, Germany)

[1] U. Thumm, T. Niederhausen, and B. Feuerstein, Phys. Rev. A 77, 063401 (2008).

[2] B. Feuerstein, T. Ergler, A. Rudenko, K. Zrost, C.D. Schröder, R. Moshammer, J. Ullrich, T. Niederhausen, and U. Thumm, Phys. Rev. Lett. 99, 153002 (2007).

[3] M. Magrakvelidze, F. He, T. Niederhausen, I. V. Litvinyuk, and U. Thumm, Phys. Rev. A 79, 033410 (2009).

1.3.2 Quantum-beat imaging of the rotational-vibrational nuclear dynamics in diatomic molecules

Recent progress: We investigated the extent to which measured time-dependent fragment KER spectra and calculated nuclear probability densities can reveal i) transition frequencies between stationary vibrational states, ii) stationary rotational states and ro-vibrational (RV) couplings, iii) the nodal structure of stationary rotational and vibrational states, iv) field-free and laser-field-dressed adiabatic electronic potential curves of the molecular ion, and v) the progression of decoherence induced by random interactions with the environment [1-4].

By solving the TDSE in full dimensionality, we simulated the coherent evolution of ro-vibrational nuclear wave packets and discussed their ro-vibrational dynamics in D₂⁺ [4,5] (Fig. 1) . Our imaging method is based on the Fourier transformation, w(R, θ, f), over finite sampling times T, of the time-, internuclear distance (R)-, and molecular orientation (θ)- dependent probability density w(R, θ, t) of nuclear wave packet [3,4]. Our numerical results for ro-vibrational wave packets demonstrate that the obtained two-dimensional R-dependent power spectra enable the comprehensive characterization of the wave-packet dynamics and directly visualize the laser-modified molecular potential curves in intense, including `bond softening' and `bond hardening' processes [1,4,5] (Fig.s 2 and 3). This harmonic-time-series analysis also leads to a general scheme for the full reconstruction, up to an overall phase, of the initial wave packet based on measured KER spectra [3].

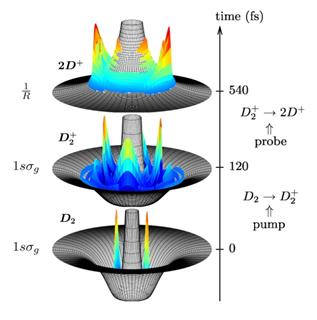
Fig. 1. Snapshots of the calculated time evolution of a ro-vibtational nuclear wave packet in D2^0,+,2+. Bottom: At t=0 a pump laser pulse ionizes D2 and excites the initial RV wave packet from the 1sσg, ν=0 state in D2 (bottom graph) to the 1sσg state of D2^+ where it evolves, continuously changing its distribution in R and θ. Middle: Probability density of the wave packet in D2^+ at t=120 fs. Ionization by a probe laser pulse after a delay of, e.g., τ=540 fs projects the wave packet onto the repulsive potential surface of the 2D^+-system (top graph), leading to fragmentation by CE. Top: Measurement of the KER of the D^+ fragments as a function of τ enables the characterization of the wave packet dynamics in terms of R- and θ-dependent spectra.

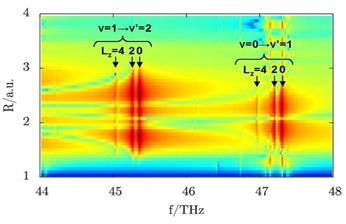
Including rotation of the molecular ion (Fig. 2) [4,5], quantum-beat frequencies that correspond to a vibrational transition ν→ν’ are split into multiple lines due to rotational-vibrational coupling. These lines represent individual angular-momentum contributions to the ro-vibrational wave packet (Fig. 2).

Based on numerical examples for the nuclear dynamics without and under the influence of pulsed and continuum-wave (cw) laser light, we discussed and quantified i) the signature of RV couplings in quantum-beat spectra and ii) to what extent the quantum-beat analysis of measured time-dependent fragment kinetic energy release spectra is expected to image the laser-dressed RV structure of D₂⁺ (Fig. 3).

Fig. 2. Angle-integrated power spectra A(R,f) = |∫dθ w(R,θ,f)|^2 for D2^+ as a function of the beat frequency f and internuclear distance R. Due to ro-vibrational couplings, lines for the same vibrational transition and different angular momenta Lz do not coincide. Vibrational transitions at larger Lz appear at lower frequencies.

Future plans: We intend to simulate the extent to which the quantum-beat analysis of measured time-dependent fragment KER spectra can quantify the laser-modulated ro-vibrational structure of H₂⁺ and other diatomic molecules. Extending this technique to more complicated polyatomic molecular systems and reaction complexes may enable the investigation of molecular dynamics across the (field-modified) potential barrier along a particular reaction coordinate, and, thus, provide a basis for novel multidimensional optical-control schemes for chemical reactions. We also envision to apply this method to quantify the progression of decoherence in the nuclear motion based on a time series of KER spectra.

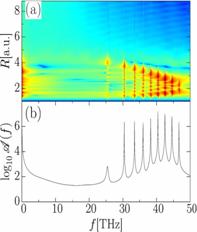
Fig. 3. (a,c) Angle-integrated power spectrum A(R,f). (e) Internuclear-distance-integrated power spectrum W(θ, f) = |∫dR w(R,θ,f)|². (b,d,f) Corresponding spectral line intensities for the evolution of (a,b) aligned and (c-f) rotating D₂⁺ molecular ions in a 10¹³ W/cm² cw laser field.

Collaborators: Rüdiger Schmidt, Martin Winter (Technical University Dresden, Germany)

[1] M. Magrakvelidze, F. He, T. Niederhausen, I. V. Litvinyuk, and U. Thumm, Phys. Rev. A 79, 033410 (2009).

[2] B. Feuerstein, T. Ergler, A. Rudenko, K. Zrost, C.D. Schroeder, R. Moshammer, J. Ullrich, T. Niederhausen, and U. Thumm, Phys. Rev. Lett. 99, 153002 (2007).

[3] U. Thumm, T. Niederhausen, and B. Feuerstein, Phys. Rev. A 77, 063401 (2008).

[4] M. Winter, R. Schmidt, and U. Thumm, Phys. Rev. A 80, 031401(R) (2009).

[5] M. Winter, R. Schmidt, and U. Thumm, New J. of Phys. 12, 023023 (2010).

1.4 Close-coupling calculations for H₂

Project scope: To investigate the simultaneous vibrational excitation and ionization of H₂ in a strong laser pulse by means of close-coupling calculations.

Outline: We are in the process of modeling the interaction of neutral H₂ with strong few-cycle IR laser pulses within a close-coupling calculation that retains the adiabatic Born-Oppenheimer potential energy curves V_i (R), i=1...3, for the electronic ground state of H₂ and the ground and first exited states of H₂⁺. We plan to solve the time-dependent Schrödinger equation, including all off-diagonal electric dipole couplings μ_ij, i,j=1...3, between the adiabatic electronic states. This approach describes the coupled propagation of vibrational wave packets in H₂ and H₂⁺. The wave packets in H₂⁺ are due to the ionization of H₂ while complementary wave packets in H₂ are generated by “hole burning” [1]. The process of hole burning is due to the predominant ionization of H₂ at larger internuclear distances that transforms the initial stationary vibrational ground state of H₂ into an outward moving wave packet.

These close-coupling calculations are incomplete in the sense that they do not resolve the motion of the ionized electron(s) and thus require additional model assumptions for the dipole couplings. We intend to investigate the prospect for conducting– at reasonable numerical expense – improved close-coupling calculations that include electronic and nuclear degrees of freedom. To guide us through these technically complex investigations of the dissociative (single and double) ionization of H_2, we view single- and double ionization of the laser-plus-molecule system as Feshbach resonances that can be parameterized in terms of Fano-resonance parameters. Numerical applications will start with a limited basis consisting of the two lowest Born-Oppenheimer electronic states of the molecular ion. We plan to proceed by first modeling the bound-continuum couplings in terms of appropriate parameters, and to continue with explicit calculations of the coupling matrix elements. A serious challenge in the last step will be the adequate representation of the electronic continuum in terms of discretized continuum wave functions. Here, we will first explore the use of Weyl wave packets [2]. Our next goal is to repeat this sequence of steps for neutral molecules, including two electronic continua and three electronic potential curves, adding the ground-state potential curve of the neutral molecule.

[1] T. Niederhausen and U. Thumm, Phys. Rev. A 77, 013407 (2008).

[2] B. Bahrim und U. Thumm, Surf. Sci. 521, 84 (2002).

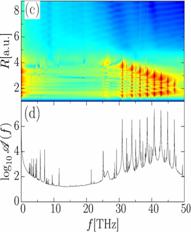
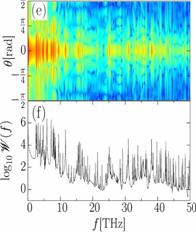
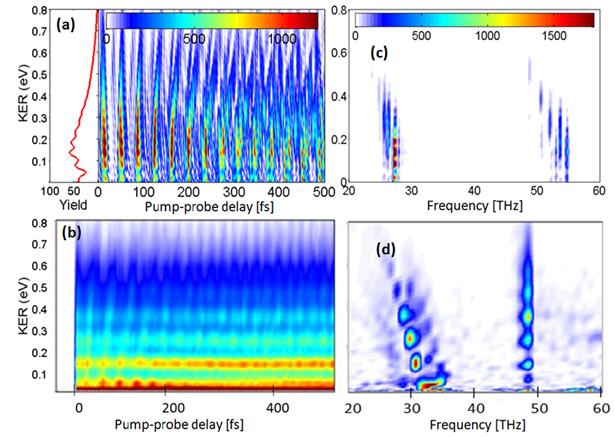
1.5 Moving to larger molecules: Time-resolved fragmentation dynamics in N₂, O₂, and CO

Project scope: To develop analytical and numerical tools to efficiently predict the effects of strong laser and XUV fields on the bound and dissociative nuclear dynamics in heavy diatomic molecules.

Recent progress: We investigated the nuclear dynamics of electronically and vibrationally excited heavy diatomic molecular ions by applying intense ultrashort IR probe pulses and measuring the KER spectra as a function of the pump-probe delay [1-4]. To analyze these spectra, we performed wave-packet-propagation calculations on adiabatic molecular potential curves (Fig. 1). First, to identify relevant transiently populated electronic states of the molecular ions, we modeled the pump step in Franck-Condon approximation and calculated the time evolution of initial vibrational wave packets separately for selected molecular potential curves.

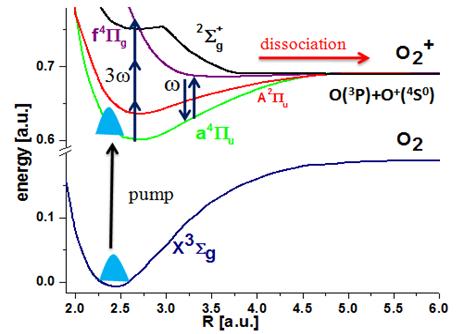
Fig. 1. Schematics for the mapping of the nuclear dynamics in oxygen molecular ions. The pump-laser pulse launches a nuclear wave packet onto the O2^+ potential curves a^4Пu and f ^4Пg by ionizing O2. After a variable time delay, an intense short probe pulse can cause dissociation of the molecular ion through one or net two photon processes.

The comparison of calculated KER spectra as a function of delay, quantum-beat frequency, and vibrational revival times for one adiabatic curve at a time with experimental spectra served us as a guide for selecting relevant electronic states of the molecular ions. Next, we included probe-laser-induced dipole couplings between the relevant molecular potential curves and compared the improved calculated KER spectra with experimental data, in an attempt to reveal non-adiabatic effects in measured KER spectra (Fig. 2). We employed the quantum chemistry code GAMESS [5] to calculate molecular potential curve and dipole couplings between them [4].

Future plans: Measured delay-dependent KER spectra of heavy diatomic molecules are difficults to simulate theoretically and are not well understood. We believe that the simultaneous study of measured and simulated KER spectra in both, time and energy domains provides a powerful tool that we intend to refine in order to disentangle the complicated ro-vibrational nuclear dynamics of laser-excited (and ionized) molecules [4].

Fig. 2 (a,c) Calculated and (b,d) measured [4] KER spectra for O₂⁺ as a function of (a,b) pump-probe delay and (c,d) quantum-beat frequency f. Calculated KER spectra include dipole-coupling of the a ⁴П_u and f ⁴П_g states by the 15 fs probe laser pulse with 3x10¹⁴ W/cm²peak intensity. (c,d) Power spectra obtained with a sampling time of 2 ps.

Collaborators: Maia Magrakvelidze, Lew Cocke, Itzik Ben-Itzhak (KSU), and authors of ref.s [1-4]

[1] S. De, I. Bocharova, M. Magrakvelidze, D. Ray, W. Cao, B. Bergues, U. Thumm, M. F. Kling, I. V. Litvinyuk, and C. L. Cocke, Phys. Rev. A 82, 013408 (2010).

[2] I.A. Bocharova, A. S. Alnaser, U. Thumm, T. Niederhausen, D. Ray, C.L. Cocke, and I.V. Litvinyuk, Phys. Rev. A 83, 013417 (2011).

[3] M. Magrakvelidze, F. He, T. Niederhausen, I. V. Litvinyuk, and U. Thumm, Phys. Rev. A 79, 033410 (2009).

[4] S. De, M. Magrakvelidze, I. Bocharova, D. Ray, W. Cao, I. Znakovskaya, H. Li, Z. Wang, G. Laurent, U. Thumm, M. F. Kling, I. V. Litvinyuk, I. Ben-Itzhak, and C. L. Cocke, Phys. Rev. A, accepted for publication (Sept. 2011).

[5] M. W. Schmidt et al., J. Comput. Chem. 14, 1347 (1993).

2. Time-resolved electronic dynamics in atoms and complex systems

We model the time-resolved IR-laser-assisted XUV photoelectron emission and Auger decay in pump-probe-delay-dependent streaking experiments with atoms and complex targets, such as clusters, carbon nanotubes, and surfaces.

2.1 Attosecond time-resolved photoelectron spectroscopy of atoms

2.1.1 Coulomb-laser-coupling effects in attosecond time-resolved photoelectron spectra

Project scope: To quantify and understand the effect of the Coulomb interaction between the photoelectron and residual ion on the photoemission dynamics and photoemission time delay.

Recent progress: Photoionization by attosecond XUV pulses into the laser-dressed continuum of the ionized atom is commonly approximated in strong-field approximation (SFA), i.e., by neglecting the Coulomb interaction between the emitted photoelectron and the residual ion [1,2,3]. By solving the time-dependent Schrödinger equation (TDSE), we identified a temporal shift δτ in streaked photoemission spectra that is due to the Coulomb-laser coupling in the final-state and exceeds 50 as at small photoelectron kinetic energies (Fig. 1). We expect the examination of this shift to enable (i) the experimental scrutiny of effects that are due to the combined action of Coulomb and laser forces on the photoelectron and (ii) tests of theoretical approximations to the exact Coulomb-Volkov state of the photoelectron. Within an eikonal (semiclassical) approximation, we derived an analytical expression for this effect and assessed its accuracy in comparison with full TDSE numerical results [4].

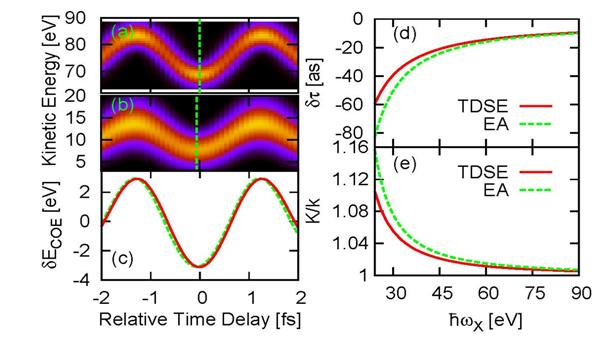
Fig. 1. Streaked photoemission from 1D model hydrogen atoms. TDSE calculations for XUV pulses with a central photon energy of (a) 90 eV and (b) 25 eV. (c) Corresponding center-of-energy shifts δE_COE(τ) for =90 eV (solid line) and 25~eV (dashed line). To facilitate the identification of the relative temporal shifts δτ, δE_COE(τ, =90 eV) is normalized to the =25 eV result. (d) δτ and (e) oscillation amplitude relative to the SFA for TDSE (full line) and eikonal approximation (dashed line) calculations.

Future plans: We intend to (i) continue to investigate the effect of interactions that are not included in SFA and (ii) examine the influence of initial-state polarization in the streaking IR-laser field on photoelectron spectra and time delays. We will seek contact with experimental groups to explore the feasibility of and ideal parameters for the observation of Coulomb-laser effects beyond the standard SFA in streaked photoemission spectra [4].

Collaborator: Chang-hua Zhang (KSU)

[1] C.-H. Zhang and U. Thumm, Phys. Rev. Lett. 102, 123601 (2009).

[2] C.-H. Zhang and U. Thumm, invited paper, XXVI ICPEAC, Kalamazoo, Journal of Physics: Conf. Series 194, 012055 (2009).

[3] C.-H. Zhang and U. Thumm, Phys. Rev. A 80, 032902 (2009).

[4] C.-H. Zhang and U. Thumm, Phys. Rev. A 82, 043405 (2010).

2.1.2 Streaking and Wigner time delays in photoemission from atoms

Project scope: To compare different measures for the time delay in photoemission from atoms by XUV photons and to examine Wigner and streaking time delays [1-6] for the photoionization of atoms [3,5].

Recent progress: Streaked photoemission metrology allows the observation of an apparent relative time delay between the detection of photoelectrons (Pes) from different initial electronic states [1-3,6,7]. Theoretically, photoemission delays can be defined based on (i) the phase shift the photoelectron wavefunction accumulates during the release and propagation of the PE (``Wigner delay") and, alternatively, (ii) the streaking trace in the calculated photoemission spectrum (``streaking delay") , while experimentally time delays can only be deduced from streaked PE spectra [1,3,6]. We investigated the relation between Wigner and streaking delays in the photoemission from atoms and solid surfaces. For surfaces and assuming a vanishing IR-skin depth, both Wigner and streaking delays can be interpreted as an average propagation time needed by photoelectrons to reach the surface, while the two delays differ for non-vanishing skin depths [3,4]. For atomic targets, the difference between Wigner and streaking delays depends on the range of the ionic potential [3].

Future plans: We intend to clarify the precise interpretation of and relations between different time-delay measures based on specific numerical examples for photoemission from atoms and surfaces.

Collaborator: Chang-hua Zhang (KSU)

[1] C.-H. Zhang and U. Thumm, Phys. Rev. Lett. 102, 123601 (2009).

[2] C.-H. Zhang and U. Thumm, invited paper, XXVI ICPEAC, Kalamazoo, Journal of Physics: Conf. Series 194, 012055 (2009).

[3] C.-H. Zhang and U. Thumm, Phys. Rev. A 84, 033401 (2011).

[4] C.-H. Zhang and U. Thumm, Phys. Rev. A, submitted; http://arxiv.org/abs/1102.0751

[5] C.-H. Zhang and U. Thumm, Phys. Rev. A 82, 043405 (2010).

[6] M. Schultze et al., Science 328, 1658 (2010).

[7] A. L. Cavalieri et al., Nature 449, 1029 (2007).

2.1.3 Attosecond time-resolved probing of instantaneous AC Stark shifts in helium atoms

Project scope: To model, calculate, and understand the excitation and ionization of atoms in an IR-laser field with sub-optical-cycle (T_IR ) time resolution.

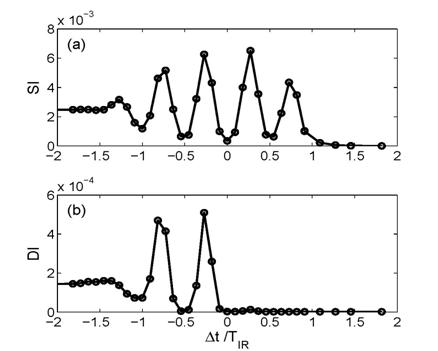
Recent progress: The role of laser-dressed highly excited energy levels in atomic excitation and ionization has been studied recently using attosecond technology [1,2]. We followed up on these studies and showed that this pump-probe technique also enables the measurement of instantaneous level shifts of bound atomic [3] (and molecular [4]) states in optical electric fields (Fig. 1). We demonstrated how the control of instantaneous level shifts can be exploited to gate strong-field phenomena, such as non-sequential double ionization (NSDI) [3] (Fig. 2).

Based on numerical solutions of TDSE for either one or two active electrons, we developed a method for observing time-dependent instantaneous level shifts in an oscillating strong IR field, using a single tunable XUV pulse to probe excited states of the perturbed atom. We assumed IR-laser fields with negligible distortion of the He ground state, which are, however, strong enough to couple low-lying excited and continuous states, inducing noticeable level splitting, shift, and decay. 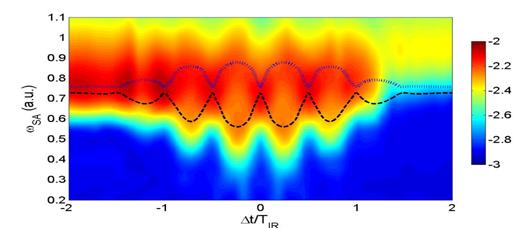We fixed the number of XUV cycles and varied the central frequency ω_SA of the XUV pulse (Fig. 1). Key to our investigation is the observation that, for a given ω_SA of the attosecond XUV pulse and depending on the delay ∆t between pump and probe pulse, the IR pulse may shift low-lying bound states into or out of resonance with one-photon excitations from the He ground state. The excited atom may then be easily ionized by the remaining IR pulse. Applying the SA pulse while instantaneous level energies are off (in) resonance with ω_SA, results in less (more) excitation and thus less (more) ionization out of excited states. This suggests that detection of the ionization probability as a function of ω_SA and ∆t can be used to experimentally track instantaneous Stark shifts [3,5].

Fig. 1. Ionization probabilities (logarithmic color scale) of He calculated in single-active-electron-approximation as a function of the center frequency ωSA of the (single) attosecond (SA) XUV pulse and time delay Δt between the SA and IR laser pulses in units of the IR laser period TIR. Superimposed dashed and dotted curves show the quasi-static energy differences between the Stark-shifted 1s and 2s (dashed line) and 1s and 2p (dotted line) levels.
	Fig. 2. Probabilities for single ionization (SI) (a) and double ionization (DI) (b) as a function of the time delay between SA and IR pulses. The SA pulse has a central frequency of 0:76 a.u. and a peak intensity of 2x10^13W/cm^2. The IR pulse has a central wavelength of 800 nm and a peak intensity of 3x10^14W/cm^2. The simulation results (circles) are interpolated by lines.

Future plans: The proposed method (i) allows the detection of instantaneous atomic energy gaps with sub-laser-cycle time resolution and (ii) can be applied as an ultrafast gate for more complex processes such as NSDI [3]. We intend to continue to search for ideal laser parameters and targets for the observation, with sub-IR-cycle resolution, of AC Stark shifts in delay-dependent single and double ionization probabilities. This may lead to new schemes for the coherent control of NSDI, high harmonic generation, and molecular dissociation, for which we hope to find suitable proof-of-principle examples.

Collaborators: Feng He (SJTU Shanghai, China), Camilo Ruiz (CLPU Salamanca, Spain), Andreas Becker (JILA, Boulder, CO)

[1] P. Johnsson et al., Phys.Rev. Lett. 99, 233001 (2007).

[2] P. Ranitovic et al., New J. Phys. 12, 013008 (2010).

[3] F. He, C. Ruiz, A. Becker, and U. Thumm, Phys. Rev. Lett, submitted; arxiv.org/abs/1105.5204

[4] F. He, A. Becker, and U. Thumm, Phys. Rev. Lett. 101, 213002 (2008).

[5] H. Wang, M. Chini, S. Chen, C.-H. Zhang, F. He, Y. Cheng, Y. Wu, U. Thumm, and Z. Chang, Phys. Rev. Lett. 105, 143002 (2010).

2.1.4 Electron interference in atomic photoionization by a single few-cycle IR laser pulse

Project scope: To model, calculate, and understand interference structures in photoelectron spectra, in particular, to distinguish structures that are due to above-thresholds ionization from intra-IR cycle electron interferences.

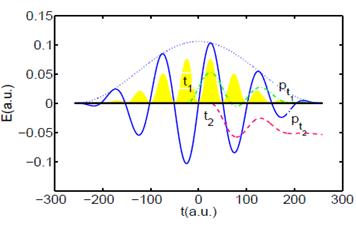
Recent progress: We analyzed recently measured [1] interference patterns in momentum-resolved single-ionization photoelectron spectra from He targets with regard to the interference of specific contributions to calculated photoelectron spectra that originate from a few selected sub-laser-cycle time intervals during the laser-atom interaction (Fig. 1). For contributions from just two such narrow time intervals that are centered at successive maxima of the laser-electric field with lengths of a few attoseconds, our calculations reproduce some of the measured interference structure in the momentum-resolved spectra. By selecting photoelectron wave packets that are released with inter- or intra-IR-cycle spacings [2], we were able to distinguish known above-threshold-ionization (ATI) interferences and non-ATI interference structures in simulated photoelectron spectra [3].

Fig. 1. IR-laser electric field (solid line) and field envelope (dotted line). The yellow/gray shaded area shows the photoelectron yields calculated in strong-field approximation (in arbitrary units). Also shown are two classical trajectories (dashed lines) for electrons that are emitted within an IR cycle, at times t1 and t2 and detected with momenta pt1 and pt2, respectively. The oscillation amplitudes of these trajectories are given in arbitrary units.

Future plans: We intend to provide a more complete interpretation of interferences in the momentum-resolved photoionization of atoms by single few-cycle IR pulses in terms of a semiclassical analysis of relevant electron trajectories.

Collaborator: Aihua Liu (KSU)

[1] R. Gopal et al., Phy. Rev. Lett. 103, 053001 (2009).

[2] D. G. Arbo et al., Phys. Rev. A 81, 021403(R) (2010).

[2] “Sub-optical-cycle photoelectron-wave-packet interference in few-cycle laser pulses”, A. Liu and U. Thumm, in preparation.

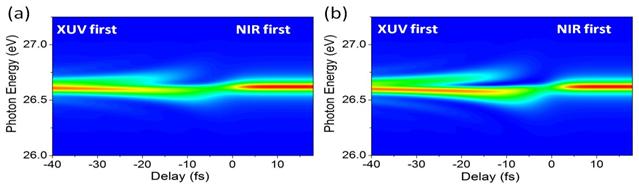
2.1.5 Time-resolved autoionization

Project scope: To simulate absorption spectra for the time-dependent autoionization from atoms.

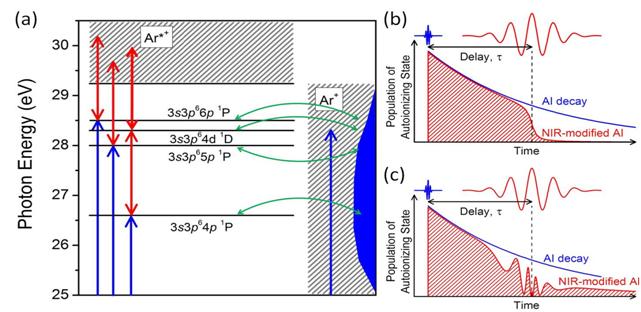
Recent progress: Autoionization in argon atoms was recently studied experimentally by transient absorption spectroscopy with isolated attosecond pulses [1] (Fig. 1). The peak position, intensity, line width, and shape of the 3s3p⁶np ¹P Fano resonance series (26.6-29.2 eV) were modified by intense few-cycle near infrared laser pulses, while the delay between the attosecond pulse and the laser pulse was changed by a few femtoseconds. Our numerical simulations [1] revealed that the experimentally observed splitting of the 3s3p⁶4p ¹P line is caused by the coupling between two short-lived highly-excited states in the strong laser field (Fig. 2).

Future plans: Our simulations [1] of the laser-induced coupling of the 3s3p⁶4p and 3s3p⁶4d autoionizing states were performed based on the heuristic interaction matrix elements [2]. In our model, the 3s3p⁶5p and 3s3p⁶6p states as well as the Ar^*+ (3s3p⁶εl) continuum are ignored, but coupling to the Ar⁺ (3s²3p⁵εl) continuum via configuration interaction is included. We plan to develop a fully ab-initio time-dependent calculation for He atoms and use this calculation to scrutinize our semi-heuristic calculation in Ref. [1].

Fig. 1. (a) Schematic representation of argon autoionizing states exposed to the strong laser field. The blue arrows indicate the attosecond XUV excitation of the ground state to the 3s3p⁶np ¹P states as well as to the Ar⁺ (3s²3p⁵εl) continuum. The red arrows indicate the NIR laser coupling between the autoionizing states and the Ar^*+ (3s3p⁶εl) continuum or to 3s3p⁶nl autoionizing states. The configuration interaction (green arrows) couples all autoionizing states to the Ar⁺ continuum. (b) Autoionization decay modified by NIR laser-induced coupling to the Ar^*+ (3s3p⁶εl) continuum. Ionization truncates the autoionization decay, resulting in a shorter lifetime and a broader, shifted resonance peak. (c) Autoionization decay modified by NIR laser-induced coupling to 3s3p⁶nl autoionizing states. Rabi oscillation between the two states results in AC Stark-like splitting.

Fig. 2. Simulated dipole radiation spectrum of laser-induced coupling of the 3s3p⁶4p and 3s3p⁶4d autoionizing states. The XUV laser has a pulse duration of 140 as and intensity of 10¹⁰ W/cm². The NIR laser had a pulse duration of 8 fs and intensity of (a) 5×10¹¹ W/cm² and (b) 1×10¹² W/cm².

Collaborators: Authors of ref. [1] (KSU and University of Central Florida, Orlando)

[1] H. Wang, M. Chini, S. Chen, C.-H. Zhang, F. He, Y. Cheng, Y. Wu, U. Thumm, and Z. Chang, Phys. Rev. Lett. 105, 143002 (2010).

[2] C.-H. Zhang and U. Thumm, Phys. Rev. A 80, 032902 (2009).

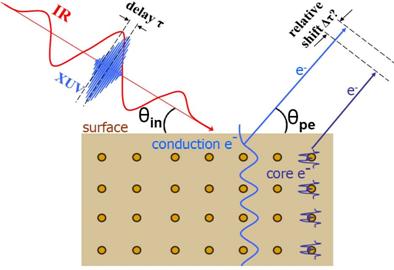
2.2 Time-resolved electronic dynamics in complex systems

2.2.1 Attosecond time-resolved photoelectron spectroscopy of metal surfaces

Project scope: To model the time-resolved photoelectron (PE) emission in pump-probe and streaking experiments with complex targets.

Recent progress: In attosecond time-resolved PE streaking experiments on metal surfaces, attosecond extreme ultraviolet (XUV) light pulse are used to release electrons from either bound core levels or delocalized conduction-band states (Fig. 1). The released electrons get exposed to (“streaked by”) the same IR probe pulse, that was also used to generate the XUV pulse via harmonic generation. The two laser pulses are thus synchronized with a precisely adjustable time delay τ, and the measured asymptotic PE kinetic energy E depends on τ. By varying τ, the time-resolved PE kinetic energy distribution P(E,τ) can be recorded. This method was first successfully applied to isolated atoms in the gas phase [1] and, more recently, to tungsten [2] and platinum [3] surfaces. By using attosecond streaking spectroscopy, Cavalieri et al. [2] measured a relative delay of 110 ± 70 as between the detection of electrons that are photoemitted by absorption of a single XUV photon from 4f-core and conduction-band levels. Due to their different initial energies, PEs from core and conduction-band levels can be easily separated in the energy-differential spectra.

Fig. 1. Attosecond streaking spectroscopy at metal surfaces. Delocalized conduction electrons and localized core-level electrons are released by an attosecond XUV pulse (photoelectric effect) and streaked by an IR laser pulse. By changing the delay between the two pulses, the delay between the detection of photoelectrons that originate in conduction band and core levels can be measured.

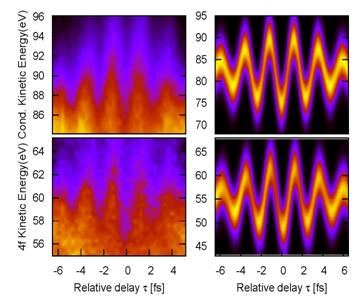
For the W (110) surface we use measured values for the work function (W=5.5 eV), Fermi energy (E_F = 4.5 eV), and lattice constant in direction perpendicular to the surface (a = 3.13 Å). We calculated the energy-resolved spectra P_CB (E, τ) and P_4f (E, τ) for the two groups of PEs as a function of τ [4,5]. The comparison of experiment and theory in Fig. 2 shows that our IR pulse modulation of the PE kinetic energy agrees with the experiment. In order to find the temporal shift between the two calculated spectra in the right column of Fig. 2, we calculated their center-of-energies E_COE (τ). The temporal shift between 4f core-level and conduction-band electrons is recognizable in Fig. 3 for both experimental data and calculation.

		Fig. 2. Time-resolved photoelectron spectra for emission out of the conduction band (top) and 4f core level (bottom) of a W (110) surface, as a function of the delay between the XUV and IR pulses. Experimental results [2] (left) in comparison with our calculation [4] (right).
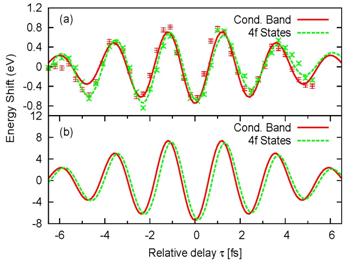
	Fig. 3. Streaked electron spectra for photoemission from conduction-band and 4f core levels of a W (110) surface. Center-of-energy shift as a function of the delay between the XUV and IR pulse. (a) Experimental results from [2]. The damped sinusoidal curves are fits to the raw experimental data (points with error bars). (b) Calculated results showing a relative shift of 110 as between the two groups of electrons. For better comparison, energies for the 4f photo-electrons are multiplied by a factor 2.5 in (a) and 1.1 in (b).

Future plans: We intend to refine our calculations in [4] by including diffraction effects during the propagation of PEs inside the solid and by allowing for arbitrary angles of IR-light/X-ray incidence and PE emission: (i) Since the transport (in our model the electron mean-free path λ) depends on the PE kinetic energy, and thus the XUV frequency ω_X, we anticipate future tests of this predicted sideband enhancement effect in experiments with tunable ω_X. (ii) While we believe fully localized states are a good approximation for the 4f state in tungsten [4,5], the fully delocalized plane wave (jellium) approximation [6] does not take into account that 5d6s conduction-band states in tungsten have some localized character as well. For a fixed value of λ=5 a.u., allowing for partial localization of the conduction-band states is expected to decrease the temporal shift between core and conduction-band levels. In an improved model, this decrease could be compensated by increasing λ to a value closer to accepted values for tungsten [5,7]. We thus plan to improve our modeling of the metal conduction band and the propagation of photoelectrons inside the solid.

Collaborator: Chang-hua Zhang (KSU)

[1] M. Hentschel et al., Nature 414, 509 (2001); R. Kienberger et al., Nature 427, 817 (2004).

[2] A. L. Cavalieri et al., Nature 449, 1029 (2007).

[3] L. Miaja-Avila et al., Phys. Rev. Lett. 101, 046101 (2008).

[4] C.-H. Zhang and U. Thumm, Phys. Rev. Lett. 102, 123601 (2009).

[5] C.-H. Zhang and U. Thumm, invited paper, XXVI ICPEAC, Kalamazoo, Journal of Physics: Conf. Series 194, 012055 (2009).

[6] A. Schmitz, J. Shaw, H. S. Chakraborty, and U. Thumm, Phys. Rev. A 81, 042901 (2010).

[7] C.-H. Zhang and U. Thumm, Phys. Rev. A 80, 032902 (2009).

2.2.2 Laser-assisted photoemission from adsorbate-covered metal surfaces:

Time-resolved core-hole relaxation dynamics from sideband profiles

Project scope: We attempt to model the time-resolved photoelectron (PE) emission and Auger decay in pump-probe experiments with adsorbate-covered surfaces and thin films.

Fig.1. Sketch of the emission of substrate (core level and conduction band) and adsorbate (core level and Auger) electrons by an XUV pulse. Photoreleased electrons are exposed to a weak delayed IR pulse.

Recent progress: Illumination of an adsorbate-covered metal surface with an XUV pulse and a delayed IR laser pulse (Fig. 1) can result in sidebands in the PE spectra [1]. We developed a theoretical model for the delay-dependent photoemission process and showed how the relaxation dynamics of XUV-induced core-level holes in adsorbate atoms can be deduced from the temporal shift between sideband peaks in the spectra of secondary adsorbate (Auger) electrons and conduction band (CB) PEs from the substrate (Fig. 2) [2-4].

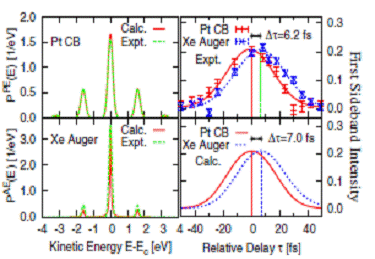
Fig. 2. Theoretical [4] and experimental [1] PE spectra for laser-assisted photoemission from a Xe/Pt(111) surface. Left: Sideband intensities for no delay (τ=0) between XUV and IR pulses for XUV-emitted conduction-band electrons (Pt CB) from the Fermi level (top) and Xe Auger electrons (bottom). Right: Experimental (top) and calculated (bottom) first sideband intensities for Pt CB electrons and Xe Auger electrons, revealing a temporal shift Δτ. Sideband intensities in the AE spectra are multiplied by a factor of 2.16.

In comparison with gaseous targets, we found a characteristic sideband-intensity enhancement in the laser-assisted photoemission from the substrate core-levels [3,4]. This effect can be tested in experiments with tunable XUV wavelength. Our calculated PE spectra support first time-resolved experiments for Xe-covered Pt(111) surfaces, enabling the direct analysis in the time domain of surface dynamical processes. This intensity redistribution between the main and sideband peaks in core level photoelectron spectra from metals surfaces is related to the transport of photoreleased electrons in the substrate [2,4].

Future plans: We intend to systematically apply quantum mechanical S-matrix theory to the study of time-resolved core-hole relaxation spectroscopy on adsorbate-covered surfaces.

Collaborator: Chang-hua Zhang (KSU)

[1] L. Miaja et al., Phys. Rev. Lett. 101, 046101 (2008).

[2] C.-H. Zhang and U. Thumm, Phys. Rev. Lett. 102, 123601 (2009).

[3] C.-H. Zhang and U. Thumm, invited paper, XXVI ICPEAC, Kalamazoo, Journal of Physics: Conf. Series 194, 012055 (2009).

[4] C.-H. Zhang and U. Thumm, Phys. Rev. A 80, 032902 (2009).

2.2.3 Dynamical image-charge effects in streaked photoelectron spectra of metal surfaces

Project scope: To provide theoretical guidance towards the application of time-resolved streaked photoelectron spectroscopy for the investigation of ultrafast plasmonic dynamics in complex targets, such as clusters, carbon nanotubes, and surfaces.

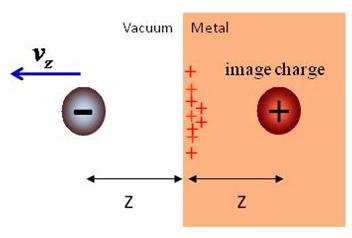
Fig. 1. A moving photoelectron excites surface and bulk plasmons in the metal substrate that lead to a dynamical redistribution of surface charge. This charge redistribution, in turn, acts back on the photoelectron and changes the photoemission time delay. In the limit where the photoelectron is far away from the surface and at rest, the net effect of the charge redistribution amounts to the interaction between the photoelectron and its fictitious image charge.

Recent progress: The release of conduction-band electrons from a metal surface by a sub-femtosecond XUV pulse, and their propagation through and near the solid [1,2,3,4], provokes a dielectric response in the solid that acts back on the photoelectron (PE) wave packet (Fig. 1). We modeled the response of the metal due to excitation of bulk and surface plasmons induced by the creation and propagation of PEs in the solid in terms of an effective potential that depends on the velocity of the PE. We numerically calculated the (wake) potential associated with this PE self-interaction and showed that it induces a considerable XUV-frequency-dependent temporal shift in streaked-photoemission spectra [5], suggesting the observation of the ultrafast solid-state dielectric response in contemporary streaked photoemission experiments [4]. We are currently analyzing the dependence of this relative shift on the XUV frequency as well as on solid-state characteristics, such as the bulk-plasmon frequency, the IR-skin depth, and the PE transport in the solid (Fig. 2).

Future plans: We plan to (i) further improve our modeling of the transport (including diffraction effects) of released PEs inside the substrate and (ii) collaborate with experimental groups to explore the feasibility of and ideal parameters for the observation of plasmon response effects ( i.e., the time-resolved creation of “image charges”) during and after the XUV-pulse-triggered release of PEs from metal surfaces [4,5].

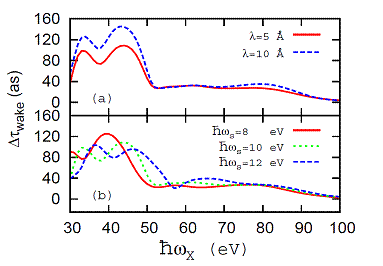
Fig. 2. Contribution Δτwake to the streaking delay in photoemission from a metal surface due to the dynamic plasmon response. The relative delay Δτwake is shown as a function of the XUV frequency ωX for vanishing IR skin depth and at different (a) photoelectron mean-free paths λ and (b) surface-plasmon frequencies ωS. We obtained Δτwake as the difference of time delays in calculated streaked photoemission spectra that included either the dynamical plasmon response or just the static image potential.

Collaborator: Chang-hua Zhang (KSU)

[1] C.-H. Zhang and U. Thumm, Phys. Rev. Lett. 102, 123601 (2009).

[2] C.-H. Zhang and U. Thumm, invited paper, XXVI ICPEAC, Kalamazoo, Journal of Physics: Conf. Series 194, 012055 (2009).

[3] C.-H. Zhang and U. Thumm, Phys. Rev. A 80, 032902 (2009).

[4] A. L. Cavalieri et al., Nature 449, 1029 (2007).

[5] “Probing dielectric response effects with attosecond time-resolved streaked photoelectron spectroscopy of metal surfaces”, C.-H. Zhang and U. Thumm, Phys. Rev. A., submitted; http://arxiv.org/abs/1102.0751

2.3 Electronic structure of flat and vicinal surfaces

Project scope: (i) To develop models for the efficient representation of the valence electronic structure of complex systems in terms of single-electron effective potentials and (ii) to use these effective potentials in modeling the interaction of particles and (XUV and IR) radiation with metal surfaces and carbon nanotubes.

Recent progress: We developed a new set of computer programs to calculate the ground-state electronic structure of arbitrarily shaped metallic surfaces and tested our codes in applications to flat and vicinal metal and semi-conductor surfaces [1,2]. We used a density functional model for the ground-state electronic structure of the surface that included linear and quadratic electronic response terms and heuristic core potentials centered at the lattice points, in order to provide realistic, self-consistent surface potentials and corresponding electronic charge densities (Fig. 1). We employed these potentials to model the charge-transfer dynamics during ion-surface collisions, based on a Newns-Anderson approach and including image-charge interactions and electron translation factors [3,4].

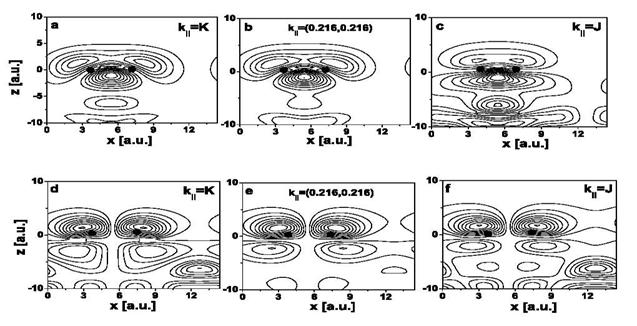
Fig. 1. Charge densities of (a)–(c) π bonding and (d)–(f) π* anti-bonding surface states on the (2 × 1)-reconstructed Si (100) surface. The first 4.5 layers are shown. The parallel Bloch momentum k_|| changes along a straight-line connecting the high-symmetry end points K and J in the surface Brillouin zone. The positions of the Si cores forming the surface dimer are indicated by dots [4].

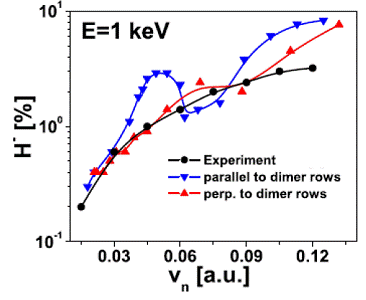
Fig. 2. Negative-ion survival as a function of the exit velocity component normal to the surface for incident 1 keV hydrogen anions that are reflected on a (2×1)-reconstructed Si(100) surface. The angles of incidence (relative to the surface plane) are between 3^0 and 25^0. Upward pointing triangles give final anion yields for projectiles moving perpendicularly to Si-dimer rows. Inverted triangles correspond to trajectories oriented parallel to dimer rows. Circles show the measured [5] negative-ion yields on Si surfaces.

Employing these effective potentials, we calculated the yield of outgoing negative hydrogen ions after scattering off a reconstructed Si (100) surface [3,4]. We find that the outgoing H^- fraction is mainly determined by electron capture from dangling-bond surface-state resonances at relatively large distances from the surface. Our results are in fair agreement with the experimental results of Maazouz et al. [5] and with recent independent calculations by Garcia et al. [6] (Fig. 2).

Future plans: We will test our numerical implementation of this method first by comparing workfunctions for flat surfaces and work function changes due to vicinal superstructures with published data. We intend to investigate resonance formation, charge exchange, and time-resolved photoemission near vicinal and other nano-structured surfaces. In particular, we plan to assess the importance of lateral confinement effects [7] (evidence of which was found in photoemission experiments) on ion neutralization and photoemission.

Collaborator: Boyan Obreshkov (KSU)

[1] B. Obreshkov and U. Thumm, Phys. Rev. A 74, 012901 (2006).

[2] B. Obreshkov and U. Thumm, Surf. Sci. 601, 622 (2007).

[3] B. Obreshkov and U. Thumm, Phys. Rev. A 76, 052902 (2007).

[4] B. Obreshkov and U. Thumm, Phys. Rev. A 83, 062902 (2011).

[5] M. Maazouz et al., Surf. Sci. 398, 49 (1998).

[6] E. A. Garcia et al., Surf. Sci. 600, 2195 (2006).

[7] U. Thumm, P. Kürpick, and U. Wille, Phys. Rev. A 61, 3067 (2000).

2.4 Image-potential states of single- and multi-walled carbon nanotubes

Project scope: (i) To develop models for the efficient representation of the valence electronic structure of carbon nanotubes (CNT) in terms of single-electron effective potentials and (ii) to use these potential for the investigation of two-photon photoemission processes.

Recent progress: We have investigated the formation of image-potential states near the surfaces of single- and multi-walled CNT (Fig. 1). These states are confined between the self-induced image potential on the vacuum side and the surface barrier. We calculated binding energies and wave functions by modeling the interactions inside the nanotube with a cylindrical jellium-like short-range potential that is parameterized to ensure the correct vacuum to surface transition.

We found an interesting variation of the image-state properties on the nanotube diameter [1], which is due to the difference in the radial dependence of the induced image potential and the centrifugal potential. Our results predicting the existence of image-potential states in CNTs were confirmed in recent time-resolved photoemission experiments [2].

Fig. 1. Visualization of an image electron wave function for a multi-walled carbon nanotube.

Future plans: Image states are sensitive probes of the dielectric response of CNTs. Their properties are affected by the anisotropic polarizability of the tube. A realistic description of electronic image-state spectra thus requires detailed knowledge of the anisotropic dynamic susceptibility of CNTs as a function of momentum, length, and the tube primitive indices. We intend to improve our perfect-cylindrical-conductor simulation [1] by calculating the anisotropic dielectric tensor within a tight-binding approach, providing accurate binding energies and lifetimes.

Collaborators: Himadri S. Chakraborty (NW Missouri State University, Maryville)

[1] M. Zamkov, H.S. Chakraborty, A. Habib, N. Woody, U. Thumm, and P. Richard, Phys. Rev. B 70, 115419 (2004).

[2] M. Zamkov, N. Woody, B. Shan, H.S. Chakraborty, Z. Chang, U. Thumm, and P. Richard, Phys. Rev. Lett. 93, 156803 (2004).

3. Laser-assisted collisions

Project scope: To investigate the effects a strong laser field has on electron capture, emission, and level hybridization in ion-atom and particle-surface interactions. These investigations are also intended to assist in the planning of future experiments with crossed laser and pulsed particle beams.

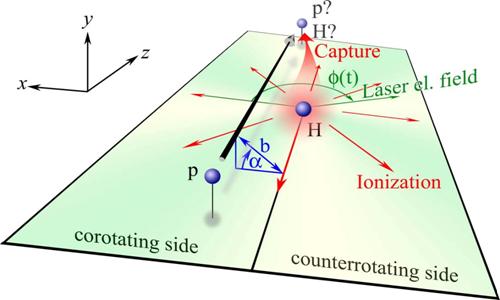
Fig. 1. Collision scenario for a proton colliding at impact parameter b with an atomic hydrogen target. For positive impact parameters, the projectile follows the rotating circularly polarized laser field (“co-rotating” case). For negative impact parameters, the projectile moves against the rotating electric field (“counter-rotating” case). α denotes the angle between the collision plane and the plane defined by the rotating laser electric field vector.

Recent progress: We calculated cross sections for electron capture and emission in slow (keV) prototype proton-hydrogen collisions in the presence of a strong 1064 nm laser field. We first developed and applied a simplified 2D reduced dimensionality model of the scattering system [1] in which the motion of the active electron and the laser electric field vector are confined to the scattering plane (Fig. 1). We then extended these 2D calculations by propagating the full time-dependent 3D Schrödinger equation on a numerical grid [2]. We examined the probabilities for electron capture and ionization as a function of the laser intensity, the projectile impact parameter b, the angle α between the collision plane, the plane in which the circularly polarized laser electric field vector rotates, and the laser phase φ that determines the orientation of the laser electric field with respect to the internuclear axis at the time of closest approach between target and projectile. Since the laser electric field breaks the cylindrical symmetry of the collision system, our 3D calculations of laser-assisted capture and ionization cross sections require the inclusion of a large number of projectile trajectories. We found a relatively weak variation of the laser-phase-resolved capture cross section on the angle α, such that our 2D and full 3D cross sections are qualitatively similar functions of φ.

We tested the accuracy of our 3D numerical wave function propagation calculation by turning the laser field off and found agreement with known experimental capture cross sections for p + H collisions. Both, laser-assisted ionization and capture probabilities show a strong dependence on φ and on the helicity of the circularly polarized laser light (Fig. 2). For intensities above 2x10¹² W/cm², we predict a noticeable circular dichroism in the capture probability for slow proton-hydrogen collisions that persist after averaging over φ. Capture and electron emission probabilities defer significantly from results for laser-unassisted collisions. Ionization probabilities depend less sensitively on φ, and their phase averages differ much less for co- and counter-rotating collisions than the phase-averaged capture probabilities. For 1.21 keV protons, the difference in the capture cross sections for co- and counter rotating collisions at a laser intensity of 5x10¹³ W/cm² amounts to 40% in our 2D and to 15% in our 3D calculations. Our full 3D calculations confirm evidence found in previous 2D calculations for a charge-resonance-enhanced-ionization mechanism that may enable the measurement of φ. We predicted that laser pulses with lengths of a few nanoseconds and intensities of about 10¹² W/cm² and higher would allow for the experimental verification of the calculated dichroism in the capture probability.

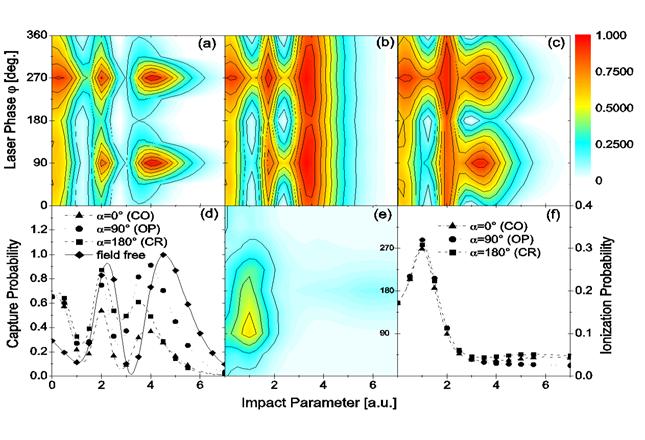
Fig. 2. (a) - (c) Contour plots of the electron capture probability and (e) the ionization probability as a function of impact parameter and laser phase φ for (a, e) co-rotating (CO), (b) off-plane with α = ± 90 degrees (OP), and (c) counter-rotating (CR) collisions. Also shown are the phase-averaged results for (d) capture and (f) ionization, together with the field-free probabilities.

Future plans: …are largely dependent on the experimental progress in synchronizing particle beams with intense laser pulses. If encouraged by future experiments, we will attempt to refine our studies, e.g., by including electronic correlation in two-electron projectile ions, by providing sublevel-specific excitation and angle-resolved electron-emission cross sections, and by adjusting collision and laser parameters to the experiment.

Collaborator: Thomas Niederhausen (KSU, now at University of Madrid, Spain)

[1] T. Niederhausen, B. Feuerstein, and U. Thumm, Phys. Rev. A 70, 023408 (2004).

[2] T. Niederhausen and U. Thumm, Phys. Rev. A 73, 041404(R) (2006).

4. Highly correlated negative-ion resonances in photodetachment and electron scattering processes

Project scope: (i) To explore the effect of electronic correlation in negative ions on photo-detachments and electron-scattering processes and (ii) to provide basic data (e.g., scattering lengths) for the modeling of ultracold collisions between alkali atoms and the formation of alkali dimers in atomic traps.

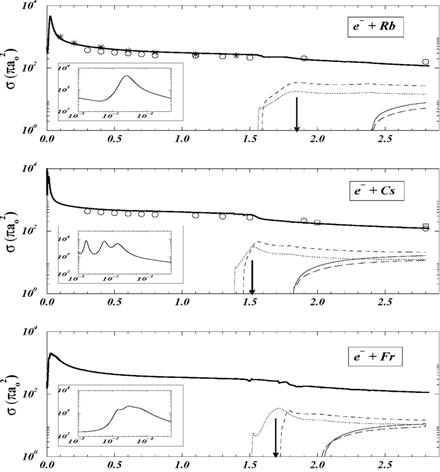
Recent progress: In the field of electron‑atom interactions, alkali‑metal atoms and noble gases are frequently chosen targets for detailed experimental and theoretical studies, owing both to their relative theoretical simplicity and to the relative ease with which they can be handled experimentally. The heavier targets, like rubidium, cesium, or francium allow for the exploration of relativistic effects, which are too small to be easily observed in lighter atoms.

For the electron‑cesium system, two multiplets of narrow shape resonances (with widths of a few meV) are of particular interest. We have shown [1] that these resonances are influenced by both (two‑electron) core-polarization and relativistic effects. The former convert the ³P^o_J negative-ion states from bound states to resonances. The latter add fine‑structure splitting and finite auto-ionization widths to ³P^e_J states that in LS coupling are strictly uncoupled to the adjacent continuum (Fig. 1). Our calculations predict the same resonances to occur in Rb^‑ and Fr^‑ [2].

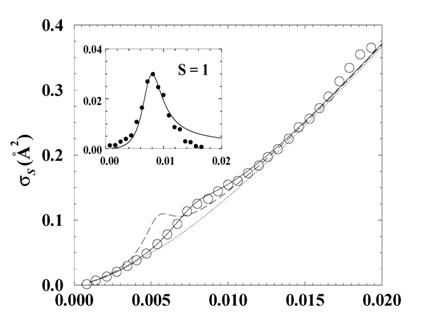
We have identified and characterized a large number of scattering resonances in elastic, inelastic, angle-differential, and total electron-scattering cross sections for Rb, Cs, and Fr (atomic) targets. Our results for ³P^o and ³F^o shape resonances and ³P^e, ¹P^o, and ¹D⁰ Feshbach resonances of Rb^-, Cs^-, and Fr^- negative ions are in agreement with available experimental data [2]. We have calculated the ³S^e and ¹S^e scattering lengths in ultraslow collisions of electrons with ground state Rb, Cs, and Fr atoms. These calculations are based on a new relativistic effective-range theory that allows us to extrapolate eigenphases that are provided by relativistic Dirac R-matrix calculations to zero energy [6]. Recently, our scattering lengths have contributed to the prediction of a new class of highly excited, trilobite-shaped states of Rb₂ dimers [7].

E(eV)

Fig. 1. Total elastic (thick solid line) and inelastic cross sections: ns1/2 → np1/2 (dotted line), ns1/2 → np3/2 (short dashed line), ns1/2 → (n-1)d3/2 (long dashed line) and ns1/2 → (n-1)d5/2 (thin solid line) for e^-+ Rb, Cs, and Fr scattering (n = 5 for Rb, 6 for Cs, and 7 for Fr). The stars show the two-state close-coupling results of Fabrikant [3], the circles and squares represent the measured total scattering cross sections of Visconti et al. [4] and of Jaduszliwer and Chan [5]. For both experiments, the size of the symbols indicates the total error in the cross sections. The arrows point to the position of a ^3F^oresonance. The insets give the elastic cross section for energies below 0.5 eV and show the profile of the ^3P^o shape resonances.

E(eV)

Fig. 2. Angle-integrated photodetachment cross sections of Cs^- near the detachment threshold. Dotted curve: S=0 contribution only; dashed curve: total cross section for a cutoff parameter in the induced dipole potential rc = 2.1271; solid curve: same result for rc=2.1294. Circles show the experimental data of [8]. The inset shows our calculated S = 1 contribution to the detachment cross section (thick solid curve) compared to the background- subtracted measurement (dots) [8]. The sizes of the circles and dots indicate the experimental error.

Future plans: The dipole allowed J=1 term of the aforementioned ³P^o_J resonances was confirmed in measured photoelectron spectra [8] (Fig. 2). We plan to extend our relativistic calculations towards the consistent description of photo-processes within the Dirac R-Matrix approach [9]. These calculations will provide reliable absolute cross sections for the photodetachment of atoms and ions, as well as atomic alignment and coherence parameters.

We intend to study the decay and photodetachment of alkali-metal negative ions in the presence of strong external fields. Placing atoms or ions in a combination of laser and static fields allows the manipulation of the detachment process and to observe basic quantum mechanical effects such as multi-path interference. Reflection of the detached electron wave packet from the potential barrier created by a static external field leads to interference with the "direct" (downfield) emission path. Observation of these interferences provides detailed information about the electron-atom scattering amplitude at laser resolution. This project will build on our experience with Dirac R-matrix applications and will lead to a new set of computer programs to investigate photo-processes of stable or resonant, non-Coulombic systems with two active electrons in an external field. The provided basic atomic data are relevant for applications in chemistry, physics, and engineering.

Collaborators: Cristian Bahrim (Lamar University, Texas) and Ilya Fabrikant (University of Nebraska, Lincoln)

[1] U. Thumm and D.W. Norcross, Phys. Rev. Lett. 67, 3495 (1991); C. Bahrim and U. Thumm, Phys. Rev. A 61, 022722 (2000).

[2] C. Bahrim, U. Thumm, and I.I. Fabrikant, Phys. Rev. A 63, 042710 (2001); C. Bahrim and U. Thumm, Phys. Rev. A 64, 022716 (2001).

[3] I. Fabrikant, Phys. Lett. A 58, 21 (1976).

[4] P.J. Visconti, J.A. Slevin, and K. Rubin, Phys. Rev. A 3, 1310 (1971).

[5] B. Jaduszliwer and Y.C. Chan, Phys. Rev. A 45, 197 (1992).

[6] C. Bahrim, U. Thumm, and I.I. Fabrikant, J. Phys. B 34, L195 (2001).

[7] C. H. Greene, A. S. Dickenson, and H. R. Sadeghpour, Phys. Rev. Lett. 85, 2458 (2000).

[8] M. Scheer et al., Phys. Rev. Lett. 80, 684 (1998).

[9] C. Bahrim, I. I. Fabrikant, and U. Thumm, Phys. Rev. Lett. 87, 123003 (2001); C. Bahrim, I. I. Fabrikant, and U. Thumm, Phys. Rev. A 68, 063405 (2003).

Updated 9/28/11