 three-e
three-e
Visualization of Electron Correlations in Atoms
You have been calculating many-particle wavefunctions all the time,
but have you ever really seen one?
What is the issue?
The particles in a many-body system are not moving
independently of each other. Quantum mechanics provides us methods to calculate many-body wavefunctions. But have you ever seen one?
Where is the difficulty?
Visualization can be displayed only on a two-dimensional
surface while the spatial distribution of an N-electron atom is described by a
function of 3N variables. The key challenge in the visualization
is to identify the most
proper coordinates where the partial display of the wavefunctions can reveal the major
features of a physical state. We hope to see the face
of a physical state and find out if some of them are related so they can be named!

Visualization of singly excited states
The wavefunctions of the outermost electron for singly excited states of atoms are similar
to the hydrogenic wavefunctions which are easily found in textbooks. However,
when the outer electron is close to the inner ones, the electrons are indistinguishable
. This imposes symmetry conditions on the wavefunctions. To see Pauli correlation,
look at this link to see
the 1s2s 1Se, 1s2s 3Se,
1s2s 1Se and 3Se states of the helium
atom. You also will learn how to see the many-electron
wavefunctions there and learn what is Pauli correlation.

Visualization of doubly excited states
The prototypes are the doubly excited states of a helium atom.
The two electrons in doubly excited states move together and
they perform motions very similar to the vibration and rotation of a linear
triatomic molecule. To see that this is indeed the
case, we use the following example.
Consider the following five doubly excited states which are designated as 3s2 1S, 3s3p 3P, 3p2 1D, 3p3d 3F and 3d2 1G states in the conventional independent particle model.
One knows that this model is not quite right and you have to perform
configuration mixing calculation to obtain more accurate wavefunctions. You
then tabulate the results like this one
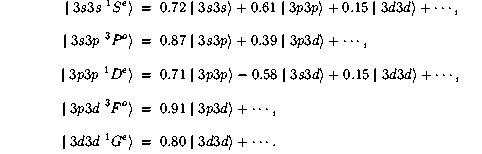
From these coefficients you wouldn't have expected that these states have anything in common. However, these states have the same faces, i.e.,
similar correlation patterns, if we plot these wavefunctions in appropriate coordinates. The pictures below show the density plots of the
wavefunctions.
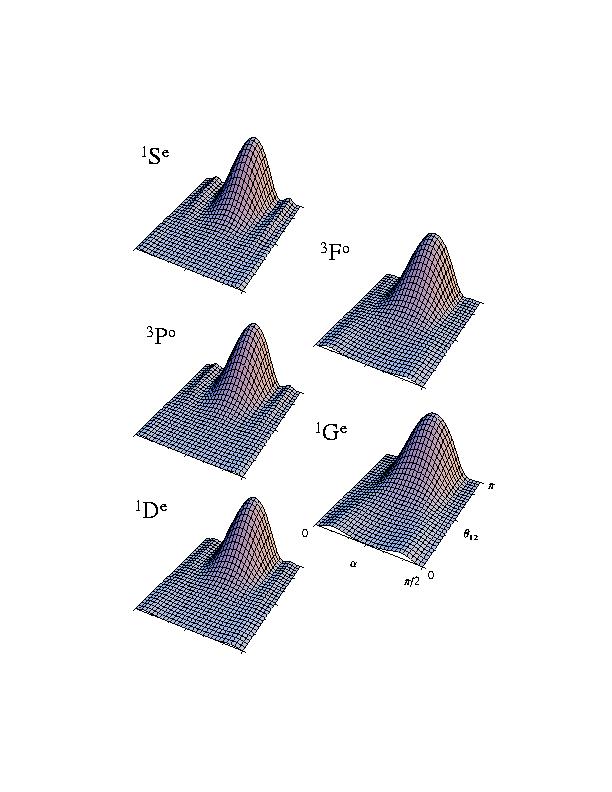
What we have plotted here are the densities. The two angles measure the relative
distances of the two electrons from the nucleus, and the angle between the two
electrons with respect to the nucleus, respectively. These plots show that the two
electrons and the nucleus have the shape of a linear triatomic molecule.
The two electrons stay at about the same distances from the nucleus and on opposite sides of the nucleus. Other doubly excited states have different
shapes or correlation patterns. Examination of the internal structure of the many-body
systems allow us to obtain classification schemes of the quantum systems.
This example shows how one can visualize the correlated motion of the two electrons in doubly excited states. Other doubly excited states have different correlation patterns
or different shapes. A more complete discussion of the classification of doubly excited states can be found in this review article

Electron Correlations in Triply Excited States

This project has been carried out mainly by
Toru Morishita who is now teaching at University of Electrocommunications in Tokyo.
Our recent effort has been directed at the visualization of correlations of the three electrons in triply excited states
. In other words, we want to know in what ways the three electrons are moving together in specific states. There are nine spatial coordinates for the description of the positions of the three electrons, and we hope to be able to make some sense by displaying these functions on a two-dimensional space!
We consider a special class of triply excited states-- the intrashell triply excited states where all the three electrons are at about the same distances from the nucleus. We fix the three distances and then we average over the whole rotational motion such that we are left with three degrees of freedom. In this limit we are considering the three electrons on the surface of a sphere and we ask what are the possible bending vibrational modes of the three electrons.
Clearly the most stable geometry for the three electrons is
a coplanar equilateral triangle where the three electrons lie on
the equator with the nucleus at the center. However, not all the states
can have this geometry. A quantum state is an eigenstate of total orbital
angular momentum, total spin angular momentum and the parity. Furthermore,
the wavefunctions are invariant under the exchange of any two electrons. These
symmetry conditions impose constraints on the wavefunctions.
We have identified three basic normal modes or shapes of the correlated motions of the three electrons:
(a) The three electrons form a coplanar equilateral triangle as in a planar BF3 molecule;
(b) The three electrons form an equilateral triangle but not coplanar. The wavefunction vanishes when the plane coincides with the nucleus; This is like a NH3 molecule.
(c) The three electrons can be coplanar but the equilateral triangular shape is not allowed. No known ground state molecules of this type exists.
The above qualitative conclusions are drawn from the plots of the
charge densities in suitable coordinate systems.

How to visualize the correlated motion of the three electrons?
There are nine spatial coordinates for the three electrons beside the spin functions. To display the nine-dimensional wavefunction is nearly impossible. Thus we
need to find out the essential variables. First we go to the body-frame of the atom
and average over the rotation of the whole atom. This leaves us with six coordinates. We then focus on intrashell states where the three electrons are set at the same distance from the nucleus. This leaves us with three coordinates remaining. We need to choose the three coordinates such that they exhibit the collective motion of the three electrons.
Now think that we have three electrons on the surface of a sphere where all the three electrons can roam around. The three electrons form a triangle which is the
 plane. The nucleus which is at the center of the sphere can lie on this plane. In this case we say the three electrons are coplanar with the nucleus. When it is away from the center, this plane makes an an angle
plane. The nucleus which is at the center of the sphere can lie on this plane. In this case we say the three electrons are coplanar with the nucleus. When it is away from the center, this plane makes an an angle  which is like the latitude on the surface of earth. We further need two angles
which is like the latitude on the surface of earth. We further need two angles
 and
and  to describe the shape of the triangle. These angles are shown here:
to describe the shape of the triangle. These angles are shown here:
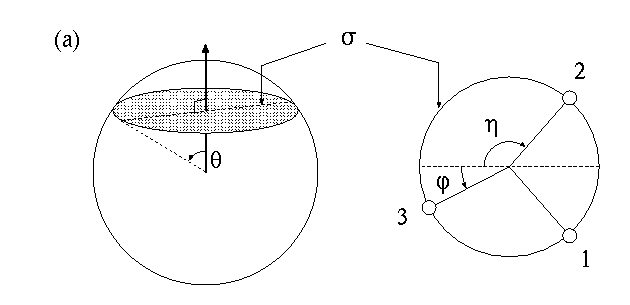
Our next task is to express the electron densities which are functions of the three angles above on a two dimensional surface. For this purpose,
we employ the equi-density surface plots. In frames below we display the surface where the density is 60% of the maximum which occurs inside at the center. The surface will be smaller if we plot, say 80%, of the maximum.

Visualization of 2l2l'2l" triply excited states
After these introductions we are ready to explain what we have plotted below. We will
illustrate the correlation patterns of the eight states of Li which are designated as 2s2 2p 2P0, 2s2p2 4Pe , 2s2p2 2Pe, 2s2p2 2De, 2s2p2 2Se, 2p3 4S0, 2p3 2P0, 2p3 2D0 in the conventional independent particle picture. The figures below display the geometry of the three electrons; they form three distinct groups:
One more remark is needed. The top left frame defines the three angles, but we only
show the middle triangle in the rest of the graphs. This triangle lies on the
equatorial plane and each point in this triangle represents a definite shape of the
triangle
(how confusing!) formed by the three electrons. The center where all the three diagonals
intersect represents an equilateral triangle. A point along any of the diagonal
represents an isoceles triangle formed by the three electrons. This is complicated, but
we are talking about the geometry of three electrons at the same time, not the simple
stuff of the position of each individual electrons. We have reduced the nine-dimensional
beast to three dimensions, and the waiting is almost over. Thanks for your patience!
Now we are ready to see the three-electron wavefunctions for the
first time! People have been calculating them for years but now they emerge from
the closet!
Here are their real faces. Now they are not just a set of digitized
numbers, they have features like you and me!
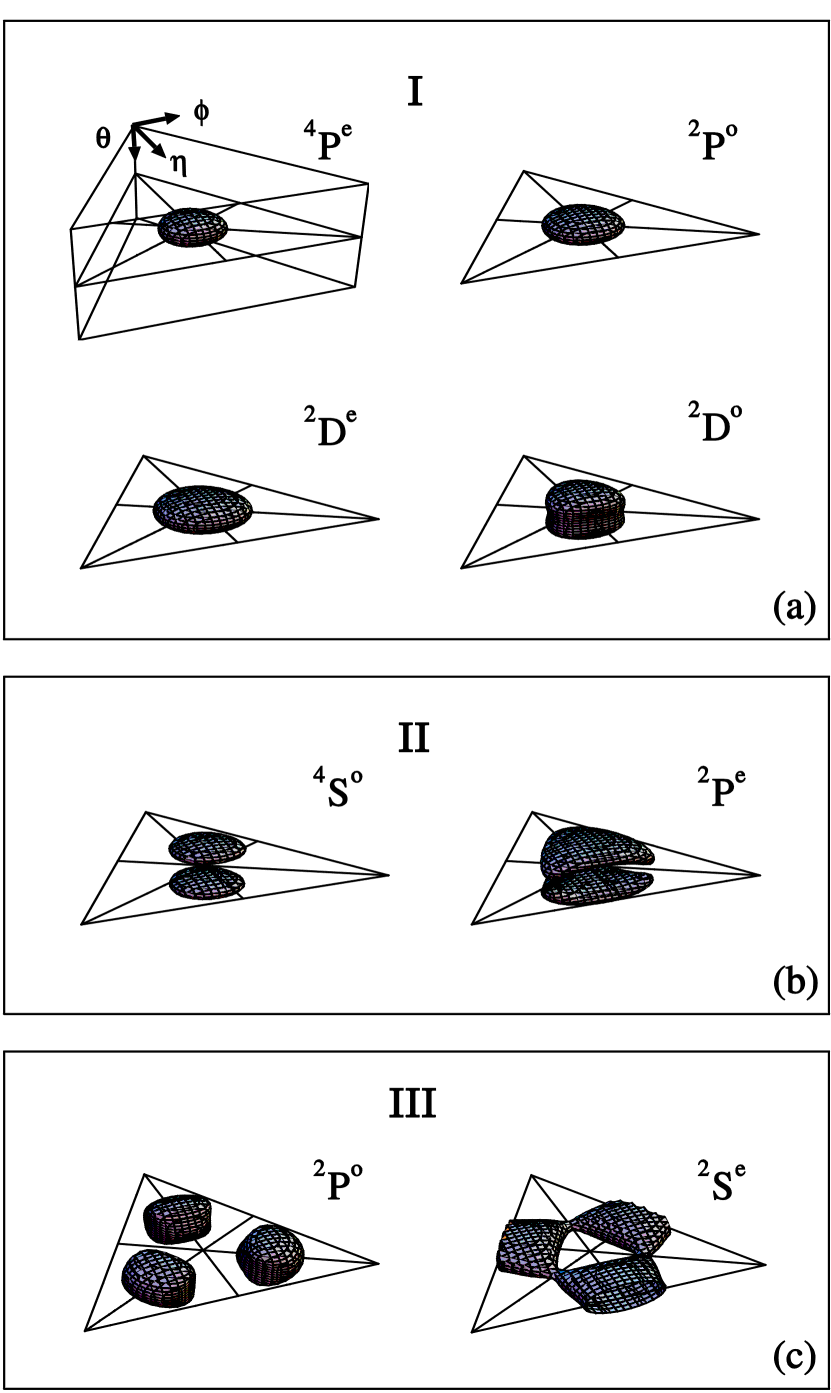
Aren't they gorgeous? Some of them even look alike!
The eight states form three groups:
Group I:
The four pictures imply that the three electrons form an equilateral triangle. In other words, the electrons and the nucleus are arranged like a BF3 molecule. The four states can be viewed as the rotational excited states of a symmetric top which has the shape of an equilateral triangle.
Group II:
The pictures show that the three electrons can form an equilateral triangle but they can not be coplanar with the nucleus. They have the geometry like NH3 molecules.
Group III:
. These two states the three electrons can be coplanar with the nucleus but the three electrons cannot form an equilateral triangle. One can think that the two electrons perform in and out hinge motion with the third electron fixed, or that the two electrons are fixed but the third electron performs swing motion with respect to its equilibrium position which is a forbidden equilateral triangle. We are not aware of any molecules in the ground state have this geometry.
(more to come)



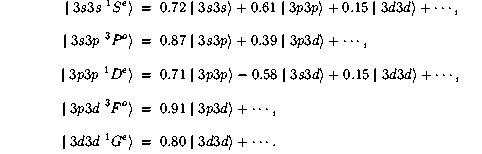

 plane. The nucleus which is at the center of the sphere can lie on this plane. In this case we say the three electrons are coplanar with the nucleus. When it is away from the center, this plane makes an an angle
plane. The nucleus which is at the center of the sphere can lie on this plane. In this case we say the three electrons are coplanar with the nucleus. When it is away from the center, this plane makes an an angle  which is like the latitude on the surface of earth. We further need two angles
which is like the latitude on the surface of earth. We further need two angles
 and
and  to describe the shape of the triangle. These angles are shown here:
to describe the shape of the triangle. These angles are shown here:

