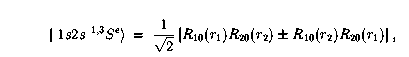
such a function of two variables can be readily displayed on the screen or on a piece of paper. The square of the wavefunctions are shown here:

Consider the simplest atomic system where we need to worry about the quantum symmetry -- the helium atom. Using the conventional wisdom, when a helium atom is excited, one can have one electron in the 1s orbital and the other say in the 2s orbital. The two electrons can couple to form 1s2s 1Se singlet state or 1s2s 3Se triplet state. In what ways are these two wavefunctions differ? Can we see them?
This one is easy, since the wavefunction that depends on the coordinates can be written as
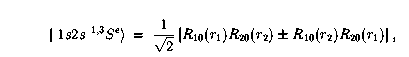
such a function of two variables can be
readily displayed on the screen or on a piece of paper. The square of the wavefunctions are shown here:
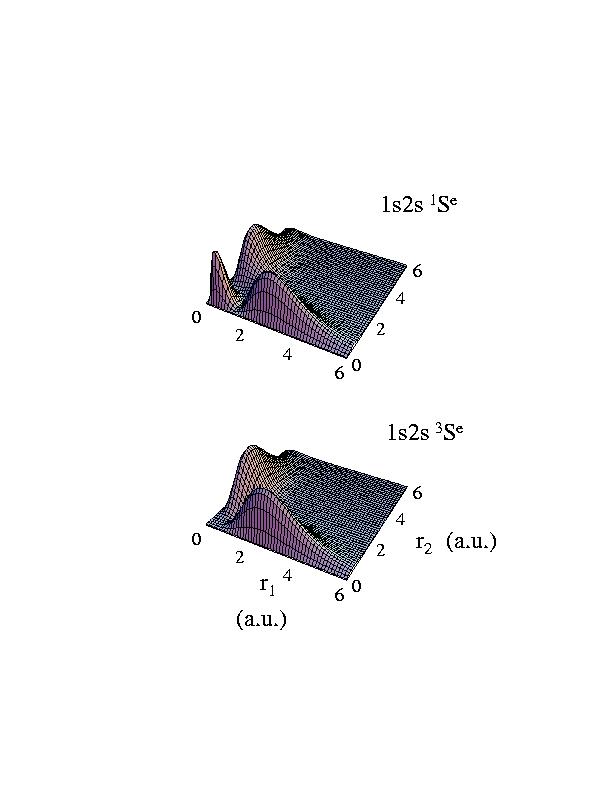
so the difference in 1s2s 1Se and in 1s2s 3Se occurs only in the region where the two electrons are at about the same distances from the nucleus. For the latter the wavefunction vanishes when r1= r2.
The 2p wavefunction has an angular part. The approximate wavefunctions for these two states are:
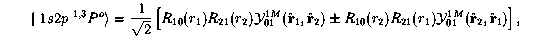
We have immediate problems here since the wavefunctions depend on more than two variables. How do you display the differences between these two wavefunctions?
We do this by displaying the wavefunctions in hyperspherical coordinates defined by
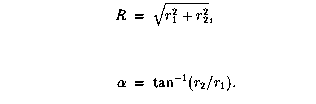
The hyperradius measures the size of the atom, the angle  measures the relative distances of the two electrons
from the nucleus. The wavefunctions above are written in the laboratory frame. To
display the relative positions or distributions of the two electrons we can
average over the rotation of the whole atom.
measures the relative distances of the two electrons
from the nucleus. The wavefunctions above are written in the laboratory frame. To
display the relative positions or distributions of the two electrons we can
average over the rotation of the whole atom.
Now we count the degrees of freedom. We need six coordinates to describe the
positions of two electrons. By averaging over the rotation we are left with three
coordinates. The hyperradius measures the size of the atom. To measure the relative
positions of the two electrons we use the angle  and the angle
and the angle  12 which is the angle between the
two electrons with respect to the nucleus. We can plot the wavefunctions for
each fixed R and see how they depend on these two angles. Here is what you get:
12 which is the angle between the
two electrons with respect to the nucleus. We can plot the wavefunctions for
each fixed R and see how they depend on these two angles. Here is what you get:
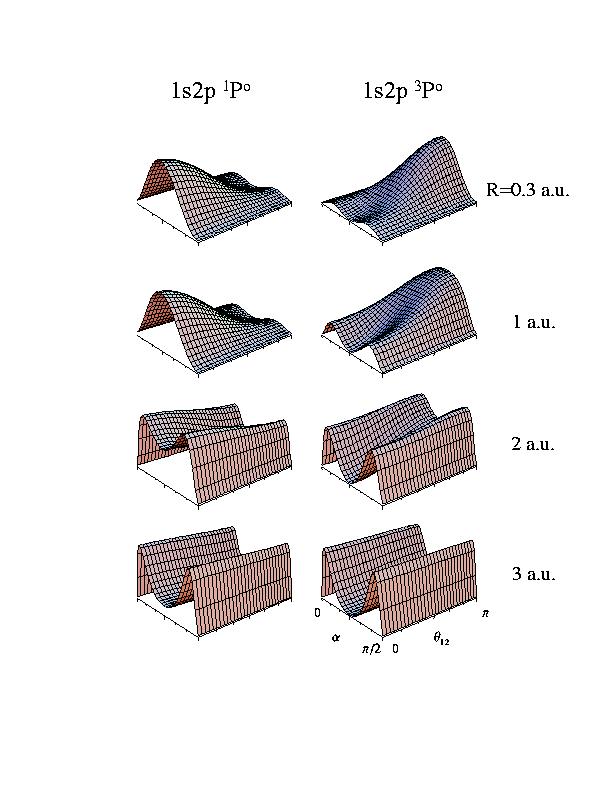
So what does the symmetry do to the relative electronic densities of the two
states. For the 1s2p 1P0 state the two electrons are forced
to stay mostly on the same side of the nucleus. For the 1s2p 3P0
state the two electrons have the chance to stay on oppositive sides of the nucleus.
Interestingly, the symmetry of the wavefunctions are reflected by the "angular
correlation" since the symmetry condition results in different angular dependence
between the two electrons.
Note that symmetry plays no role when the two electrons are not near each other. Thus at large hyperradius, the two wavefunctions are essentially identical. This is always true: symmetry plays a role only when the wavepacket from each electron begins to overlap. When that happens it is meaningless to talk about the wavefunction of individual electrons since no "individuality" exists any more.