Tunnel ionization is when an electron overcomes the potential energy barrier that binds it to the atom and is freed. Lasers can cause ionization by distorting the potential energy barrier so that the electron can tunnel out of the barrier. Double ionization is when this happens twice, and
sequential double ionization is where the first and second electrons each ionize independently of each other and the second electron tunnel ionizes, dominating at strong laser intensities.1 In this project, we examine the phenomena associated with sequential double ionization under the
influence of an ultrashort intense laser pulse.

When laser intensities are strong enough to approach the regime of sequential double ionization (above 6x10¹⁴ W/cm2), the laser profile can become difficult to read. The goal of this project is to create a program that will determine the probability of ionization given these laser pulse
parameters to allow experimental physicists to calibrate their laser beam profiles.

In order to obtain this ionization probability, we begin with parameters such as laser frequency, peak intensity, and pulse duration, and convert these parameters to electric field. Once this is done, we can solve for the survival probability of the atom in two different ways: the
Runge-Kutta method and the integral method. Both methods will allow us to determine the survival probability, and therefore determine the probability of ionization. We choose the element Argon as we have plenty of experimental data to use to verify that our program works as
expected.¹

Step 1. Starting with the laser parameters mentioned above, we can convert these to electric field over time, and then evaluate the ionization rates of these molecules using analytical expression based on tunneling ionization with the Ammosov-Delone-Krainov (ADK) theory. While the ADK theory fails in the barrier-suppression regime, it is sufficient for our purposes when modified. In this project, we use the ADK theory as follows:

 

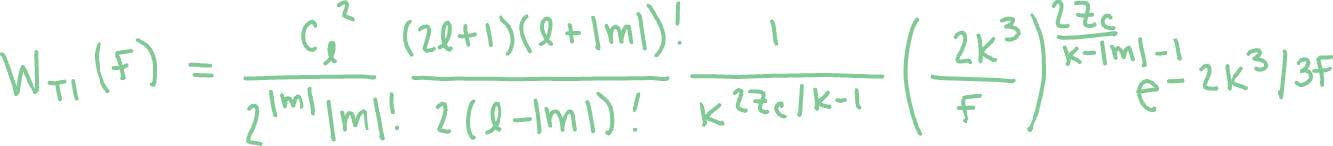
This expression takes in electric field as a function of time, where Cl is the amplitude of the field free bound electron wavefunction in the asymptotic region, l and m are orbital angular momentum and magnetic quantum numbers respectively, Zc is the charge seen by the active
electron asymptotically, and K = √2I_p where I_p is the ionization energy. However, short pulses at higher intensities cause ionization in the barrier suppression regime (at or above the potential energy barrier height), and this results in an overestimation of the ionization rates when using
the ADK method.² In order to correct for this overestimation, we use a modified form of the ADK method with an empirical correction factor as shown:²

 

Here, alpha is a fitting parameter, and W_TI is the expression as given above. Therefore, W_TBI gives us the ionization rate and can be used in the next steps.

Step 2. Next, we use the ionization rate to calculate the ionization yield of Ar+ and Ar2+. There are two methods we used to verify our results in this step. Method 1 involves a standard integration, while Method 2 uses the Runge-Kutta method to solve three linear first order differential equations. Both methods are outlined below.

Method 1: Using the following expression, which is a rate equation for population transfer for the first ionization from Ar to Ar+, where p₀(t) is the survival probability and W(t) is the ADK expression from Step 1.

 

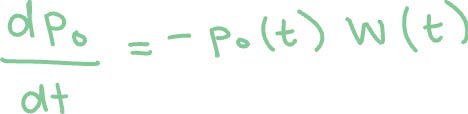
We can solve this equation in the following manner:

 

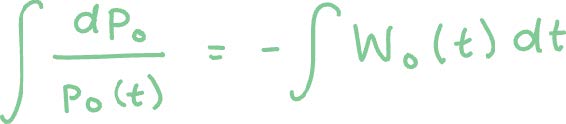
To obtain:

 

Once we have this expression, we can use the scipy.integrate function in Python to solve for p(t). For example, when we use a laser intensity of 7x10¹⁴ W/cm² with a pulse length of 4fs (or 164a.u.) and a wavelength of 750nm, we get:
p₀(t) Ar: 0.5314800911592326
p₁(t) Ar+: 0.469

P₀ and p₁ are the survival of Ar and Ar+ respectively. In order to get the ionization probability we subtract these factors from 1, since the ionization yield is given by 1 - p(t). So the Ar2+ yield is 1 - 0.9947161003161279 (the sum of p₀ and p₁), which gives p₂ to be 0.00528389968387.

Method 2: Using the Runge-Kutta method to solve the following first order linear differential equations.³ Here p₀(t) and p₁(t) are the survival probabilities of Ar and Ar+, respectively, and W₀(t) and W₁(t) are the ADK expressions with respective factors for each ionization.

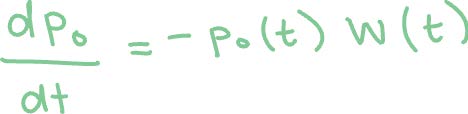
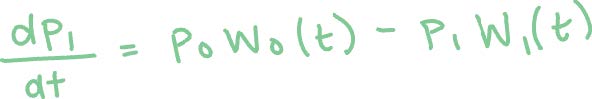
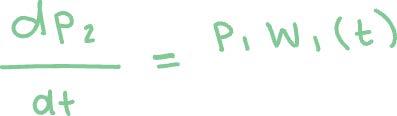
The Runge-Kutta method is an iterative method that takes an initial value problem with some initial condition. In our case, the initial conditions are p₀(0) = 1 and p₁(0) = 0 since there are no Ar+ ions at the beginning of the laser pulse. The rate of change (dp/dt) is a function of t
and p itself. A maximum step size of 1 is chosen, and each iterated value is determined by the previous value plus the weighted average of four increments. Each increment is the product of the size of the interval and its height, or slope.⁴

Using this method and the same laser profile, we obtain the following:
p₀(t) Ar: 0.53124674
p₁(t) Ar+: 0.46
p₂(t) Ar2+: 0.0014

We can see that for p(t) Ar, both methods agree to 3 decimal places to give us 0.531. It is important to note that the population of the state is also the probability of finding the system in that state.

Fig. 1: Survival Probability of Ar, Ar+, and Ar2+ Over a 4fs Pulse

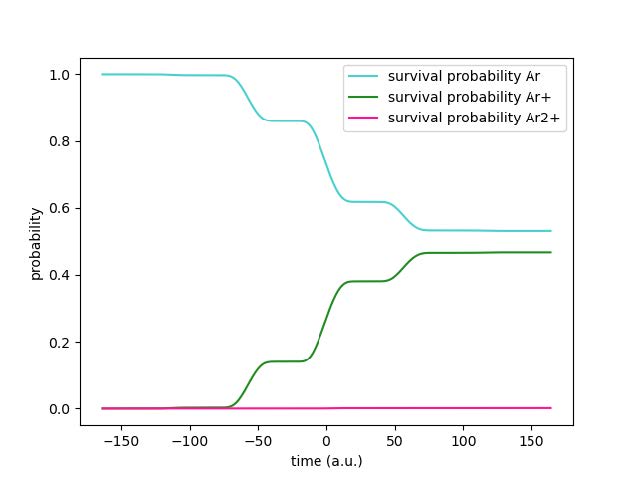
Additionally, it is important to note that the curve has waves due to the fact that tunneling electrons are emitted in bursts near the maxima and minima in the oscillating electric field produced by the laser. The time is converted to atomic units from a 4 femtosecond pulse, with
the maximum strength of the laser at time 0. The above graph was obtained using Method 2.

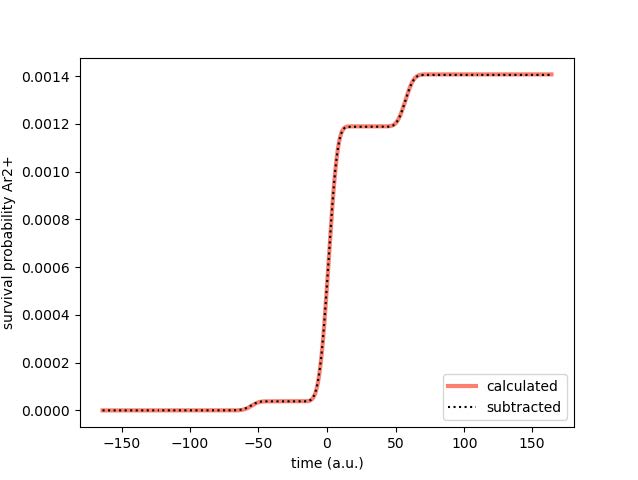Fig. 2: Survival Probability of Ar2+ Over a 4fs Pulse

 

Here we note that while previously it looks as if there is no survival probability for Ar2+, that is not the case. The pink line comes directly from using the Runge-Kutta method to solve for p1 in the third differential equation above, while the black dotted line is obtained by solving for the survival probabilities of p₀ and p₁ in the previous two differential equations and then subtracting them from 1. All three survival probabilities (for Ar, Ar+, and Ar2+) add up to a complete ionization probability of 1. There is a slight error of less than 5x10^-3 in the calculated survival probability from the Runge-Kutta method, which is expected.

Step 3. Finally, using both of these methods, we can obtain the probability of ionization by subtracting each survival probability from the total ionization probability of 1, or

Ionization = 1 - p(t).

This is done for a range of strong intensities in the sequential double ionization regime, from approximately 0.5x10¹⁴ to 2x10¹⁵ W/cm².

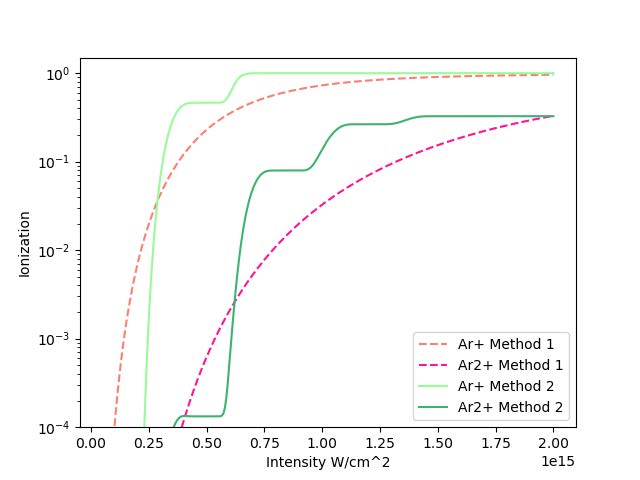
In this graph, the dotted pink lines are obtained from Method 1 (integral method) while the solid green lines are obtained from Method 2 (Runge-Kutta method). The solid green lines seem to overestimate the ionization over the intensity range and jump unexpectedly. Since this does not
match the results obtained from Method 1, more consideration should be given to this method in future work to better calibrate the program.

The end result of this project is the program that we built to create this last graph. This program still needs a few adjustments to properly calculate ion yields using the Runge-Kutta method; however, it takes in laser pulse parameters and converts these to electric field data, which can be used to find the ionization rate, and subsequent probability of survival and ionization. Future work would include fine-tuning this program to fix the error above, as well as testing other intensity ranges to be sure it is calibrated correctly.

References
¹Kubel, M. et al. “Complete characterization of single-cycle double ionization of argon from the nonsequential to the sequential ionization regime.” Physical Review A 053422-2 (2016)
²Tong, X.M., Lin, C.D., “Empirical formula for static field ionization rates of atoms and molecules by lasers in the barrier-suppression regime.” Journal of Physics B: Atomic, Molecular, and Optical Physics. 2595 (2005)
³Lin, C.D., Yuen, C.H., “Density-matrix approach for sequential dissociative double ionization of molecules” Physical Review A 023120 (2022)
⁴“Runge–Kutta Methods.” Wikipedia, 23 July 2023, en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods.

Acknowledgements

I would first like to thank Professor C.D. Lin and Isaac Yuen for their mentorship, patience, and commitment to helping me improve as a physicist throughout the course of this project as they welcomed me to their team. I am grateful to Kim Coy, J.T. Laverty, and Loren Greenman for their roles in organizing this program and assisting me with kindness, as well as Kansas State University and the National Science Foundation for funding this unforgettable experience.

Final Presentation