The generation of ultra-fast, intense laser pulses for various applications has been approached from many different angles. Complimentary to quantum approaches towards generating these laser pulses, I have looked for solutions through classic mechanical approximations. An atom in a laser field has a chance of becoming ionized due to the electric field component of the laser altering the potential the electron experiences. Once ionized away from the atom the electron is then a free floating, charged particle in an electric field. Therefore this electron undergoes a force and travels along a trajectory. The electric field of the laser alternates direction over time so eventually, depending on the strength, the electric field can cause the electron to return to the atom. Upon returning, if recombination occurs, the kinetic energy gained by the electron traveling through the electric field is released as a photon. The goal of my project is to analyse different laser systems to find what parameters, such as laser intensity, multicolor waveforms, orientation of laserfields, etc., can optimize the energy of the produced photon and in what time intervals. I do this by setting up a Newtonian equation of motion for the force the electron experiences, then using a Runga-Kutta method to solve for the electron's trajectory and thus calculating the kinetic energy aquired upon returning to the nucleus.The developing of optimized parameters to produce ultra-fast, and intense laser pulses would benefit a variety of different fields of science.

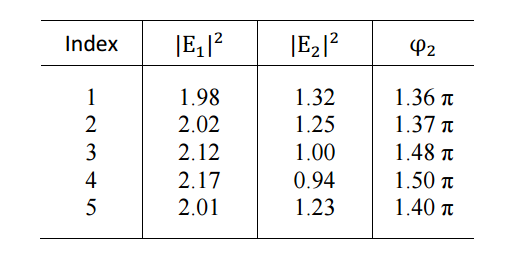
  A paper was published in 1997 by M Protopapas et al. describing a classical approach to solving the Newtonian force equation for a single laser ionizing a hydrogen atom. By setting up the force equation the electron experiences and solving for the trajectory through calculus, M Protopapas et al. were able to produce an, 'Impact Kinetic Energy Curve' that describe the amount of return kinetic energy an electron had depending on when along the laser field the atom was ionized. The wavelength and intensity of the laser was fixed at 800 nm and 10¹⁴ W/cm².

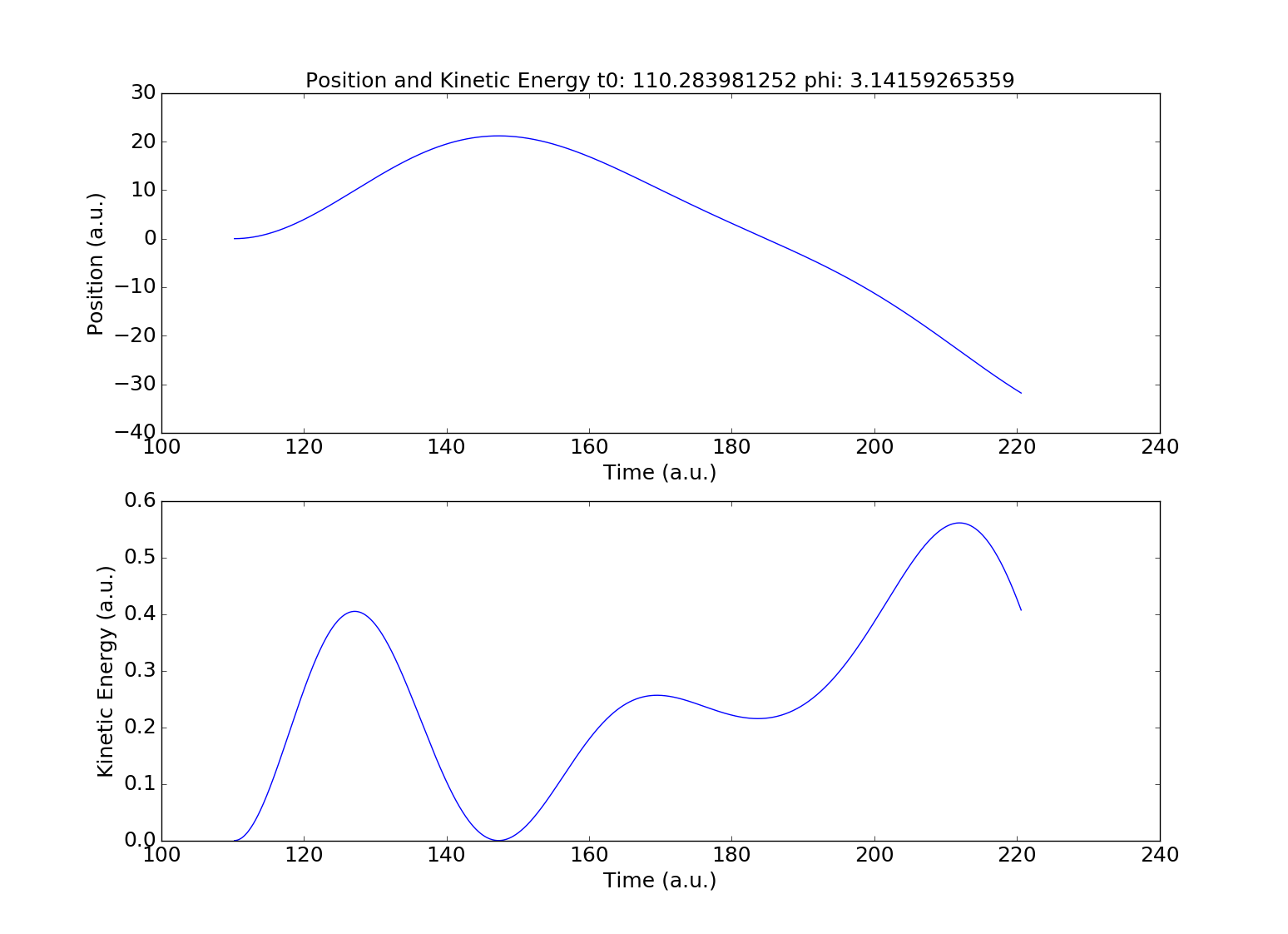
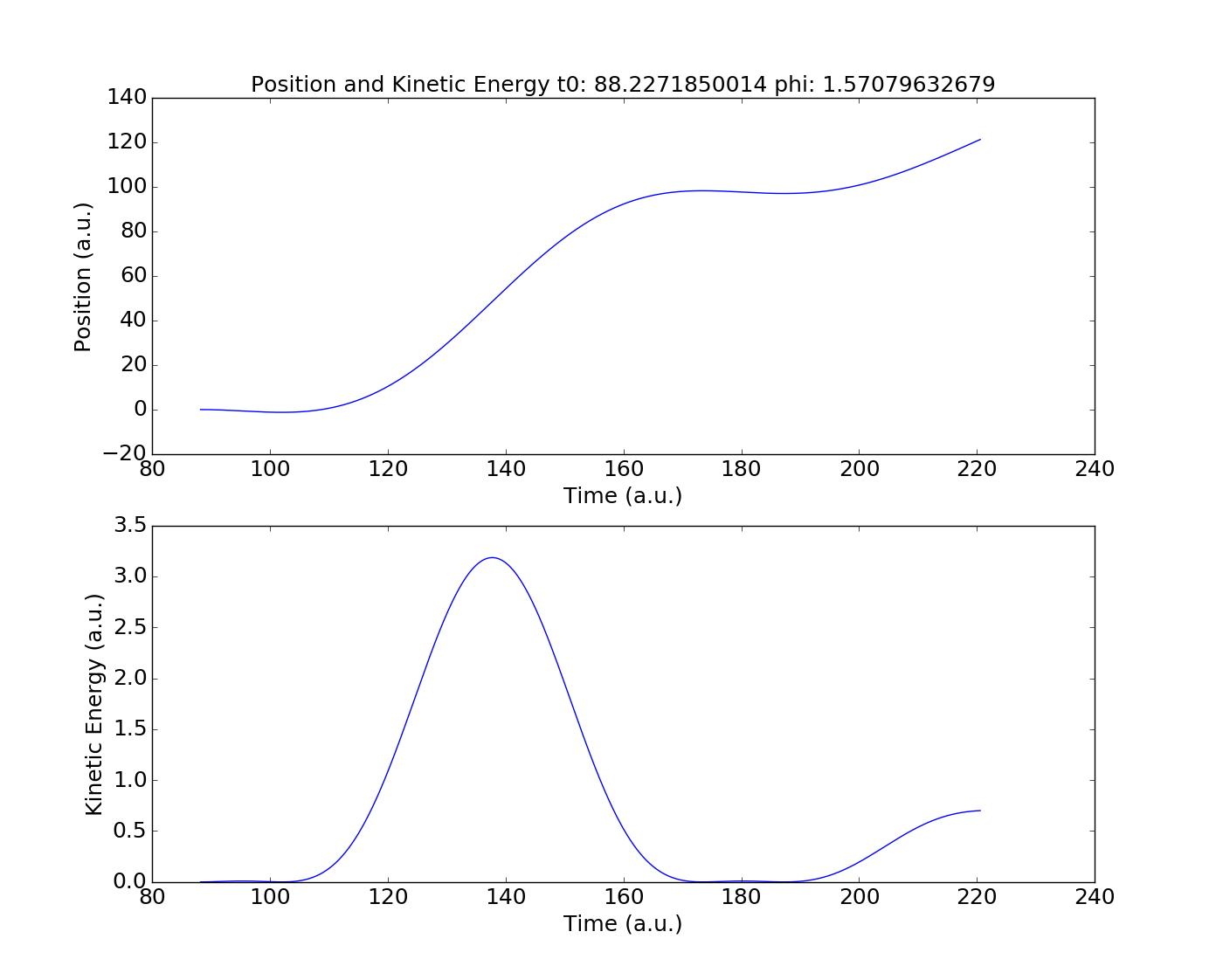
  In order to ensure my understanding of the project, and then later to test my Runga-Kutta method (RK4) of solving for the electron's trajectory my first step in this research project was to replicate this paper's results. Below is the Kinetic Energy curve of the paper (on the left) and my RK4 method (on the right).

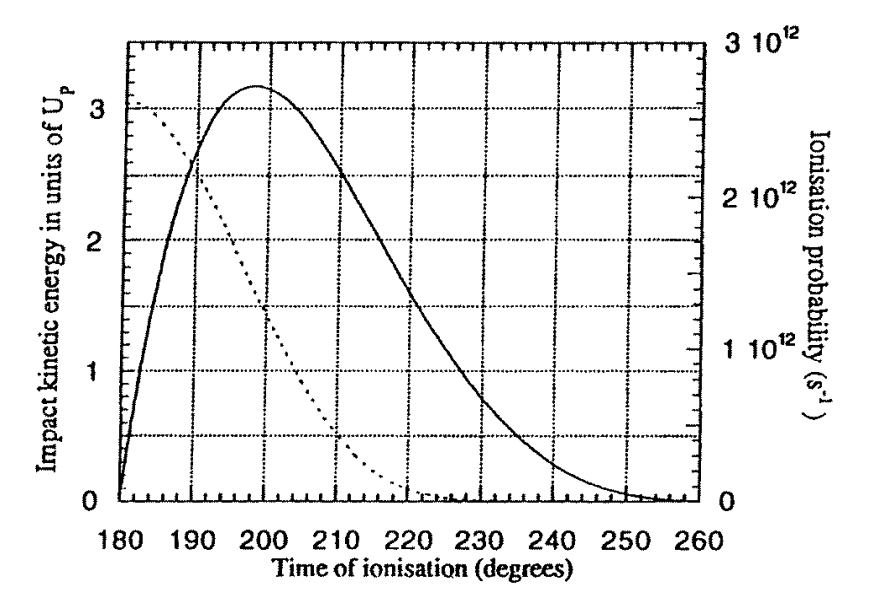
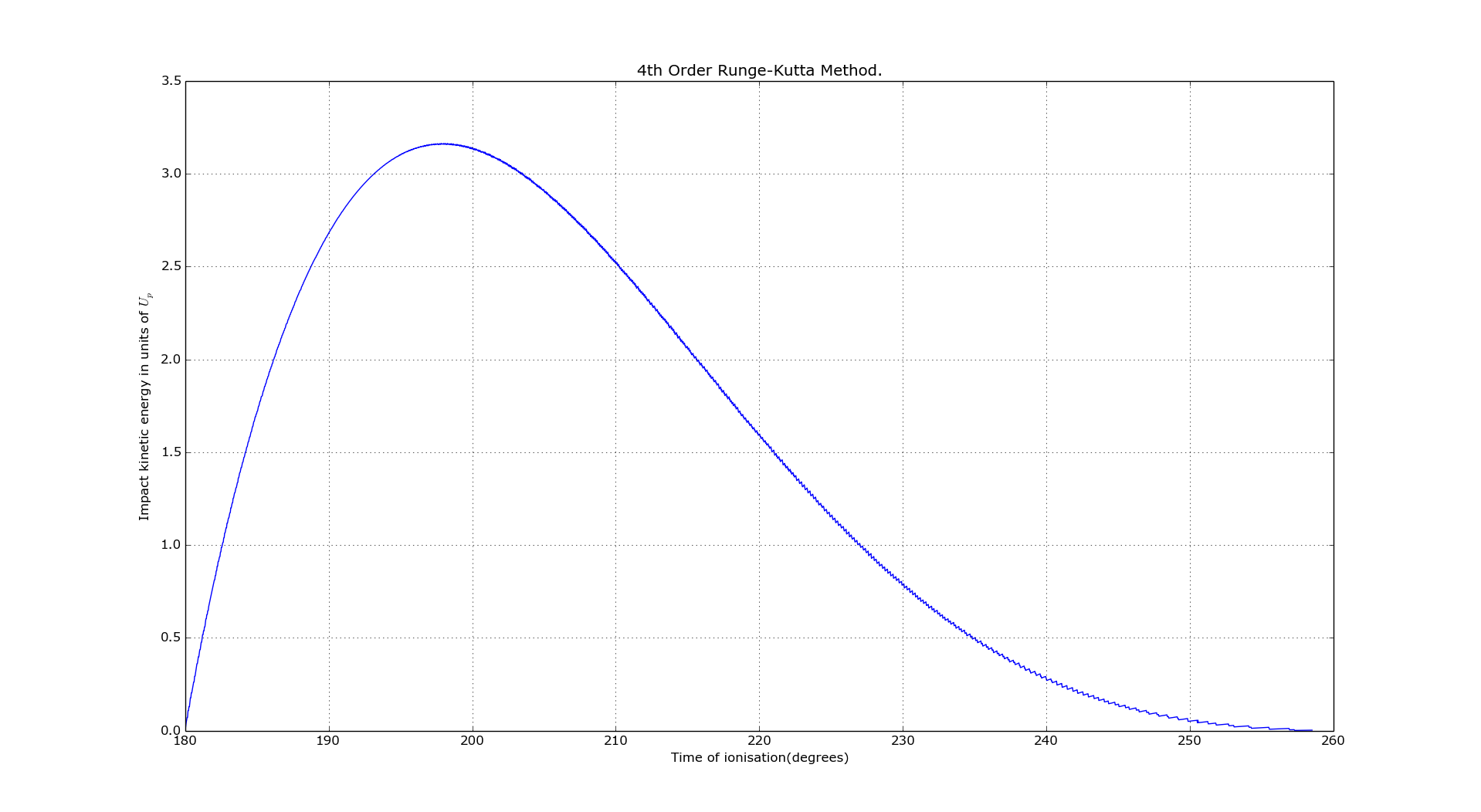
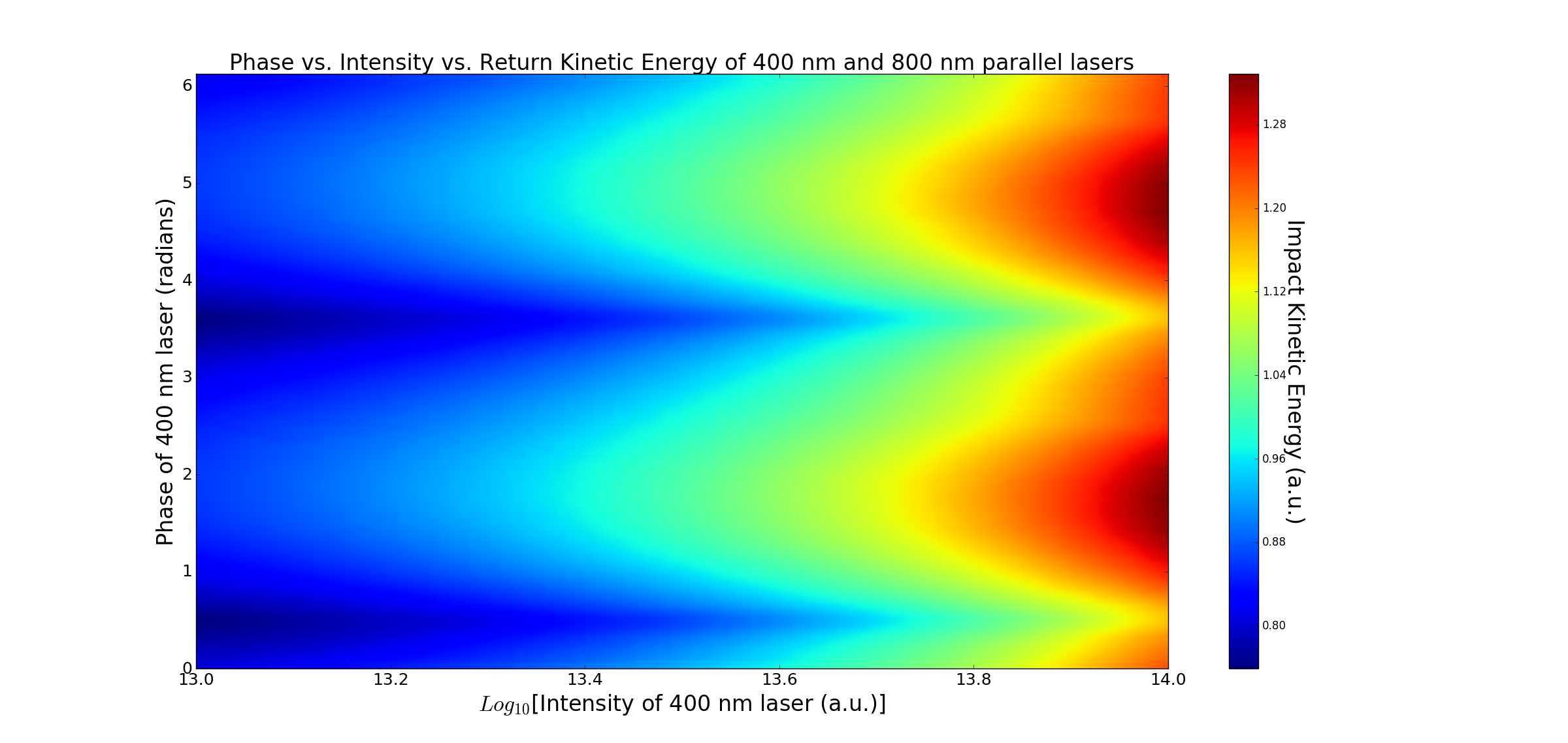
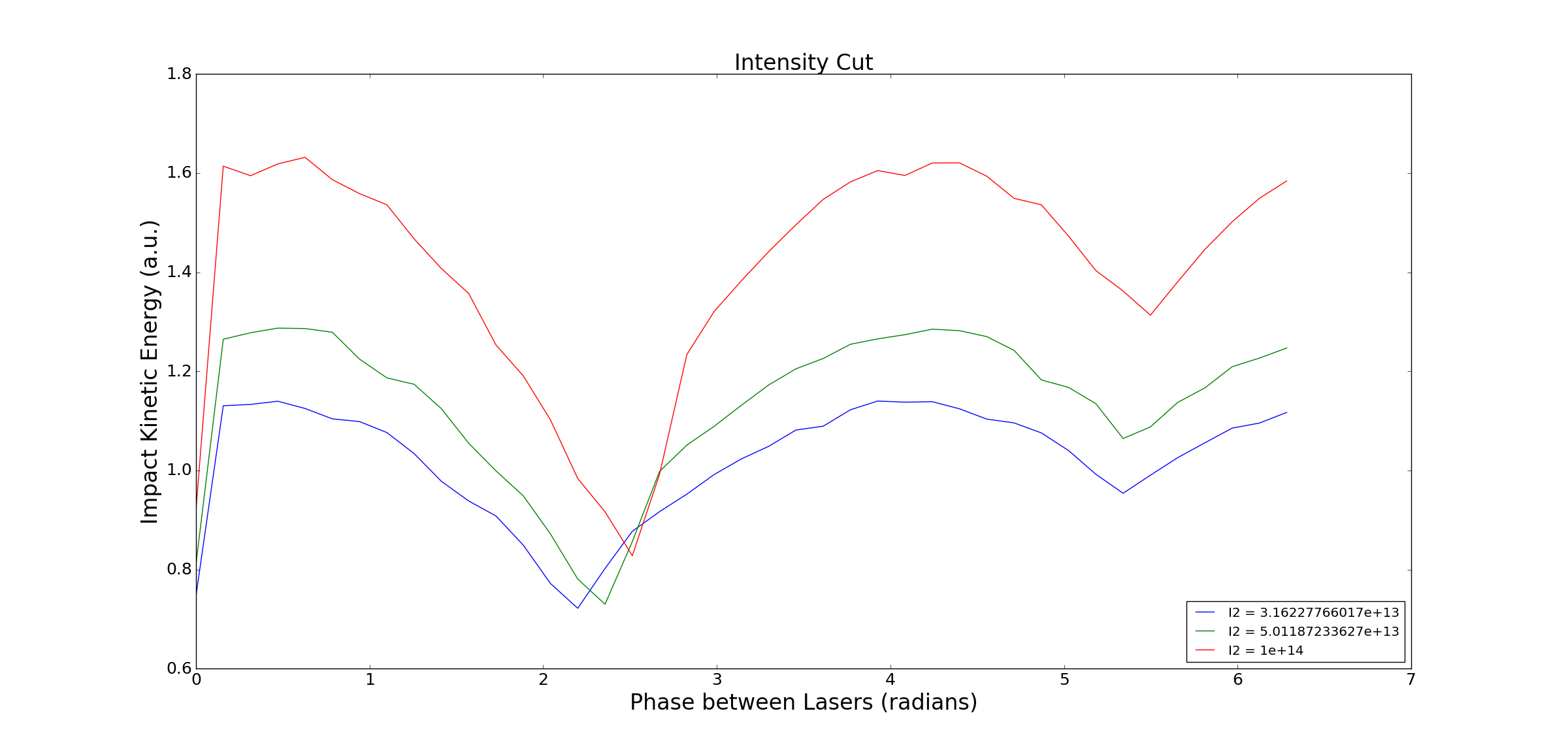
  As seen from these graphs my RK4 method reproduced the results of the paper and from here we can apply the same method to different laser systems. The first laser system I'll analyze, and it happened to end up being the only one for now, is two lasers of varying wavelengths, linearly polarized, and parallel with one another. The results we received from this analysis prompted more questions that needed answered before moving on and those questions lead to more interesting results.

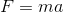  The initial simulation that I pursued was two lasers of equal intensity, linearly polarized, their polarizations being parallel with one another and one laser having a wavelength of 800 nm and the other having 400 nm. Allowing these two lasers to lie on one another would create a combined E-field that would be used in the analysis. Starting with the Newtonian equation ; the force the electron feels by the E-field of the laser is the charge of the electron (in atomic units) e = 1 multiplied by the electric field itself. Approximating the E-field as: 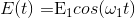for the first laser and then the combined E-field equation is: 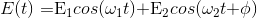where each ω represents the angular frequency of each laser based on their wavelength and ψ represents the phase between them. Now dividing the last equation by the mass of the electron (in atomic units) m = 1 then we have our acceleration equation: .

  Since the accelaration equation is simply the second derivative of the position function I can use my RK4 method to solve for it. The solutions my RK4 will produce will depend on the initial conditions I give the system. The initial position and velocity of a 'birthed' electron when it is ionized from the atom has a mean value of 0 for each and I therefore assume these values for this system. However 'when' the electron is ionized from the atom is important and can be variable. I will refer to this, 'time of ionization,' as t0 and each t0 will produce a different trajectory. When analyzing these trajectories I am interested in when the electron returns to the nucleus, if ever, and when it does so with what kinetic energy? Since the trajectory is altered depending on what t0 I choose I decided to scan through all t0s from 0 to one full period of the largest wavelength laser. Below are some examples of these trajectories.

  Analyzing hundreds of these trajectories included finding when/if a zero occurred, in other words; when the electron returned to the nucleus. Once all zeroes have been found my RK4 method allows me access also to the velocities at those points meaning I can calculate the kinetic energy the electron had upon returning. Doing this while varying the phase of the two lasers with respect to one another, varying the intensity of the 400 nm laser, and scanning through different times of ionizations allowed me to optimize the trajectories to give me the highest amount of kinetic energy given the previously mentioned parameters.

   Many different results were concluded from this anaylsis and upon investigating the data gathered. The two most interesting results would include seemingly an independence between the phase and intensity of the two lasers, and a hint in accuracy of my classic method of finding these kinetic energies.

   The following figure shows a Phase vs. Intensity vs. Max Return Kinetic Energy graph of the two lasers, 800 and 400 nm. What we can see from the graph is that the phase location of the maximum return kinetic energy seems to not depend on intensity. If we were to take cuts at different intensities we would see that the max KE occurrs at the relatively the same phase for all intensities. The figures following the 3d surface plot is an example of those cuts.

   The next results occurred when I changed the wavelength parameter of the two lasers to be 1600 nm and 533 nm. This was done to match a paper published in Nature by Cheng Jin et al. in 2014 titled, "Waveforms for optimal sub-keV high-order harmonics with synthesized two-or-three-colour laser fields." In this paper this approach to this type of analysis was done via quantum mechanics. One such table from this paper depicts a set of five maximum kinetic energies of these two lasers, with varying intensities, and at what phase does the maximum occur. The following two tables shows the one previously mentioned and a table my method produced respectively. My table shows the maximum that I found also occurring at the same average phase as the quantum approach. The intensities differed between the two methods as we were optimizing our lasers for different purposes so it is curious that even with different intensities the same phase was developed for the maximum. This could also indicate my classical approach could very well be used as an alternative to the computationally heavy quantum approach.

  To summarize my results; my figures and my table demonstrate the possiblity of using a classical approach to solving for kinetic energies in these laser systems. My method matched the results of Protopapa et al. and Jin et al. My results also show seemingly an independence between intensity and phase when calculating the max return kinetic energy.

  My name is Darren Lee Woodson II. I am a senior attending Kansas Wesleyan University in Salina at the time of creation of this website. I am majoring in Mathematics, Physics, and Computer Information Systems. I plan on obtaining my PhD in Physics and hopefully obtaining a job doing research in space science.

• Jin, Cheng, Guoli Wang, Hui Wei, Anh-Thu Le, and C. D. Lin. "Waveforms for Optimal Sub-keV High-order Harmonics with Synthesized Two- or Three-colour Laser Fields." Nature Communications Nat Comms 5 (2014): n. pag. Web.
• M Protopapas et al 1997 Rep. Prog. Phys. 60 389 n. pag. Web.

  This work is partially funded by the National Science Foundation (NSF) and the Air Force Office of Scientific Research (AFOSR) through NSF grant number PHYS-1461251. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the NSF or AFOSR.

  This work was partially supported by an NSF EPSCoR IRR Track II Nebraska-Kansas Collaborative Research Award (1430519).