|
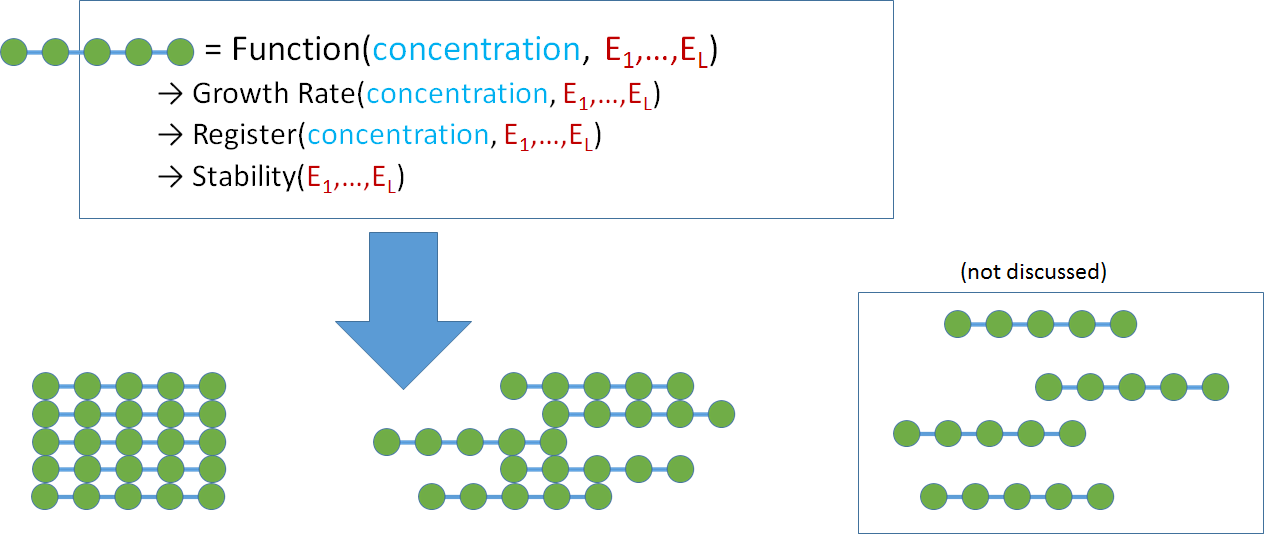
Theory of Sequence Effects and Concentration on Protein Aggregation in Amyloid Fibrils by Caleb Huang Principal Investigator: Dr. Jeremy Schmit, Associate Professor of Physics Kansas State University Physics Department REU Program OverviewMy research this summer primarily involves developing analytical theory for binding properties of the amyloid fibril, which is a sheet of aggregated proteins that causes various common diseases such as Alzheimer’s disease, Parkinson’s disease, and type 2 diabetes. In short, I translate protein structures and dynamics, which are notoriously complex, onto a piece of paper. The running joke among theoretical physicists is to introduce the premise of an argument by “assuming a spherical cow.” This is an apt description of what I do: I first strip the properties of proteins to its fundamentals, and add new variables piece by piece. Fundamentally, I want to answer why some proteins are more prone to aggregate than others and what factors influence how they aggregate. Research Description is an extended summary of my project. It is meant to be understandable to the general science-educated public. REU Social Life discusses the REU experience outside of research. About Me gives a brief bio about my background in physics and school.
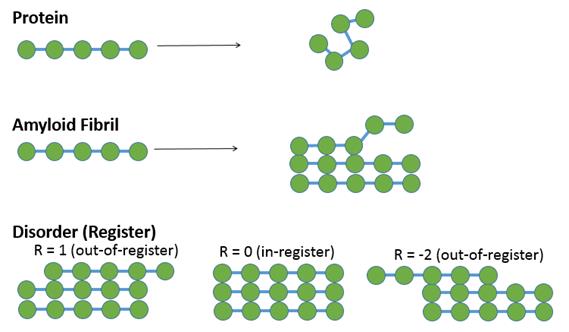
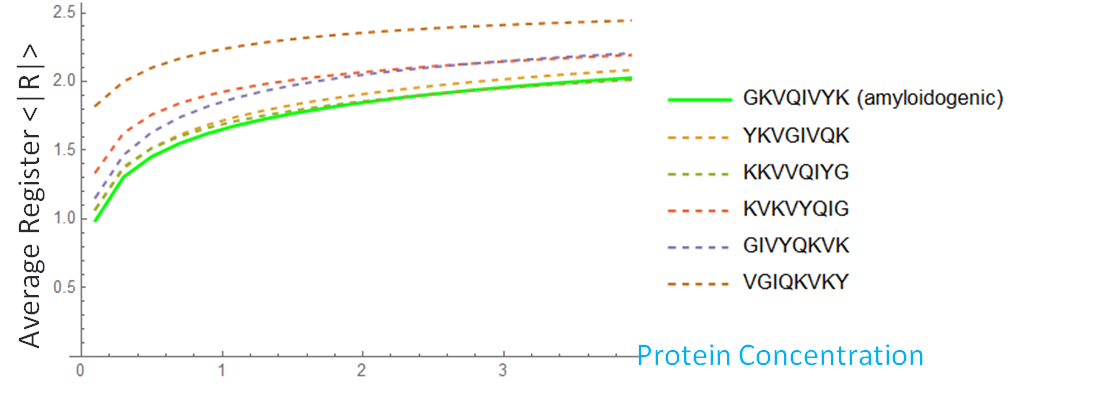
Figure 1: The theoretical physicist’s perspective of the amyloid fibril. Research DescriptionAmyloid Fibril and DiseasesUbiquitous in living organisms, the protein is an organic polymer consisting of a sequence of various amino acids. It typically folds into a three-dimensional structure after being synthesized. Depending on its sequence, it may serve various functions such as communication, structural support, and transport. However, under certain circumstances, the protein does not fold properly but instead binds onto another protein via hydrogen bonds along the protein backbone. The formation results in a crystalline sheet of proteins called the amyloid fibril, which is the cause for various diseases such as Alzheimer’s disease, Parkinson’s disease, and type 2 diabetes. The register is a metric for polymer alignment, a key property that affects biochemistry of aggregates in vivo and therefore their physiological effects on the body. Amyloid fibrils tend to be close to in-register, whereas disordered protein aggregations form non-fibrillar amorphous “glops.” Current understanding on the properties of amyloid fibril formation is mostly experimentally determined and case-specific. The goal of this project thus is to construct a theoretical framework to determine general principles of amyloid fibril formation.
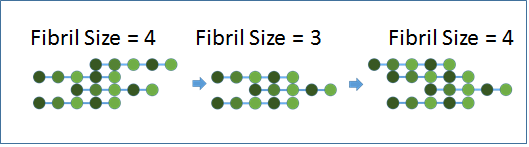
Figure 2: Cartoon illustrations of protein aggregation.
Biased Diffusion ModelFundamentally, the amyloid fibril is nothing more than polymers hydrogen bonding to each other. The different properties in the amino acid is captured by differences in binding energy. For example, polar amino acids tend to be weakly binding, whereas nonpolar amino acids tend to be strongly binding due to entropic effects. Binding energies work in opposition to thermal energy and dictate how fast the bonds break. Qualitatively, positive binding energy favors forward binding (difficult to unbind), neutral binding energy has no effect (unbinding process purely thermodynamic), and negative binding energies favors unbinding (easy to unbind).
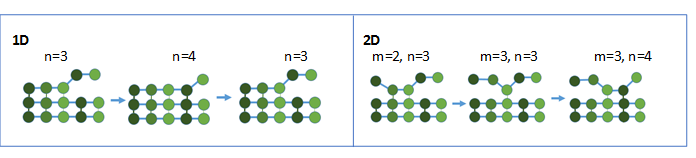
Figure 3: The dissociation rate of the n-th amino acid, k-,n, is dictated by the binding energy. Toy Models Describe Binding DynamicsMicroscale Binding (Amino Acids) The binding and unbinding dynamics can be modeled using the discrete random walk model. Intuitively, for moderate binding energies, the biased “walk” can be visualized as a dance where the polymer takes a few steps forward while taking a step back occasionally. The 1-D random walk is solvable analytically and provides insight on the relation between energy and the residence time (how long the polymer sticks). The 2-D model is only solvable numerically but is a more accurate representation of polymer behavior.
Macroscale Binding (Proteins) The information from the microscopic view of amino acid binding is incorporated in the macroscopic scale of protein polymer binding, namely the polymer off rate, denoted koff(E1,…,EL,R). The off rate depends inversely on the residence time at binding, t1(E1,…,EL). The polymer on rate, kon(c, L), follows general diffusion rules and is proportional to concentration. While energy dictates how long a polymer stays, concentration dictates how rapidly polymers meet.
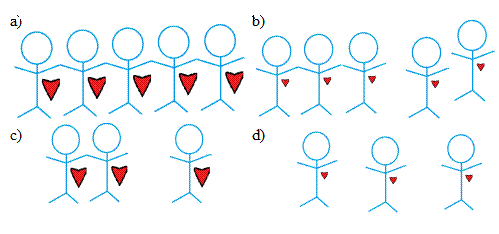
Polymer aggregation is concentration- and energy-dependent. It is roughly analogous to a polyamorous dating game, where each polymer represents a “person” with a certain “attraction” to others. Finding mates requires both a considerable number of opportunities to meet available candidates and a high mutual attraction factor. However, a high concentration of polymers can compensate for low attraction and vice versa.
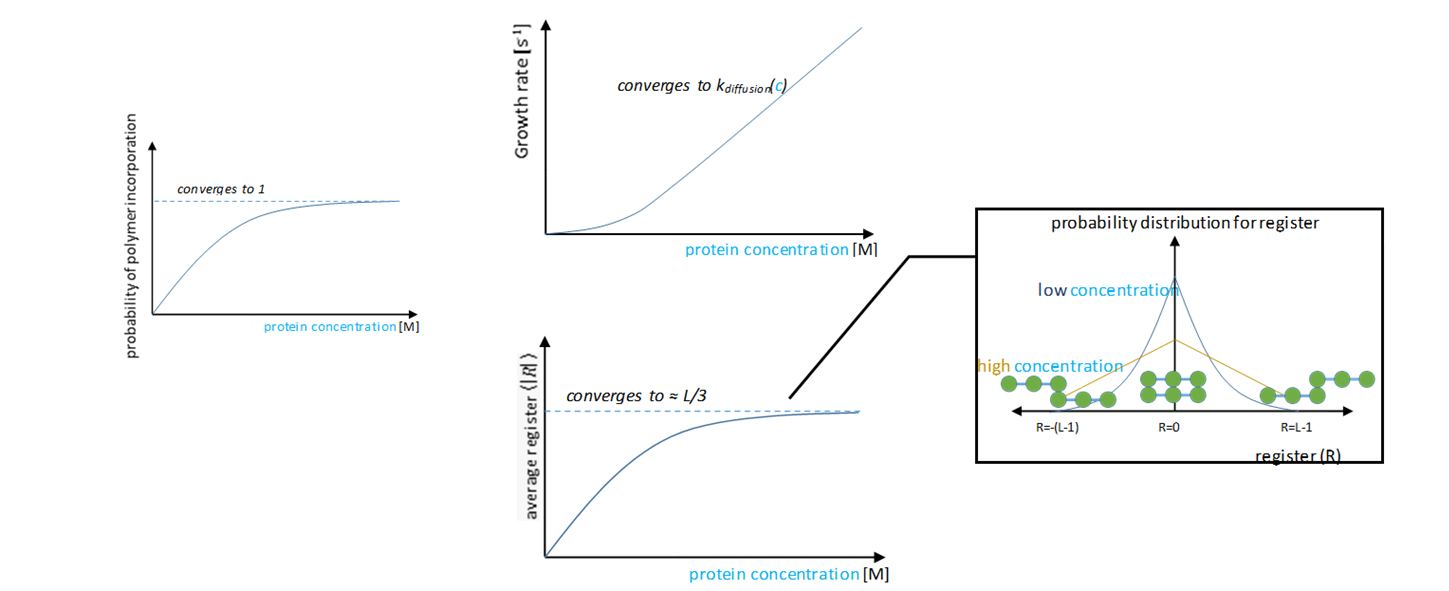
Figure 4: a) High concentration and high attraction lead to high rates of aggregation. b) High concentration and low attraction lead to medium rates of aggregation. c) Low concentration and high attraction lead to medium rates of aggregation. d) Low concentration and low attraction lead to low rates of aggregation. The probability of polymer binding converges to one at infinite concentration. Our model predicts that the growth rate converges to the diffusion rate and that the register converges to approximately L/3 for polymers of length L. At high concentrations, high registers (disordered states) are less selected against (Figure 5 inset). This shows that our model fits well-known theory: generating well-ordered crystals requires time. However, different proteins aggregate differently even under similar conditions in the body, say equal concentrations and temperatures. Here, we assume that all amino acids have equal binding energies. But, as previously discussed, what distinguishes one protein from another is its unique sequence of amino acids. Importantly, this affects the probability distribution of registers.
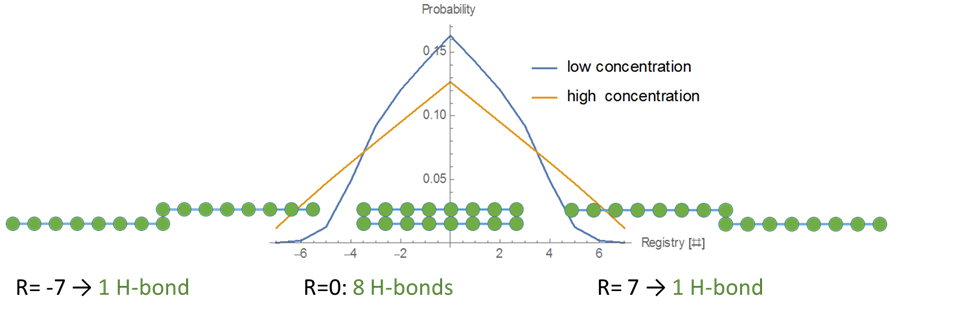
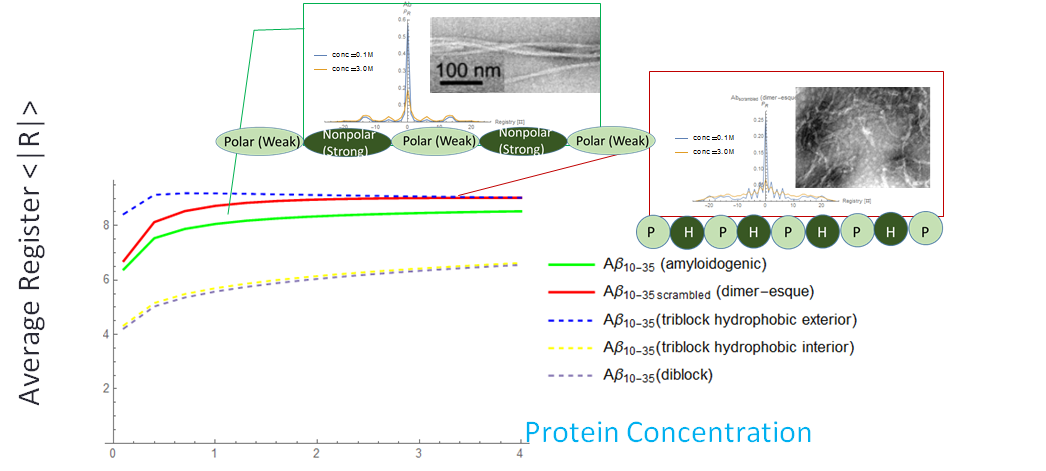
Figure 5 Varied Binding Energies: Nature’s Favored Search AlgorithmFor uniform binding energies, off-register binding is energetically less favorably simply due to fewer hydrogen bonds. At R=0, there are eight hydrogen bonds, whereas at R=7, there is only one. The polymer off rate, koff, increases exponentially as the register increases, thus lowering the binding probability of high registers (by the probability of polymer incorporation model, the binding probability falls off roughly proportional to 1/(1+e|R|)). However, there are no additional energy penalties or gains for off-registers.
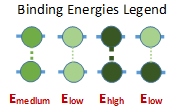
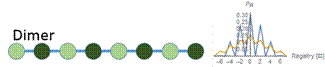
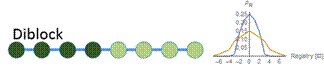
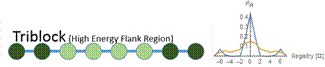
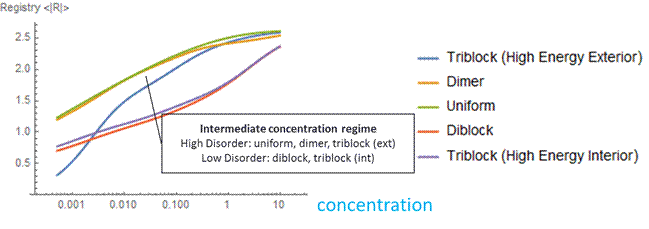
Figure 6: At a low concentration (blue), the probability distribution is a larger peak centered around zero. At a high concentration (yellow), the probability distribution is wider, and higher registers are more likely. We vary the energy distribution while keeping the total binding energy constant. One method to find distributions that give maximum and minimum disordered states is to perform a constrained search optimization. To solve for the behavior of distributions in between, we directly check certain energy distribution motifs. We assume that the dark green circles are nonpolar amino acids and the light green circles are polar amino acids. Established theory tells us that nonpolar amino acid pairs bind strongly, polar amino acid pairs bind weakly, and polar and nonpolar amino acids pairs bind weakly. For the dimer energy motif, the R=1 binding state thus becomes highly unfavorable with all weak bonds, while R=2, like R=0, has alternating weak and strong bonds. The triblock with high energy exteriors follows a similar trend. For the diblock and triblock with interior high energies, the low registers are favorable while high registers are highly unfavorable. |

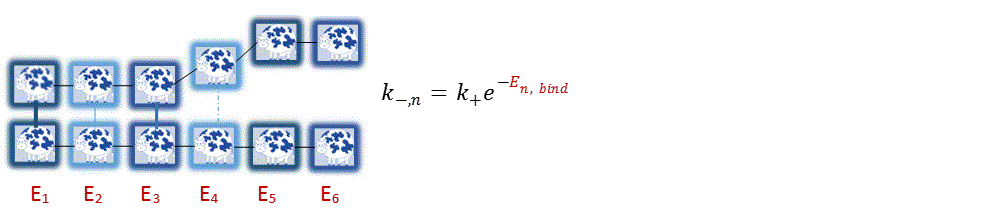
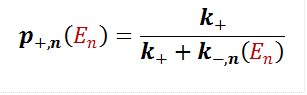
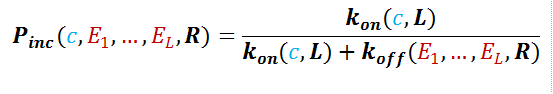




 This program is funded by the National Science Foundation
through grant number
This program is funded by the National Science Foundation
through grant number