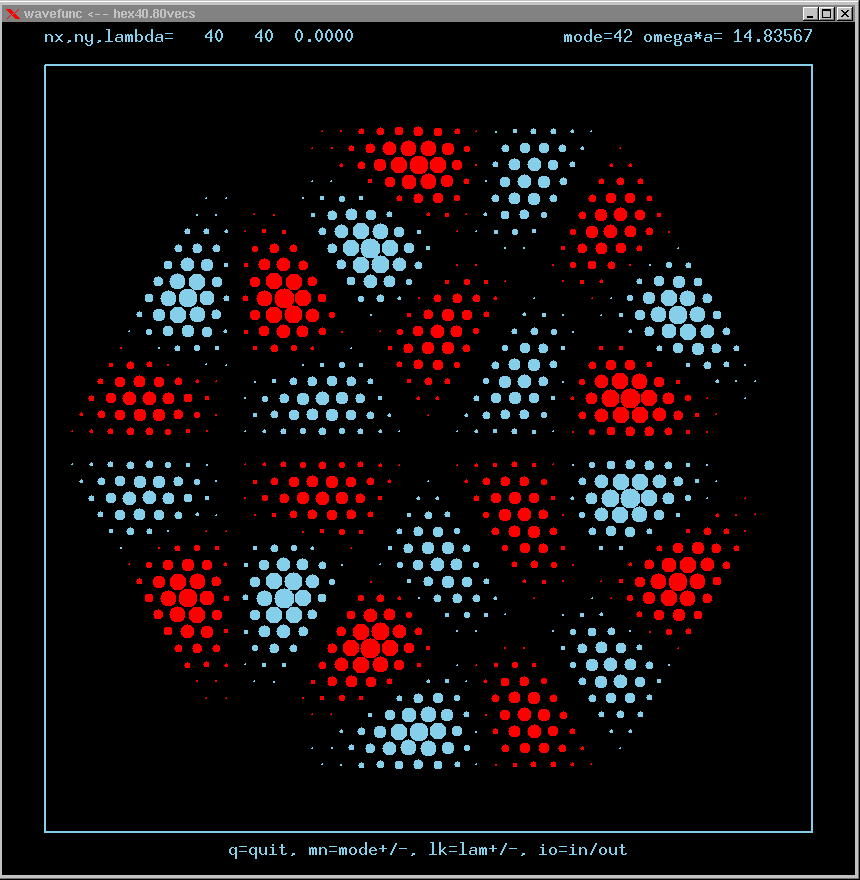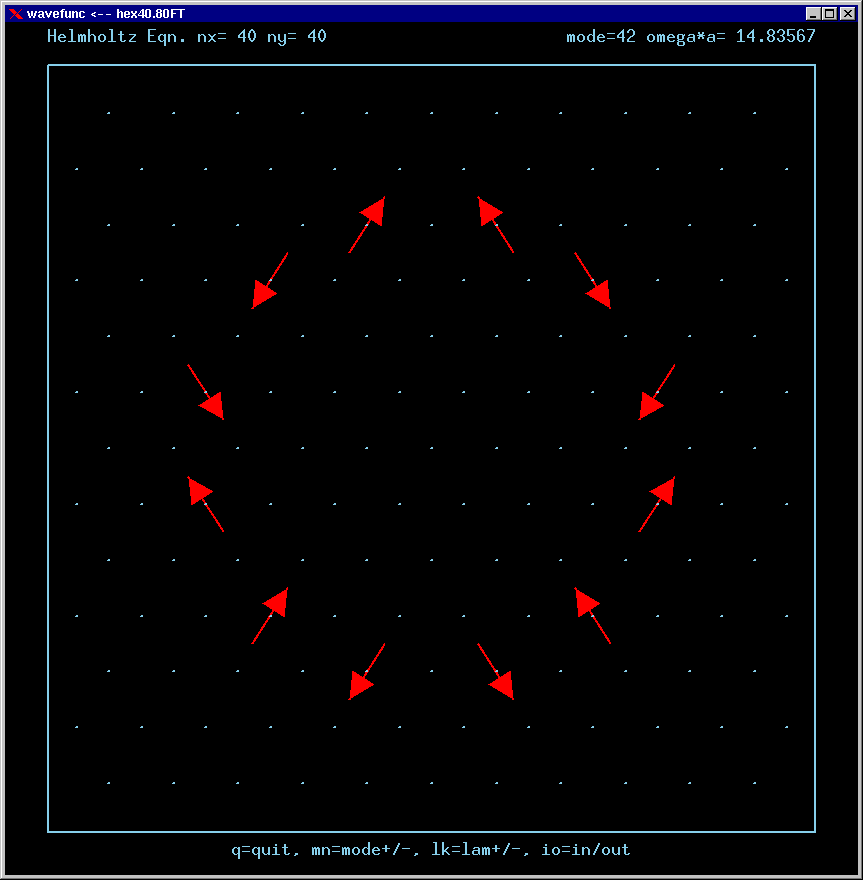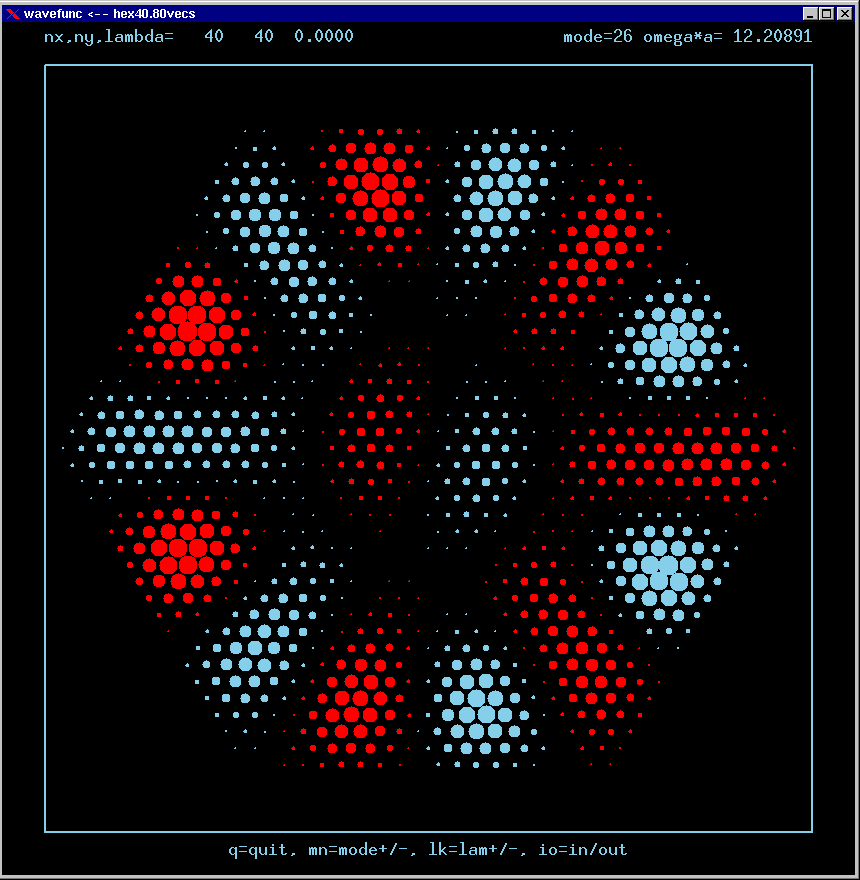
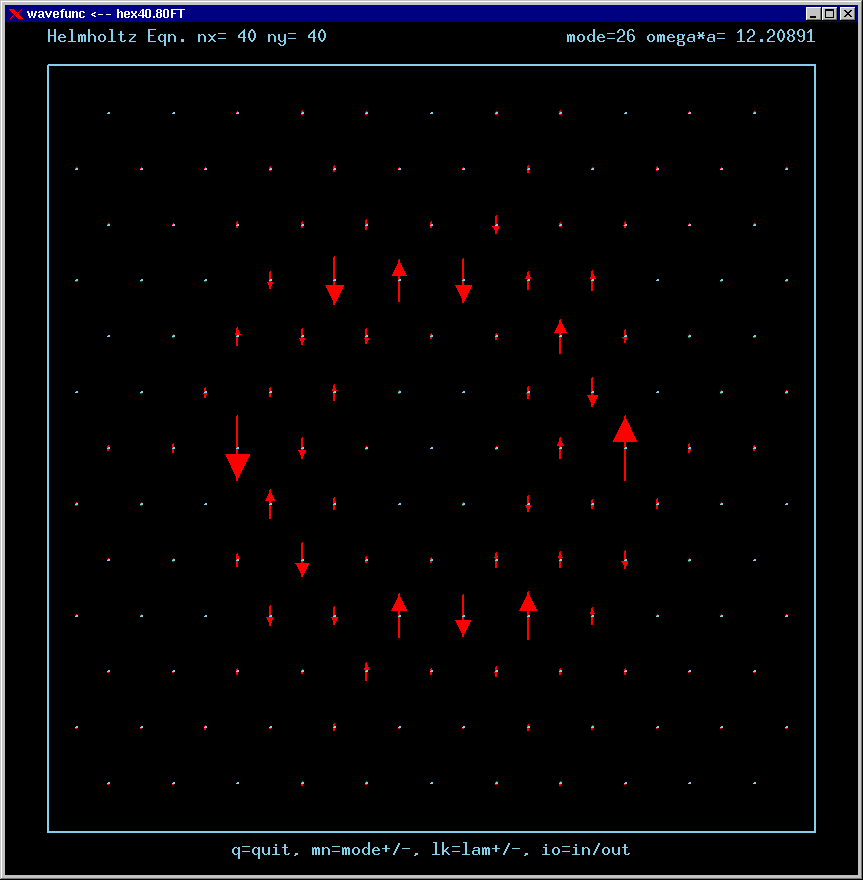
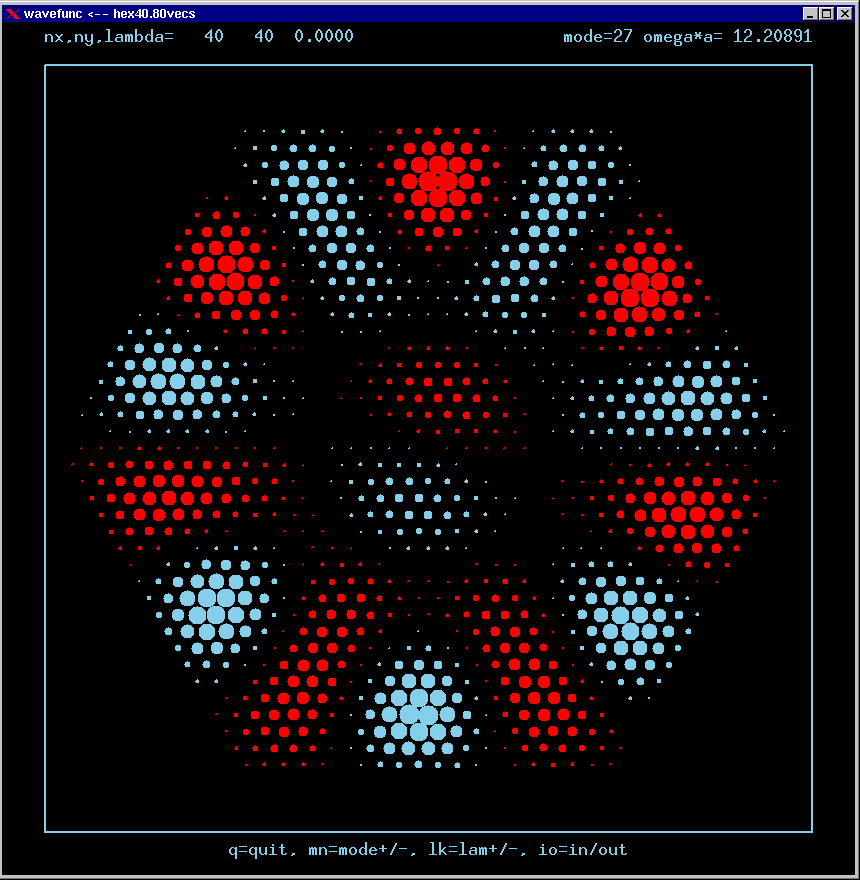
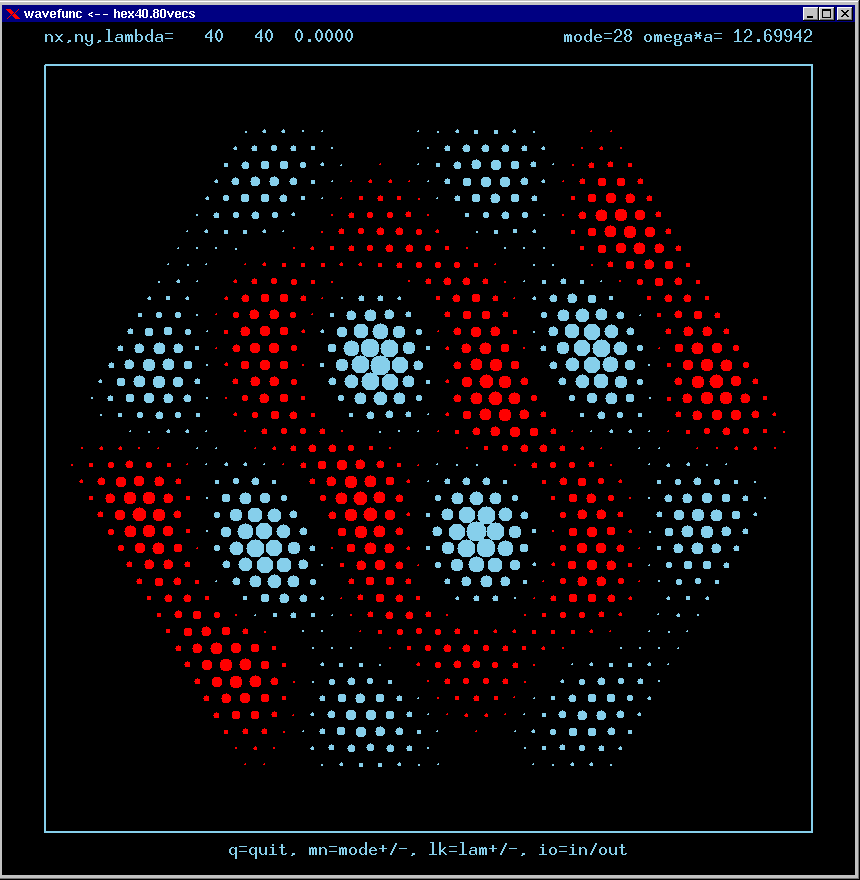
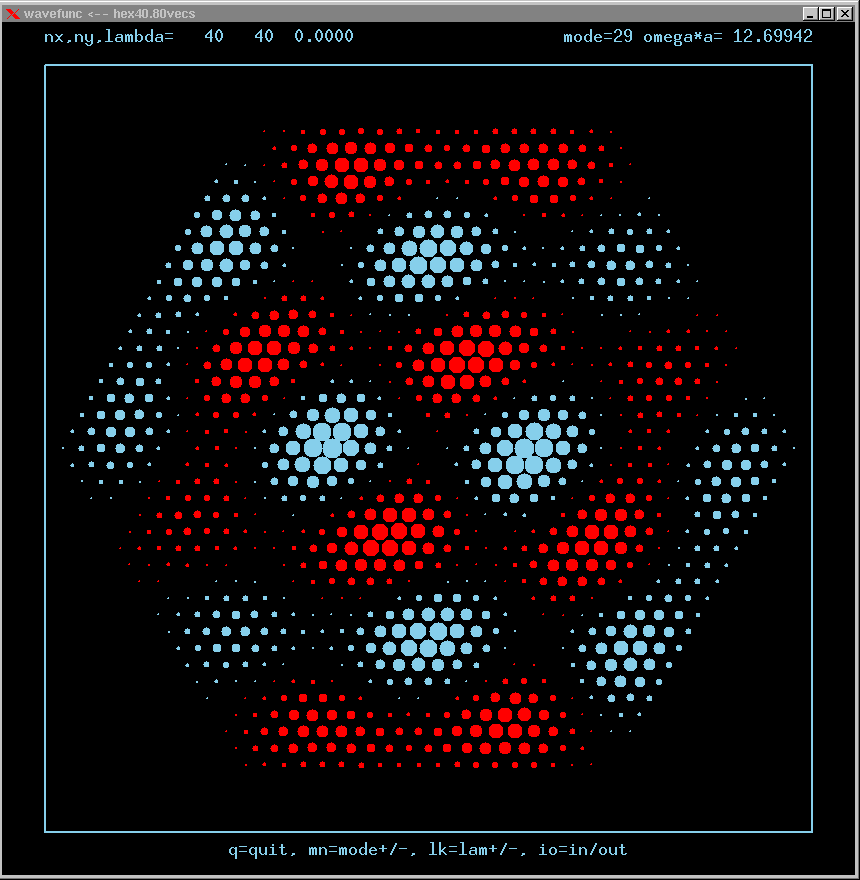
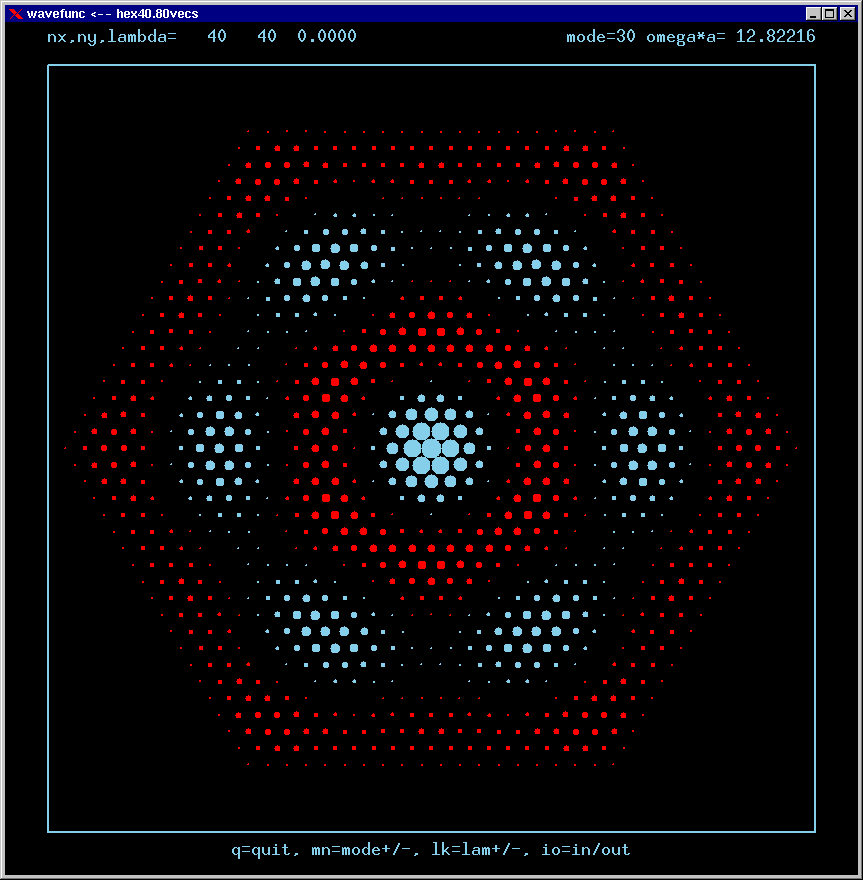
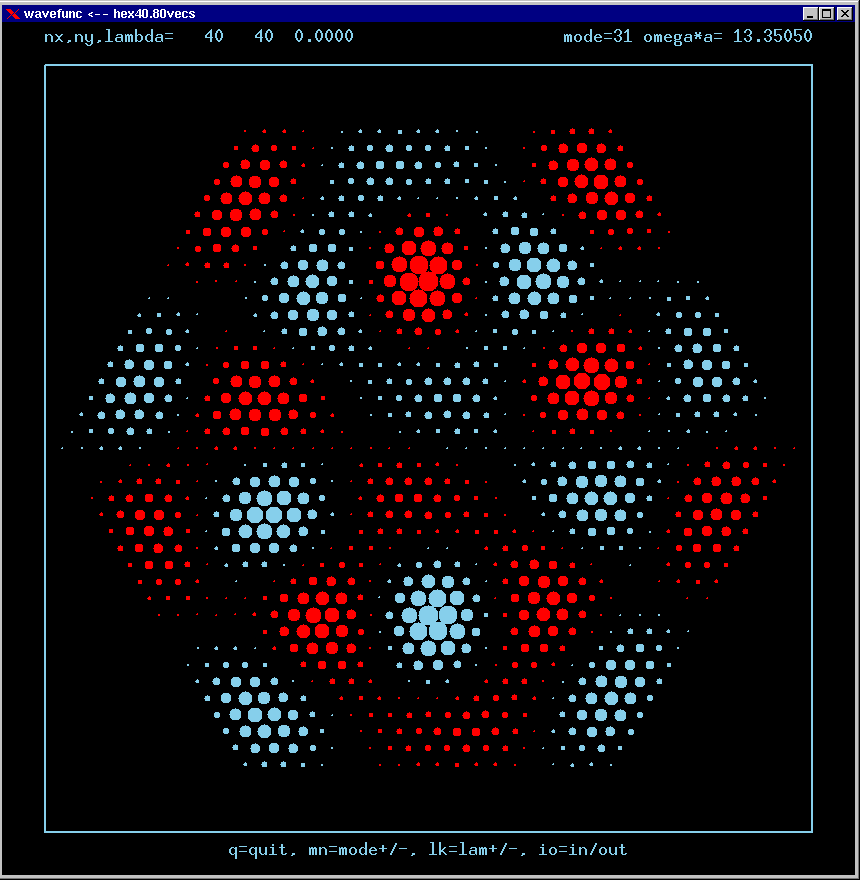
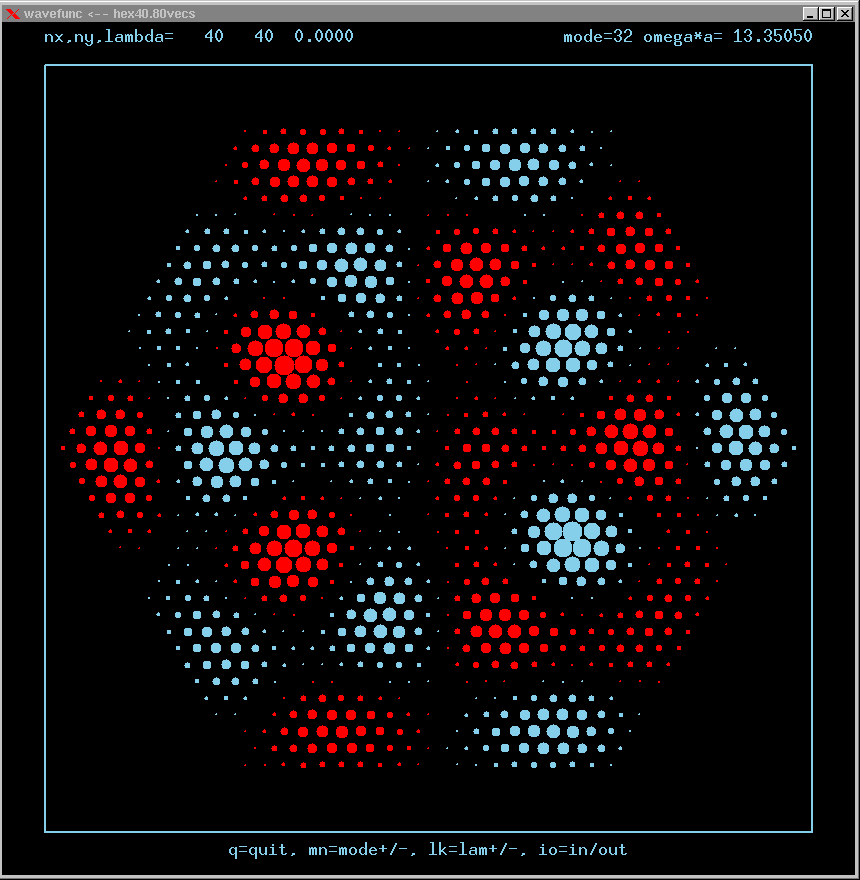
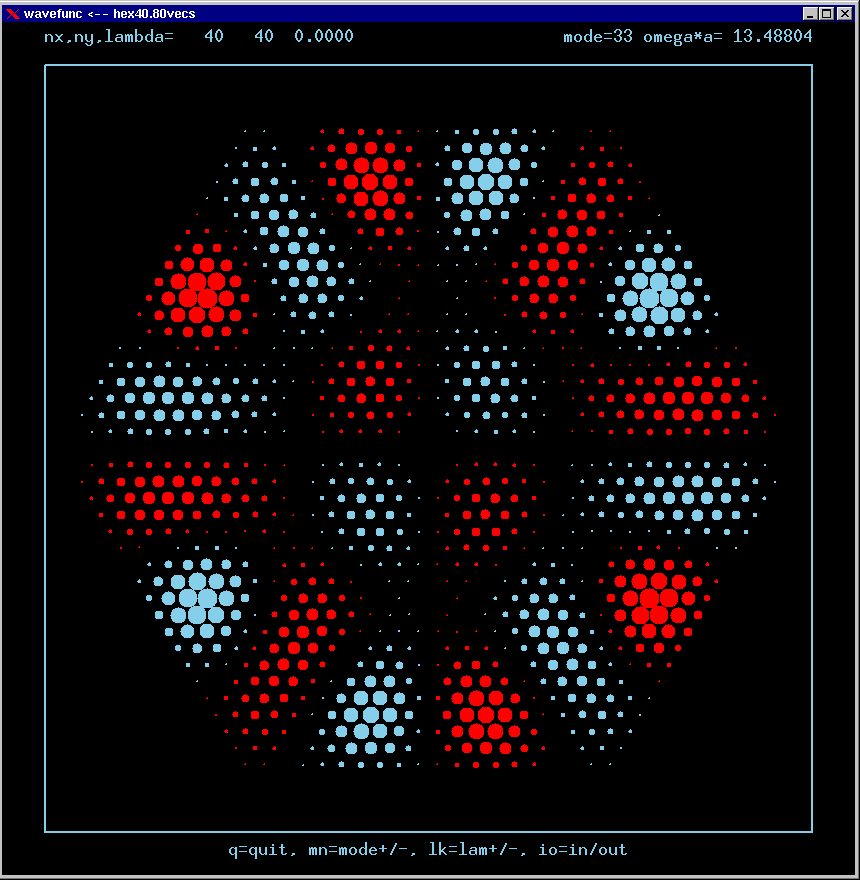
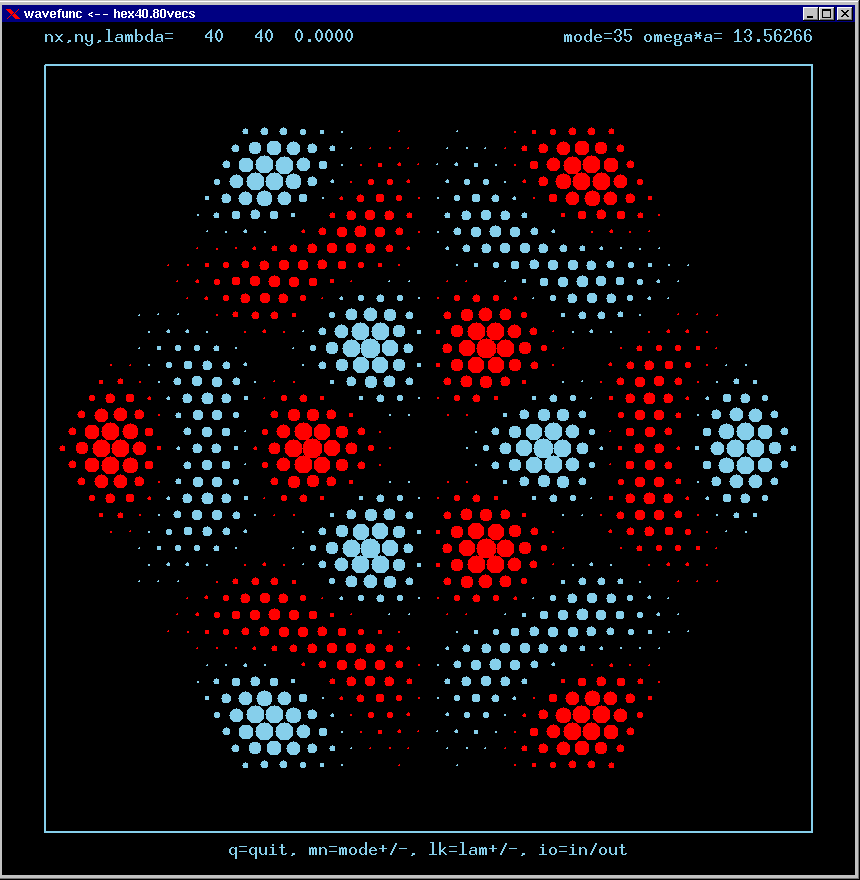
These are the real-valued wavefunctions and complex-valued Fourier Transforms of many of the lowest modes, obtained from a Gauss-Seidel numerical relaxation procedure. They are displayed on a grid for convenience; the wavefunction magnitude at each position is proportional to the symbol size there. Red is positive, blue is negative wavefunction value.
Modes are labelled only by the sequence number in which they were found, starting from the lowest frequency and working upwards in the spectrum. Some modes are single or nondegenerate. Other modes are doubly degenerate (having the same frequency as another independent mode of vibration). Certain modes are simply the analytic repetition of the modes of an equilateral triangular cavity repated over the 6 triangles making up the hexagon!
The dimensionless frequency numbers on the plots are actually omega*a*n/c, where n is the index of refraction inside the cavity, and c is the speed of light in vacuum.
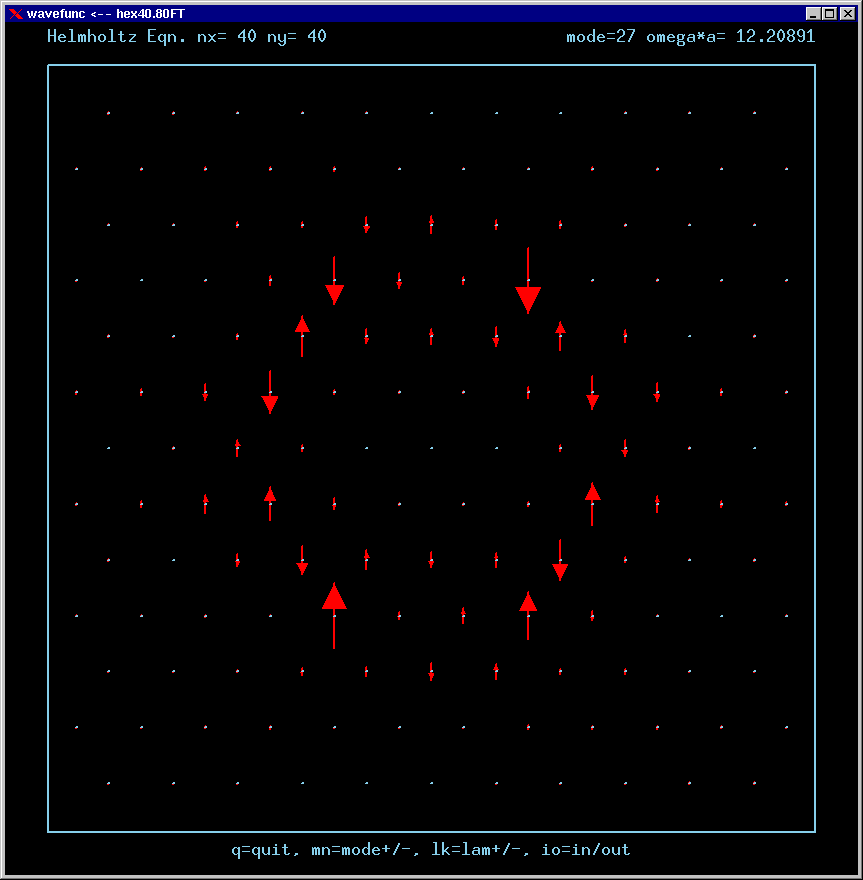
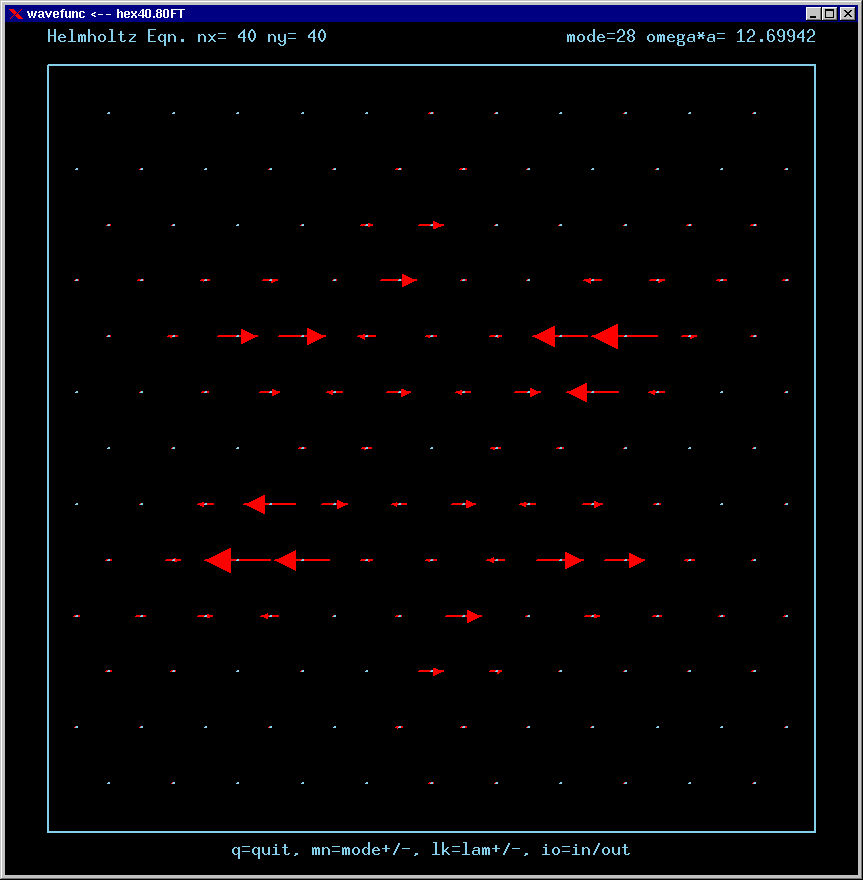
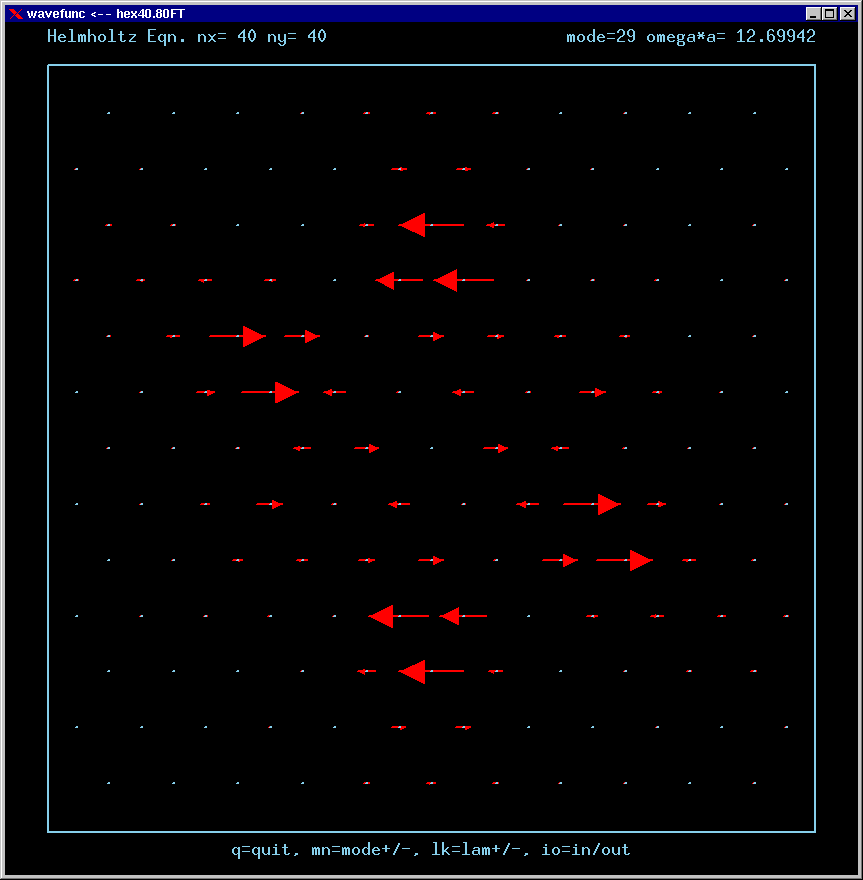
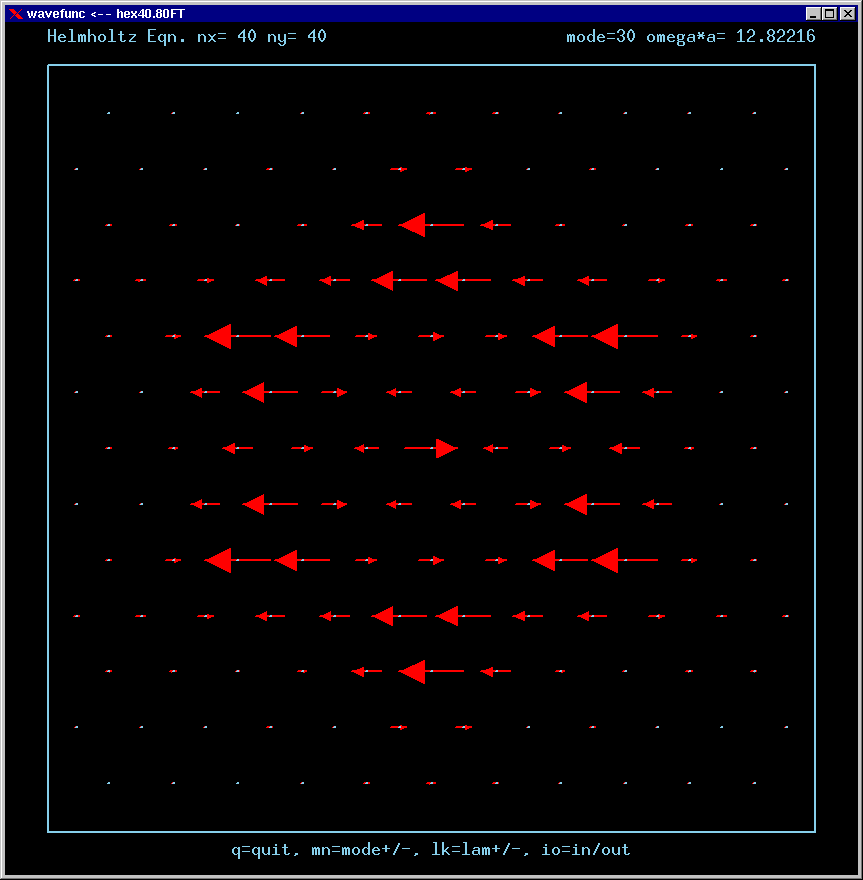
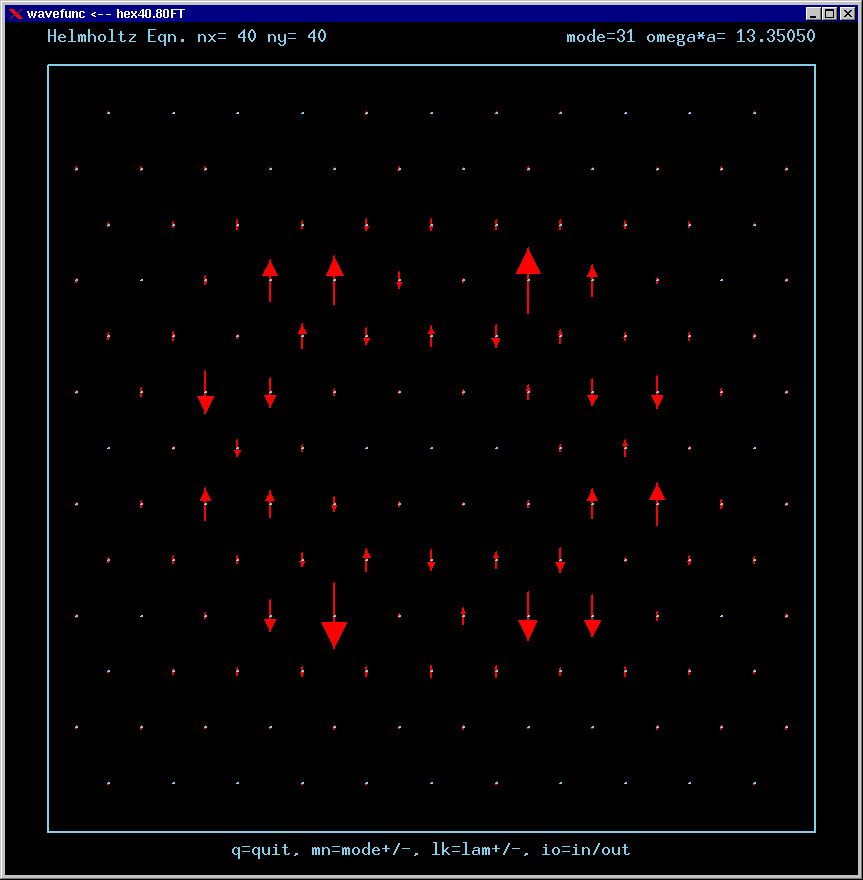
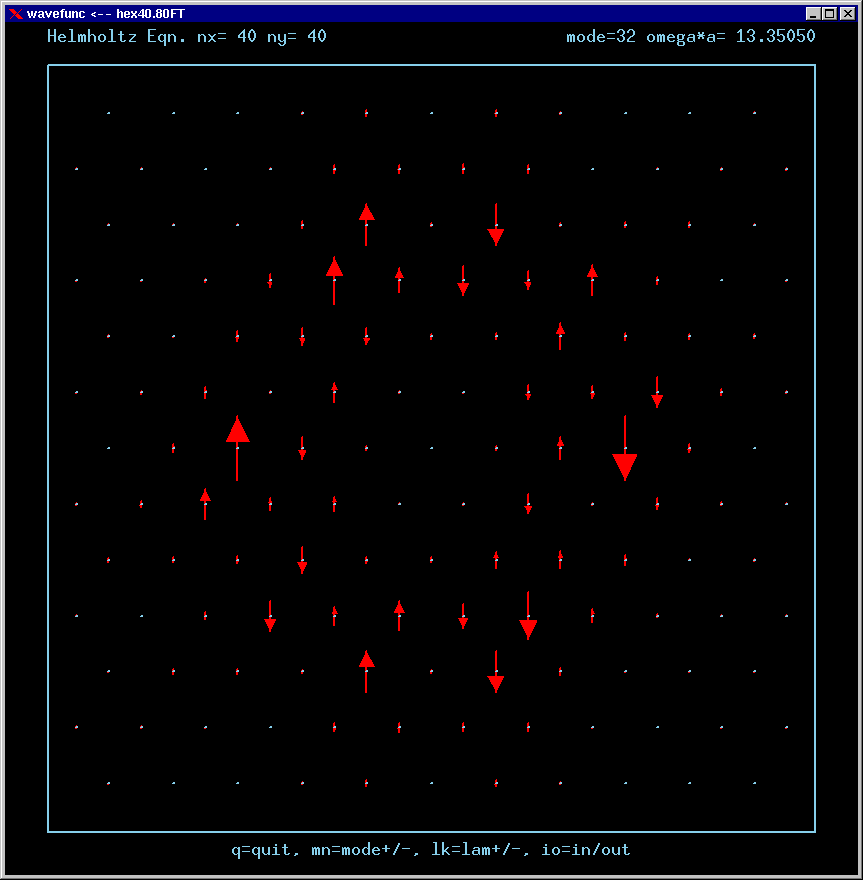
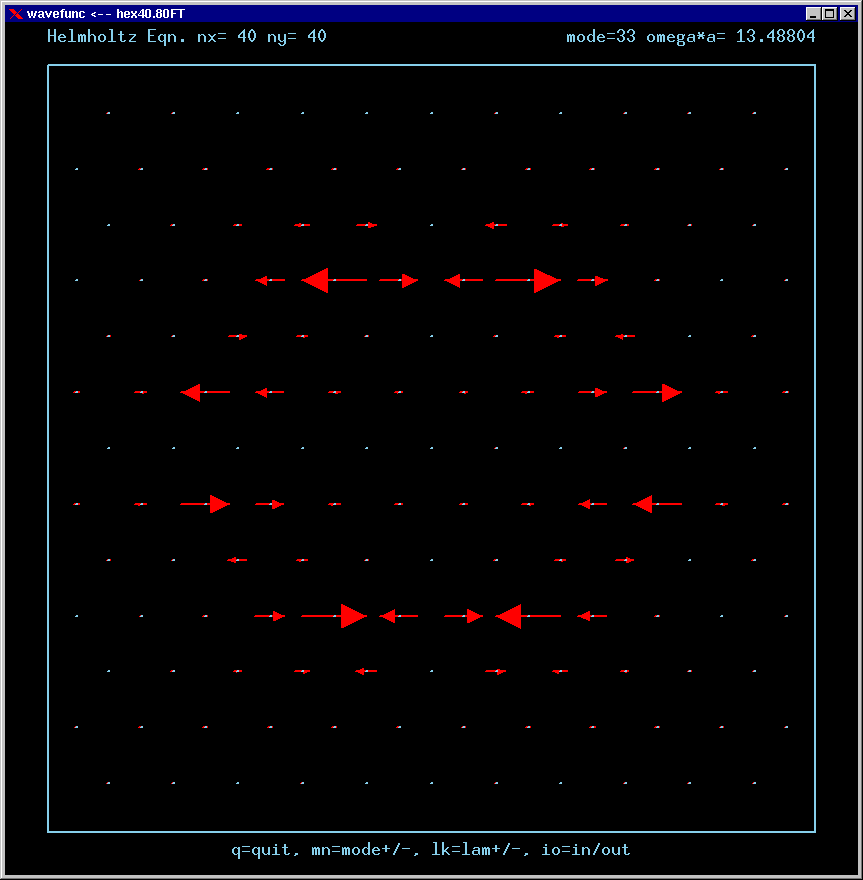
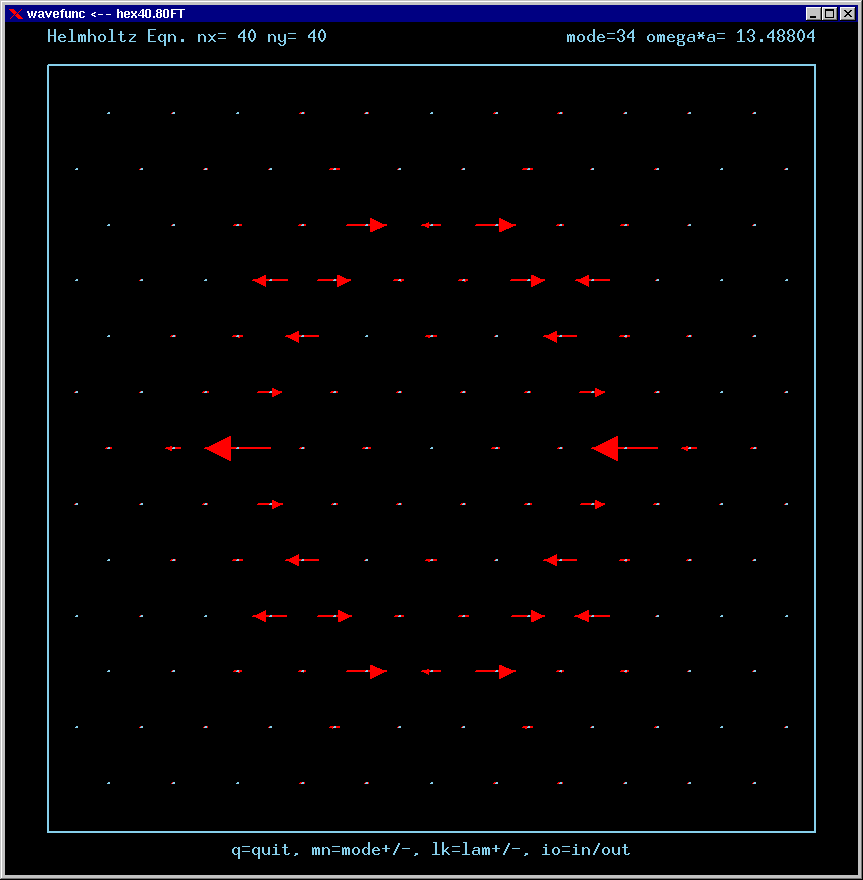
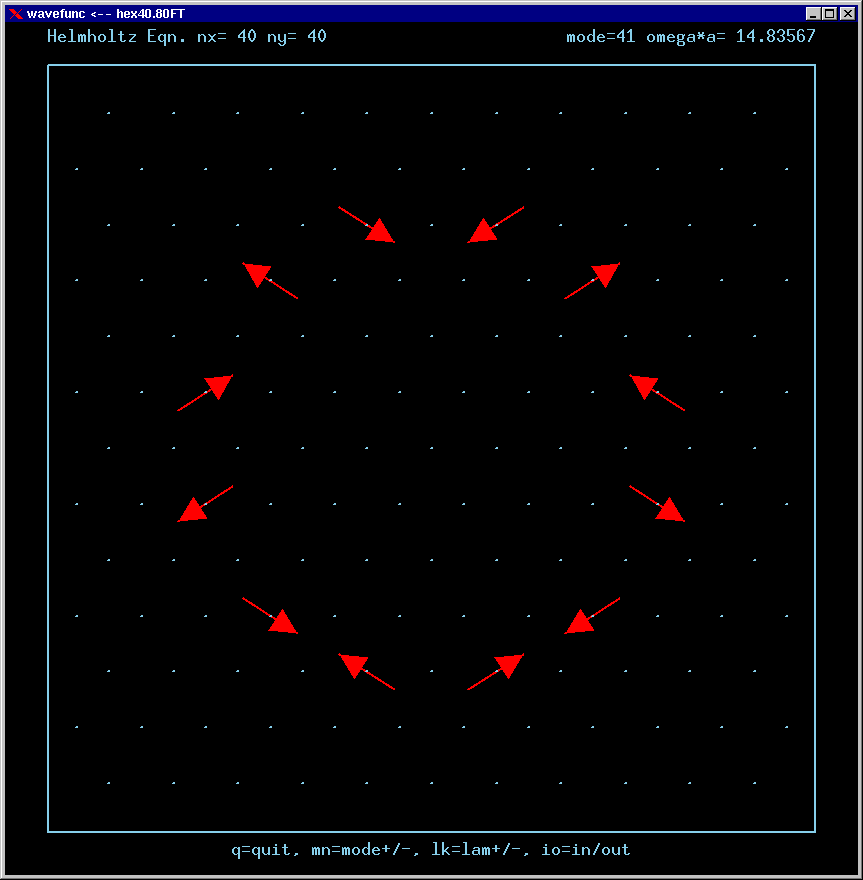
For the Fourier Transforms, the arrows represent the magnitude and phase of the Fourier amplitude at a chosen wavevector. The spacing of the grid points in Fourier space is 4*pi/3a. The entire Brillouin zone is hexagonally shaped. The wavevector (kx,ky)=(0,0) is the point at the center of the diagram. Only the important inner part of the BZ is shown in most of these figures.
A mode can be confined by total internal reflection as long as there is no FT amplitude propagating normal to any boundary. For example, applying this reasoning to the upper horizontal boundary, a mode cannot be confined if there is FT amplitude along the positive vertical axis of the FT diagram.
If a mode has no FT amplitudes anywhere near normal incidence to any boundary, it is called a strong TIR state .
If a mode has no FT amplitudes at normal incidence to the boundaries, but does have amplitudes at arbitrarily small incident angles, then it is called a weak TIR state.
Click image for a postscript file of that figure.
Mode 26 (degenerate with 27) and its FT:


Mode 27 (degenerate with 26) and its FT:
Mode 28 (degenerate with 29) and its FT:
Mode 29 (degenerate with 28) and its FT:
Mode 30 (nondegenerate) and its FT:
Mode 31 (degenerate with 32) and its FT:
Mode 32 (degenerate with 31) and its FT:
Mode 33 (degenerate with 34) and its FT:
Mode 34 (degenerate with 33) and its FT:

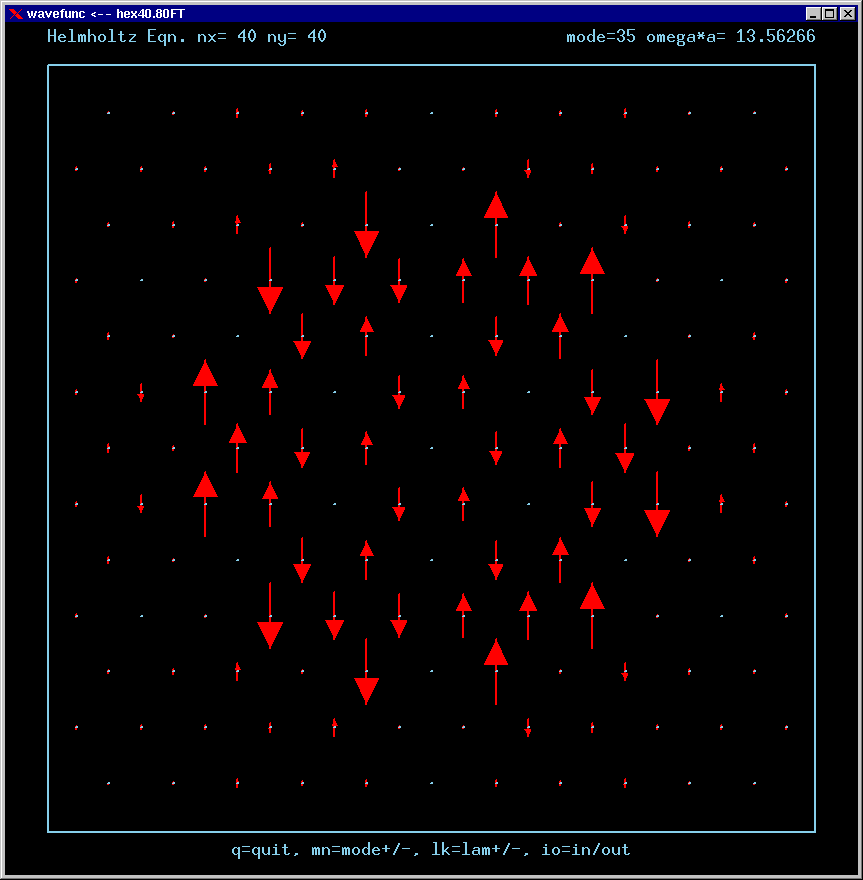
Mode 35 (nondegenerate, weak TIR) and its FT:
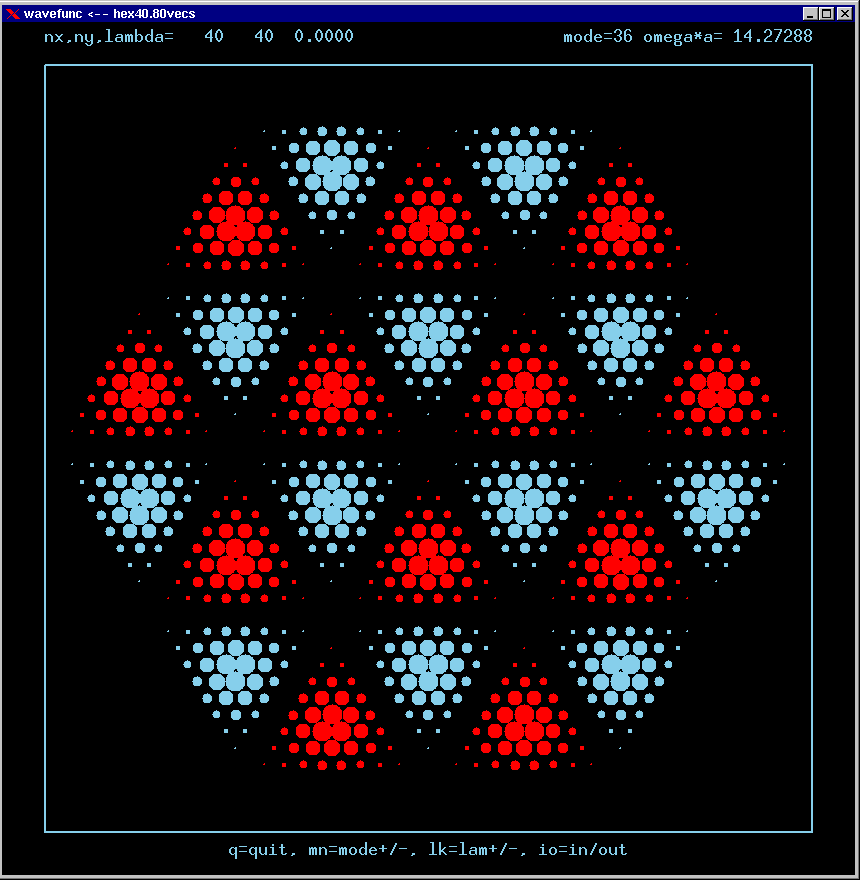
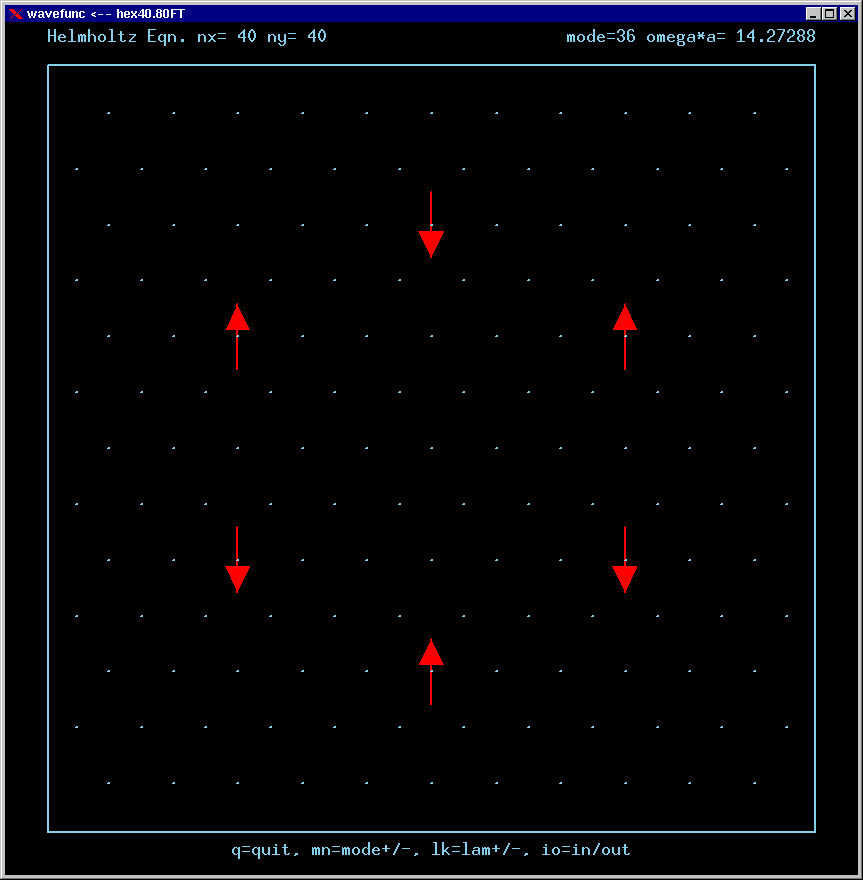
Mode 36 (nondegenerate, m=0, n=4 triangle state, NO TIR) and its FT:
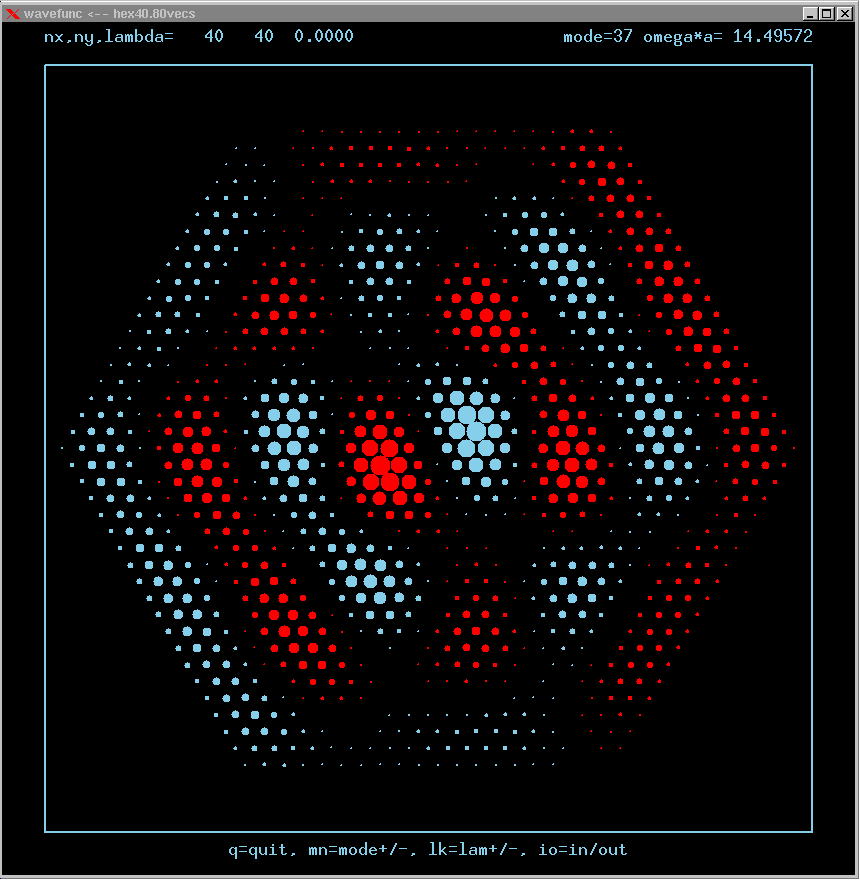
Mode 37 (degenerate with 38) and its FT:
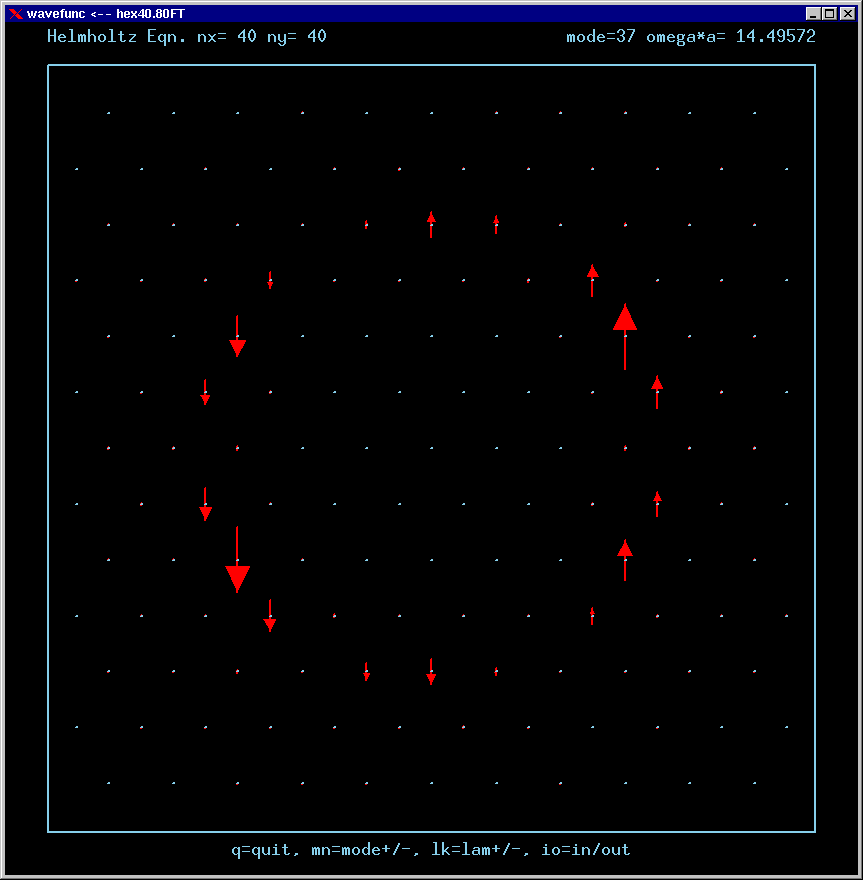
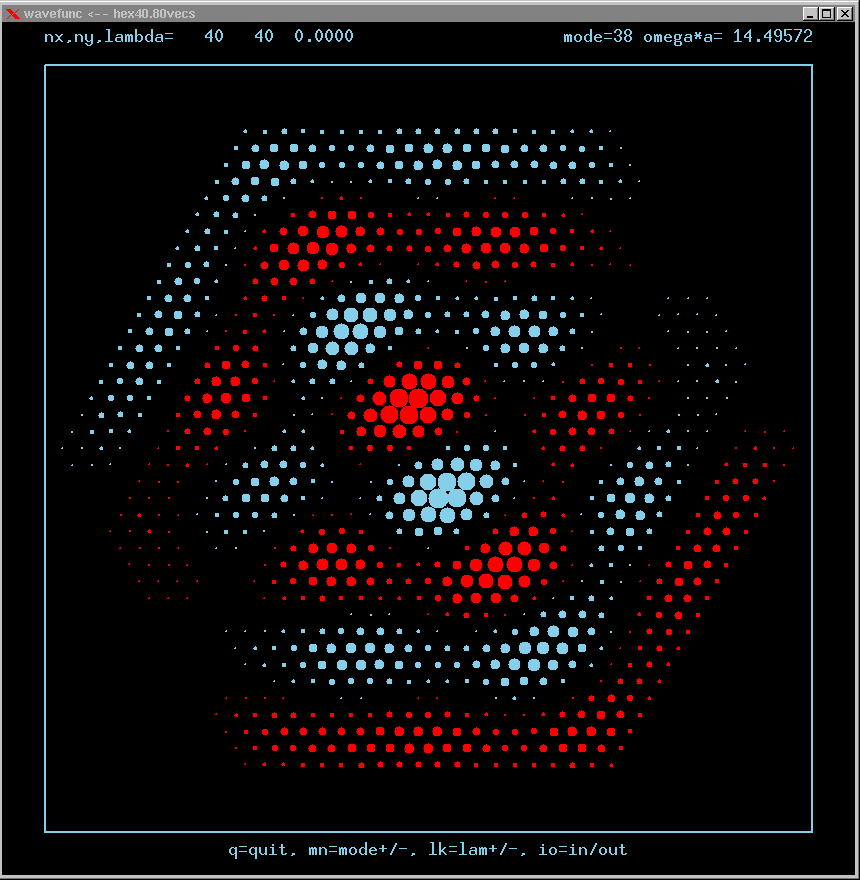
Mode 38 (degenerate with 37) and its FT:
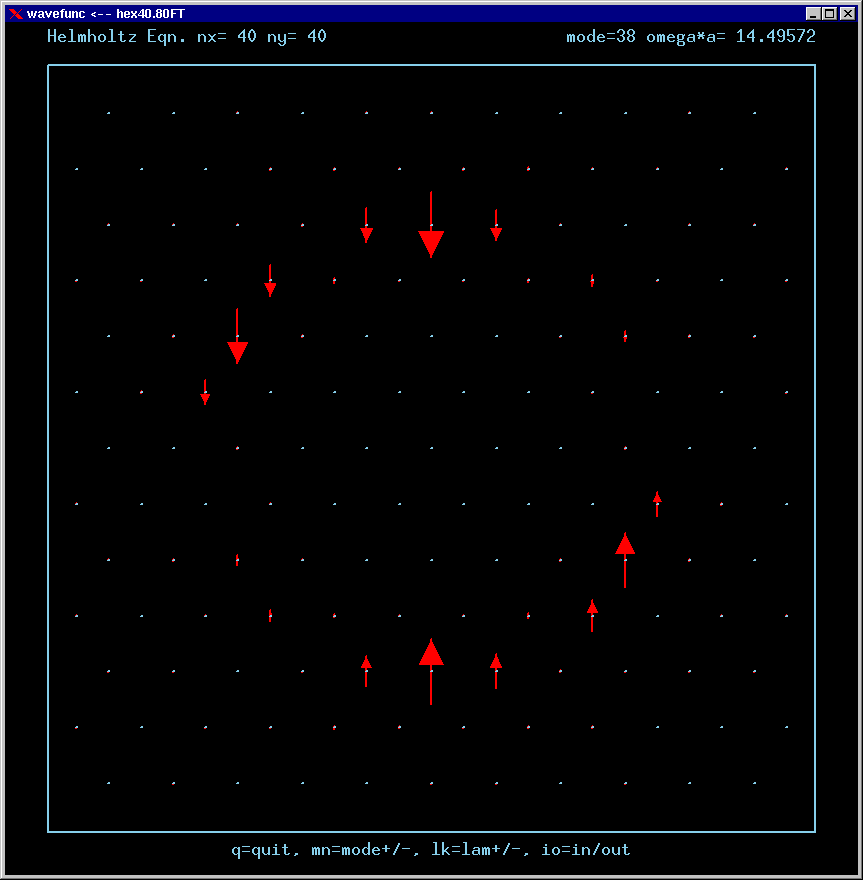
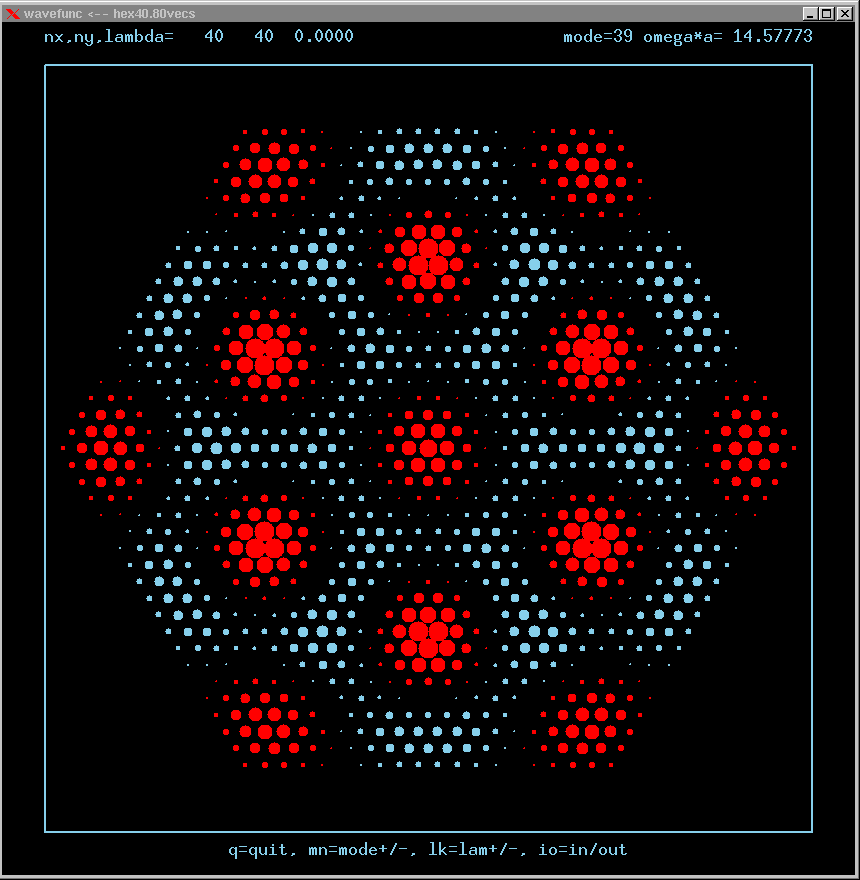
Mode 39 (nondegenerate) and its FT:
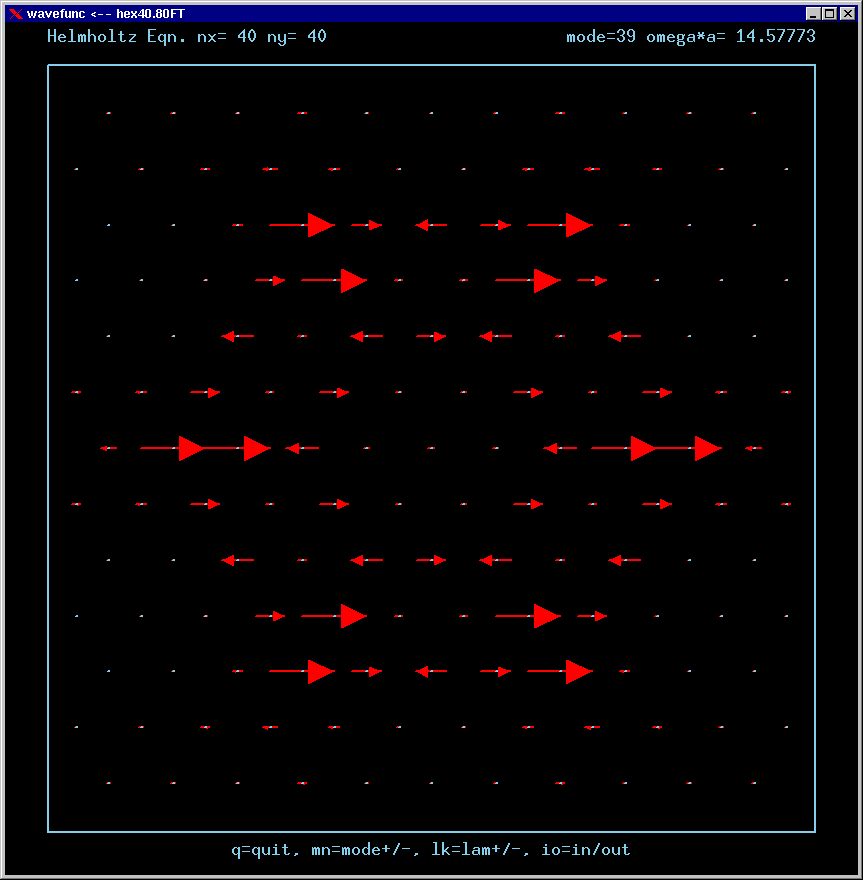
Mode 40 (nondegenerate, weak TIR) and its FT:
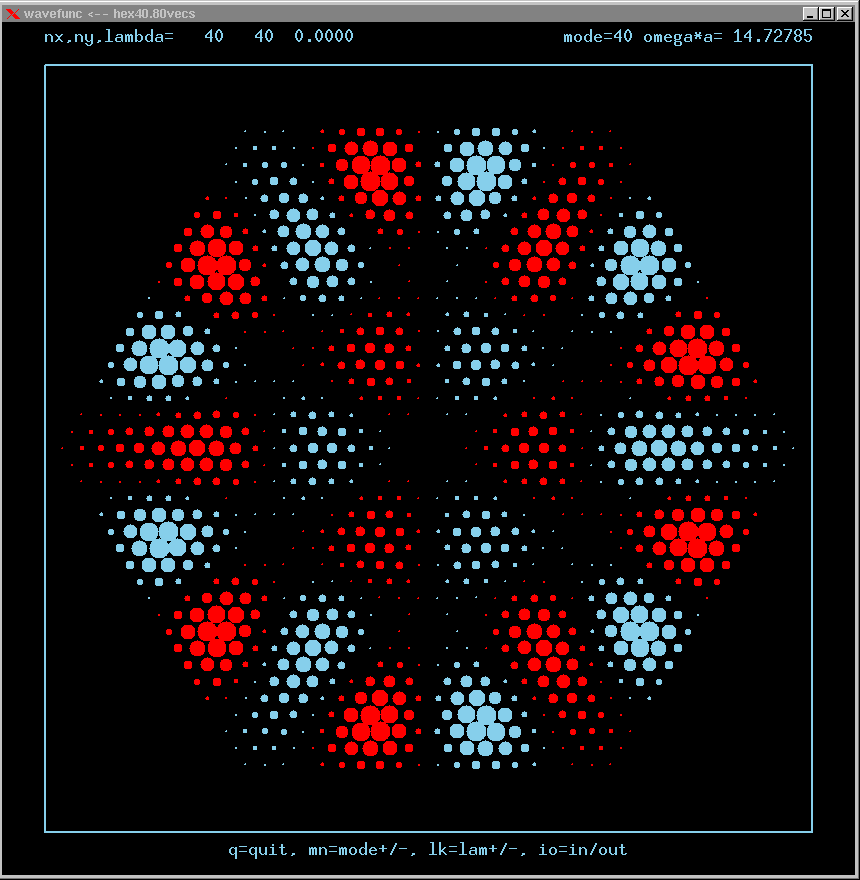
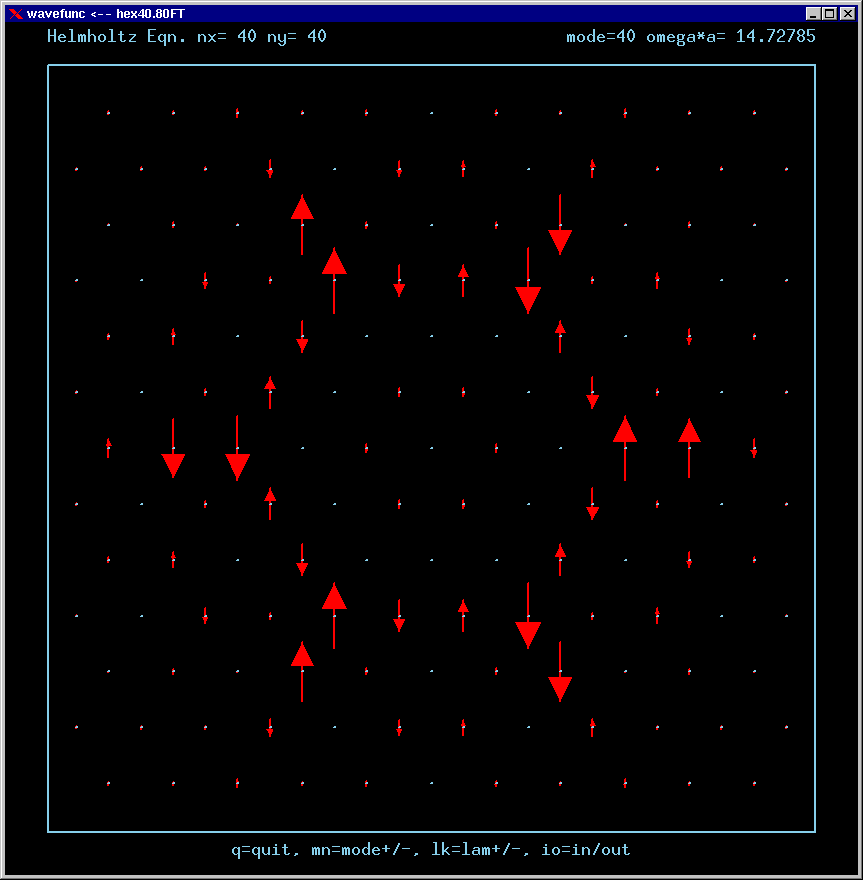
Mode 41 (degenerate with 42, m=2, n=4 triangle state, strong TIR) and its FT:
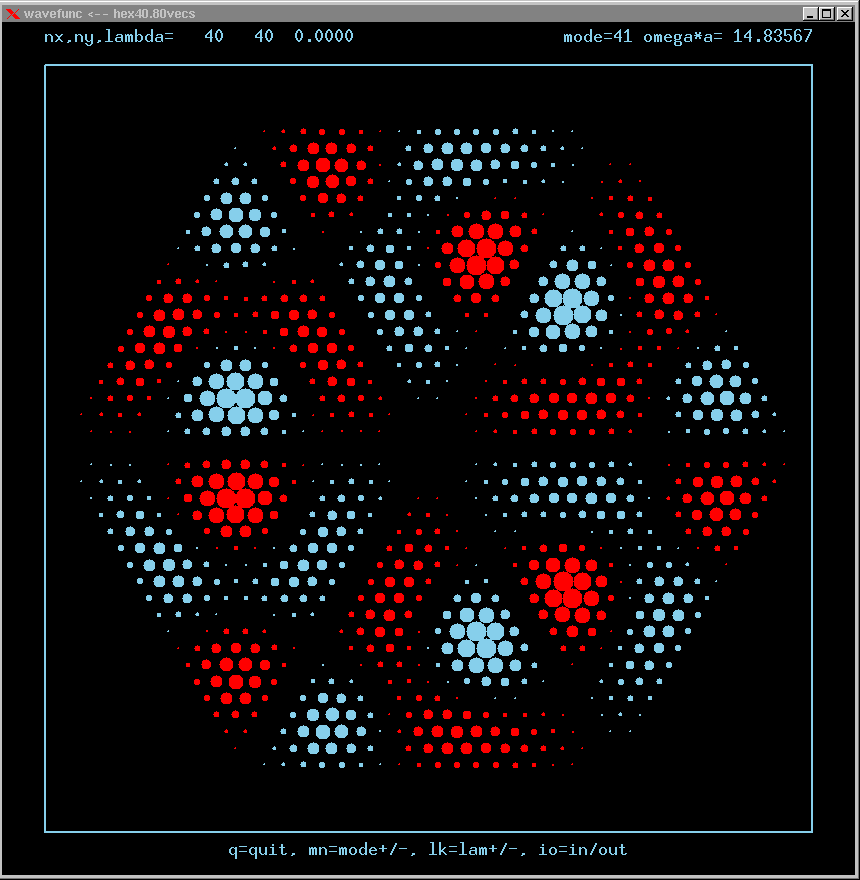
Mode 42 (degenerate with 41, m=2, n=4 triangle state, strong TIR) and its FT: