Class 13.5 (0xD.8): Feldman-Cousins confidence regions

How do we choose confidence intervals (Neyman construction)

(Following section 32.3.2.1 in [PDG-Stat].)

Find intervals for each value of the parameter 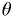$\theta$ such that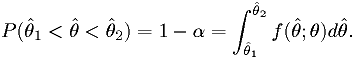

$P(\hat{\theta}_1 < \hat{\theta} < \hat{\theta}_2) = 1-\alpha = \int_{\hat{\theta}_1}^{\hat{\theta}_2} f(\hat{\theta};\theta) d\hat{\theta}.$

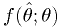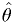Here $f(\hat{\theta};\theta)$ is the p.d.f. of the estimator $\hat{\theta}$ .
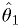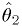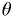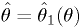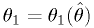$\hat{\theta}_1$ and $\hat{\theta}_2$ should depend on $\theta$ monotonically. The functions are invertible: $\hat{\theta}=\hat{\theta}_1(\theta)$ implies $\theta_1 = \theta_1(\hat{\theta})$ .
Then (see figure)

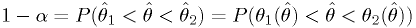
$1-\alpha = P(\hat{\theta}_1 < \hat{\theta} < \hat{\theta}_2) = P(\theta_1(\hat{\theta}) < \hat{\theta} < \theta_2(\hat{\theta}))$

The "Feldman-Cousins" method for generating "unified" confidence intervals

(See section 32.3.2.2 in [PDG-Stat].)

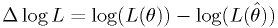We pick the edges of the region to have a particular difference log-likelihood from the best fit point, $\Delta \log L = \log(L(\theta))-\log(L(\hat{\theta}))$ .
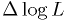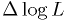The right $\Delta \log L$ to use varies as a function of the best fit parameters. So you need a "map" of the correct $\Delta \log L$ to use when checking whether each value of 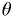$\theta$ should be in or out of the region.
If the parameter space has a boundary, it's no problem, the "map" adjusts the log-likelihood level to encompass enough space.
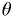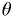Note that the "difference in log-likelihood" is simply the log of the Neyman-Pearson test statistic hypothesis test. The "Feldman-Cousins" technique is equivalent to doing a two-hypothesis test for each possible value of $\theta$ , rejecting points where the hypothesis "the true value is $\theta$ " would be rejected at the $\alpha$ significance level.
In general, the p.d.f. of the log-likelihood is generated via MC for each setting of each parameter, just like the hypothesis test.

The Feldman-Cousins procedure in detail

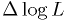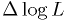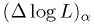The procedure for building up the "map" of $\Delta \log L$ cutoffs is simply to build the p.d.f.s for $\Delta \log L$ on a grid of values of the parameters. For each point on the map, find the value $(\Delta \log L)_{\alpha}$ below which a fraction 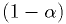$(1-\alpha)$ of the distribution lies.

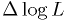Procedure for building up map of $\Delta \log L$ cutoffs for all theta:

Make an array to store the results

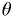Loop over values of $\theta$ :

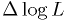build the p.d.f. of  for this parameter (see below)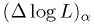
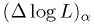sum up the p.d.f. to find the 
store  for this parameter in the array

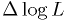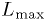The procedure for building up a $\Delta \log L$ p.d.f. is essentially identical to that for building up the p.d.f.s of the $L_\text{max}$ for a significance test, except for the quantity evaluated. (Contrast the steps below to Class 0x0B example 4.)

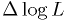Procedure for building up p.d.f. of $\Delta \log L$ :

loop M times:

simulate a dataset using the hypothesis
fit the dataset
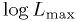calculate  at the best fit point
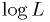calculate  at the true value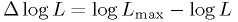
"fill" histogram using 

Procedure for simulating a dataset:

Loop N times:

generate random variable x according to the model p.d.f. for x

(see class notes on MC simulation, use inverse distribution method)

store x in vector of doubles to be used as dataset

(instead of reading x from a file)

Drawing the confidence region

This is simplicity itself:

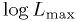given $\log L_\text{max}$ of the best fit point and your map from above,

loop over the points in the "map":

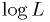evaluate $\log L$ for your real data at that parameter to find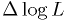 $\Delta \log L$

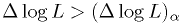is $\Delta \log L > (\Delta \log L)_{\alpha}$ at this point in the map?

if yes, point is excluded -- clear pixel and/or print '.' on screen

if no, point is included -- set pixel and/or print '*' on screen

Exercise/assignment

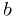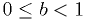Build the 90%-CL and 99%-CL confidence regions for the same exponential + background of the assignment from class 11 (aka class 0x0B), with the restriction that the background parameter must be in the range $0 \leq b < 1$ and the mean 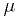$\mu$ must be positive.

Note this is a good example of where the full Feldman-Cousin's treatment is usually necessary: non-Gaussian model, limits on parameters.
Just follow the Feldman-Cousins procedure.
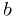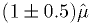Initially, use a grid of 10 divisions from 0 to 1 for , 10 divisions over the range $(1\pm 0.5)\hat{\mu}$ for $\mu$ .
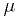Print out the map of 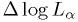$\Delta \log L_\alpha$ to make sure it is reasonable. (Should be 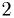for the 90% CL.)
Print out or draw the confidence region.
After getting this to work, make the grid finer if you like.

[KamLAND2008]

KamLAND Collaboration, "Precision Measurement of Neutrino Oscillation Parameters with KamLAND", Phys.Rev.Lett.100:221803,2008; arXiv:0801.4589v3 [hep-ex].

[DZero2010]

D0 Collaboration, "Evidence for an anomalous like-sign dimuon charge asymmetry", Submitted to Phys. Rev. D, 2010; Fermilab-Pub-10/114-E; arXiv:1005.2757v1 [hep-ex].

[PDG-Stat]

"Statistics", G. Cowan, in Review of Particle Physics, C. Amsler et al., PL B667, 1 (2008) and 2009 partial update for the 2010 edition ( http://pdg.lbl.gov/2009/reviews/rpp2009-rev-statistics.pdf ).