Class 9: Fitting data
General problem
We have some model with one or more adjustable parameters 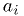 and a
function that describes how well the model fits some set of
measurements. Let's call this goodness-of-fit function
and a
function that describes how well the model fits some set of
measurements. Let's call this goodness-of-fit function 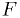 . This
function depends on the parameters of the model, so
. This
function depends on the parameters of the model, so
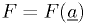 .
.
Our main problem: Find the value of 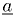 which minimizes
which minimizes 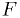 .
This looks like a job for our function minimizer!
.
This looks like a job for our function minimizer!
Secondary task: Estimate how far each 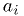 can be perturbed from its
best fit value without increasing the
can be perturbed from its
best fit value without increasing the 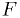 by more than some amount.
This is used for estimating parameter uncertainty ranges or
tolerances. This can be done using the Hessian matrix at the best fit
point.
by more than some amount.
This is used for estimating parameter uncertainty ranges or
tolerances. This can be done using the Hessian matrix at the best fit
point.
Defining the goodness-of-fit function
A common choice for the 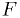 function is the sum of the squares of
normalized deviations of the measurements from the model. For
function is the sum of the squares of
normalized deviations of the measurements from the model. For
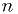 independent measurements
independent measurements 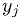 , and corresponding values from
the model
, and corresponding values from
the model 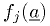 ,
,
![F(\underline{a}) = \chi^2(\underline{a}) = \sum_j \frac{[y_j-f_j(\underline{a})]^2}{s_j^2}.](./imgmath/53d7252a657e10d356029467d987d799.png)
What we choose for 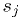 depends on our purpose in fitting the model
to the data.
depends on our purpose in fitting the model
to the data.
- When studying what model best describes the data, we set
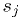 equal
to our best estimate of the RMS error of measurement
equal
to our best estimate of the RMS error of measurement 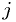 . If the
measurement errors are gaussian and independent, we have a true
. If the
measurement errors are gaussian and independent, we have a true
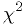 random variable.
random variable. - If we want a function that fits the data for some other purpose, we
choose
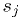 to be appropriate tolerances for that purpose.
to be appropriate tolerances for that purpose.
There are other possibilities for the goodness-of-fit function. (See Other goodness-of-fit functions.)
Example: voltmeter calibration
Situation: for some reason, you have to use an imperfectly calibrated voltmeter. You record the voltmeter readings at several known voltages from a well-calibrated source. You want to be able to convert any reading to the true voltage. You care more about the accuracy in some voltage ranges than in others.
| True voltage | Readout | Readout precision | Required accuracy |
|---|---|---|---|
| 0.000 | 0.000 | 0.001 | <0.001 |
| 0.500 | 0.501 | 0.001 | 0.01 |
| 1.000 | 1.006 | 0.001 | 0.01 |
| 1.500 | 1.512 | 0.001 | 0.003 |
| 3.000 | 3.060 | 0.001 | 0.006 |
| 5.000 | 5.139 | 0.001 | 0.01 |
| 9.000 | 9.450 | 0.001 | 0.01 |
| 12.00 | 12.80 | 0.01 | 0.1 |
| 18.00 | 19.80 | 0.01 | 0.1 |
Voltmeter calibration (continued)
- Your first idea:
- Define the function
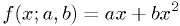 , where
, where  is the reading,
and
is the reading,
and 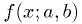 should give the true voltage. Chose
should give the true voltage. Chose 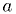 and
and 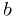 for best fit
of true voltage as a function of readout, using your required accuracy
as the weights
for best fit
of true voltage as a function of readout, using your required accuracy
as the weights 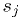 .
. - The voltmeter's designer says:
- The readout voltage
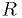 is theoretically a function of the input voltage
is theoretically a function of the input voltage
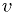 , with
, with 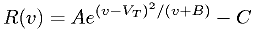 , so you should fit readout
voltage to true value and invert
, so you should fit readout
voltage to true value and invert 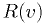 .
.
A statistician agrees, and further says you should use the readout precision, not your required accuracy.
What do you do?
Your voltmeter chi-squared function
Go with your first idea:
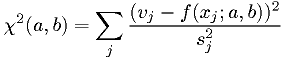
where 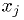 is the readout,
is the readout, 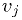 is the voltage, and
is the voltage, and 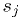 is required
accuracy. Then you will have your useful and easy-to-use function
is required
accuracy. Then you will have your useful and easy-to-use function 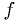 .
.
Now just code that 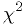 function and run a general-purpose
function minimizer. Start it at
function and run a general-purpose
function minimizer. Start it at 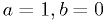 , which is close
to the right solution.
, which is close
to the right solution.
Chi-squared in matrix form
The function
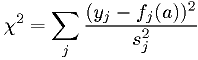
is more generally (in case of correlated measurements)
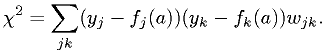
In matrix form,
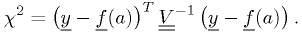
Taking the derivatives with respect to  and setting them
to zero to find the minimum
and setting them
to zero to find the minimum 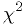 ,
,
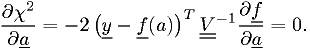
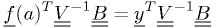
where ![\underline{\underline{B}} \equiv [\partial{f_j}/\partial{a_i}]](./imgmath/32641e8efba72c37e0dbd94c0172d1d6.png) .
.
If we can solve this for 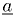 , we're done.
, we're done.
Special case: linear superposition of arbitrary fixed functions
Suppose our model is 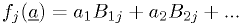 ,
where the
,
where the 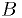 's depend on the measurement index
's depend on the measurement index 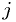 but not on any parameter.
In matrix form,
but not on any parameter.
In matrix form,
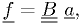
where the 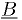 are fixed. Then general problem for the
minimum
are fixed. Then general problem for the
minimum 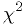 given above becomes simply
given above becomes simply
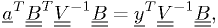
which has the exact solution:
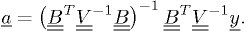
Linearizing the non-linear: voltmeter calibration revisited
The voltmeter fit function from the previous example is just the sum of coefficients times fixed functions, exactly the special case above.
- So we can solve for the best fit using matrix math directly. (There are many C++ packages that provide classes for linear algebra, including ROOT, GSL, Boost, and others.)
- This calculation executes very fast compared to the general function minimization.
N.B. Even though the model for voltmeter was "non-linear", it was a linear superposition of fixed functions. So this is perfect for the "linear fit". This is a commonly occuring case, worth remembering.
Contrast with this case: fit 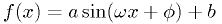 to some
measurements
to some
measurements 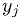 for known
for known 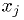 . The
. The 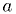 and
and 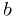 parameters can be
found quickly by the linear fit for given
parameters can be
found quickly by the linear fit for given 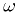 and
and 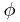 , but
the latter two parameters have to be found by the general minimization
routine.
, but
the latter two parameters have to be found by the general minimization
routine.
Another example: fitting Bode's law
The mean orbital distance 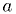 of a planet in the solar system supposedly
fits the relation
of a planet in the solar system supposedly
fits the relation
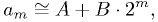
where 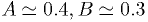 , and
, and
| Planet | m | Observed a (AU) |
|---|---|---|
| Mercury | 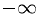 |
0.39 |
| Venus | 0 | 0.72 |
| Earth | 1 | 1.00 |
| Mars | 2 | 1.52 |
| Ceres | 3 | 2.77 |
| Jupiter | 4 | 5.20 |
| Saturn | 5 | 9.54 |
| Uranus | 6 | 19.2 |
| Neptune | 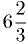 |
30.06 |
| Pluto | 7 | 39.44 |
What are the best 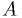 and
and 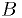 to calculate all planets' mean orbital
distances to the same fractional precision?
to calculate all planets' mean orbital
distances to the same fractional precision?
Assignment: complete fit of Bode's law to planetary data
Feel free to use the minimizer code example from the previous lecture, and just rewrite the function to minimize.
Alternatively, you can base your C++ code on any fitting example from the ROOT website's "howto" or "tutorial" sections.
Alternatively, use the linear fit solution. (But program it, don't just use Matlab or Maple.)
Other goodness-of-fit functions
In other cases, we might use a different function for goodness-of-fit.
Our measurements have non-Gaussian statistics according to our model, and we're really interested in the model or the model parameters themselves:
- Use maximum likelihood method. (Postpone discussion until probability and statistics.)
Our measurements have Gaussian statistics, but there's a correlation between the measurement errors:
There's a straightforward generalization of the
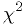 function,
function,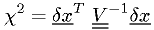
where
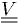 is the covariance matrix.
(Derived from the Gaussian probability distribution.)
is the covariance matrix.
(Derived from the Gaussian probability distribution.)
Our measurements consist of
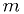 uncorrelated quantities at
uncorrelated quantities at 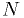 points:
points:- Can be treated just like
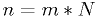 independent measurements.
independent measurements.
- Can be treated just like
Our measurements are similar to the previous case, but our model has a large number
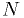 unknown parameters, each of which affects just
the
unknown parameters, each of which affects just
the 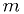 measurements at one of the
measurements at one of the 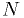 points:
points:- Find a fast way to fit each of the
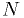 parameters at each point
(ideally from an analytic analysis, such as the linear fit case).
Define the global
parameters at each point
(ideally from an analytic analysis, such as the linear fit case).
Define the global 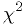 of the remaining parameters, with the
of the remaining parameters, with the 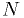 parameter already optimized.
parameter already optimized.
- Find a fast way to fit each of the
There are many other cases, each can be treated by a consideration of the likelihood function and/or the tolerances of your fit for your technical application. Most common cases are covered in the standard references.
References
Press, et al., Numerical Recipes.
G.Cowan, "Statistics", in The Review of Particle Physics, C. Amsler et al. (Particle Data Group), Physics Letters B667, 1 (2008) and 2009 partial update for the 2010 edition. http://pdg.lbl.gov