Class 8: Roots and minima, more C++, and using external libraries
Overview
- Root-finding algorithms in 1-d and multiple dimensions
- Minima-finding algoritms in 1-d and multiple dimensions
- A little more C++: derived classes
- Two examples of external libraries for minimization: GSL and ROOT
Root-finding:
Finding a root of a function (1-d): Solve 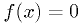 for
for  .
.
- Without using the derivative of
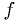 , root can be found by bisection.
, root can be found by bisection. - With the derivative
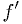 , root can be found using Newton's method.
, root can be found using Newton's method.
Finding root(s) of N functions of N variables: Solve 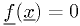 for
for 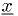 .
.
- Newton's method works here, generalized to N dimensions.
- A related but somewhat different problem: finding N-1 dimensional
contours or surfaces satisfying
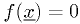 , where
, where 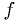 is a
single function, or (N-M)-dimensional contours where M functions are zero.
is a
single function, or (N-M)-dimensional contours where M functions are zero.
- Numerical Recipes describes other algorithms, and gives lots of
- examples and explanations.
Helping the algorithms get the right answer
Give the algorithm a good starting point.
For 1-d root-finders, provide a bracket for the root.
- The bracket is two numbers defining the interval in which to find the root.
- A good bracket
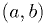 is one in which the function has opposite sign at
the two end:
is one in which the function has opposite sign at
the two end: 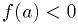 and
and 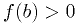 or
or 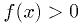 and
and 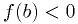 .
.
For the multi-dimensional case, bracketing isn't feasible. The algorithms generally need
- A good starting point
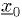 not too far from the root.
not too far from the root. - An initial step size "hint" that is small enough not to overshoot the local minimum, but large enough to see some change in the functions.
Bisection algorithm
Shrink bracket until the root is pinned down, as follows:
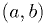 ,
tolerance
,
tolerance 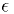 , and function
, and function 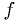 .
.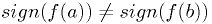 .
.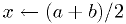
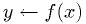
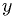 has same sign as
has same sign as 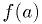 , then
, then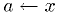
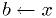
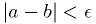
Newton's method
Repeatedly "shoot for the zero," using the approximation
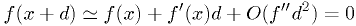
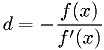
Potential problems can occur when far from the root:
- Big overshoot if
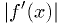 is small.
is small. - Step in wrong direction if
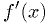 has wrong sign.
has wrong sign. - Non-converging loop if
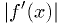 gets shallower farther from the root.
gets shallower farther from the root.
(... Draw figures on board, insert in notes later ...)
Simple Newton's algorithm
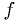 and
and 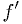 functions, initial
functions, initial  , and
tolerance
, and
tolerance 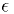 .
.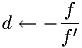
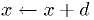
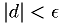 .
.Important note: 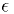 should be small enough for your application,
but no smaller. Make sure it is large enough that
should be small enough for your application,
but no smaller. Make sure it is large enough that 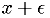 is
different from
is
different from  in your machine's floating point representation.
in your machine's floating point representation.
Smarter Newton's algorithm
Use bracketing to protect against any craziness, bisect whenever a Newton's method step fails.
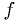 and
and 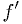 functions, bracket
functions, bracket 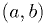 , and
tolerance
, and
tolerance 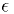 .
.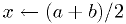 .
.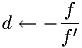
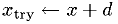
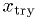 in range
in range 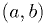 ?
?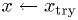
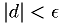 .
.See full example in Numerical Recipes (sec 9.4 in 2nd or 3rd ed.).
Multidimensional case
We have 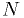 functions
functions 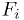 of
of 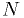 variables
variables 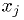 , and want to find the zeros.
, and want to find the zeros.
There's a great illustration in Numerical Recipes showing why this is hard in general. (Fig. 9.6.1.) If you want to seek the nearest zero to some point, Newton's method should work.
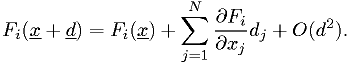
In matrix notation,
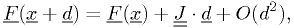
using the Jacobian matrix
![\underline{\underline{J}} =\left[ J_{ij} \right] \equiv \left[ \frac{\partial F_i}{\partial x_j} \right].](./imgmath/72180bcde7ea27fc1998b8728ea19245.png)
To find the root, repeatedly solve
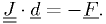
Update 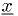 until convergence
until convergence 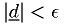 .
.
- Numerical Recipes describes a method for "backtracking" if a
- multi-dimensional Newton's method step makes things worse instead of better.
Minimization
Finding a local minimum: find value for which 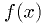 or
or
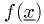 is locally minimized. (To find maxima, just
minimize
is locally minimized. (To find maxima, just
minimize 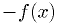 .)
.)
I will describe one particularly pretty 1-d minimization algorithm that requires no calculation of derivatives and that is guaranteed to find a local minimum.
There are faster algorithms that use derivatives, for 1-d and multi-d problems, including ones that only need the user-supplied function. (These algorithms estimate the derivatives themselves.)
I'll describe the general properties of these, and then we will talk about how to use pre-written implementations.
Golden section search
Similar to bisection, except it starts with a triplet of values 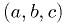 such that
such that 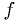 at the middle point is less than at the two ends:
at the middle point is less than at the two ends:
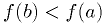 and
and 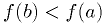 .
.
(... figure ...)
General outline of algorithm:
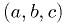 , function
, function 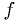 , and tolerance
, and tolerance 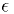
 and try it (*).
and try it (*).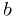 as edge of bracket
as edge of bracket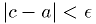 .
.(*) The point  is chosen in the range
is chosen in the range 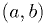 or
or 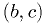 such that
the updated triplet will have the same proportions as the original triplet.
The ideal ratio turns out to be the golden mean.
such that
the updated triplet will have the same proportions as the original triplet.
The ideal ratio turns out to be the golden mean.
More general minimization
Near minimum, to 2nd order,
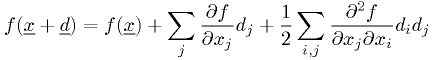
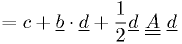
Terminology: The matrix 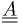 is called the Hessian.
The vector
is called the Hessian.
The vector 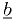 is the gradient.
is the gradient.
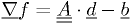
At an extremum, 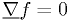 . So we just solve
. So we just solve
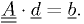
Essentially the same algorithm as Newton's method works if we know
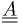 and
and 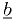 well enough.
well enough.
Types of minimization algorithms
Various algorithms differ in how they guard against crazy steps and whether they need the caller to provide a function for the derivatives or Hessian.
- If we have functions for the 2nd derivatives (
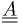 ) and
1st derivatives, we can use an algorithm that uses them.
) and
1st derivatives, we can use an algorithm that uses them. - If we have just the first derivatives, we need an algorithm that estimates the Hessian using the derivatives.
- If we have only the function, we need an algorithm that estimates both the derivatives and the Hessian using finite differences.
What's common among the algorithms:
- All algorithms ultimately seek
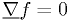 .
. - All need an initial starting point
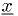 not too far from the
minimum being sought.
not too far from the
minimum being sought. - A step size parameter tells the algorithm what steps are reasonable for doing finite differencing and making the first few trial steps.
Numerical Recipes has many different algorithms.
More importantly, there are existing libraries for minimization of functions.
Break
A little more C++: derived classes
C++ lets you define a new class based on an existing class, like this:
class NewClass : public BaseClass {
// usual class definition
};
This defines NewClass as having all the same data and member functions as BaseClass, with the following enhancements:
- Add any new data members defined in NewClass.
- Add any new function members declared in NewClass.
- If a virtual function member declared in BaseClass is redeclared in NewClass, the hidden virtual function pointer point to the new function for NewClass objects.
- If you start the definition with class NewClass : private BaseClass, then the base class functions will be made private in the derived class, even if they were public in BaseClass.
This is not impossible in C, just clunky
| C++ | C |
class MyBase {
int i;
public:
virtual void set_i(int ii);
};
class MyClass2 : public MyBase {
int j;
public:
virtual void set_i(int ii);
virtual void set_j(int jj);
};
|
struct MyBase_s {
int i;
void (*set_i)(int ii);
};
struct MyClass2_s {
strict MyBase_s base;
int j;
void (*set_j)(int jj);
};
|
| C++ constructor sets virtual function table for new MyClass2 object's set_i and set_j to the correct addresses for MyClass2::set_i() and MyClass2::set_j(). | For any new MyClass2_s variable made, C programmer has to set the values of .set_j and .base.set_i pointers to point to the right functions, and i field must be accessed as base.i. |
Example of minimizer in C using object-oriented approach: GSL
See very nice documentation in GNU Scientific Library Reference Manual, section titled "Multidimensional Minimization". http://www.gnu.org/software/gsl/manual/html_node/Multidimensional-Minimization.html
Things to note about how they write documentation:
- The especially nice write-up of the problem being solved and the algorithm properties.
- The especially nice write-up of how to use the functions.
- The really useful examples subsection.
Things to note about the API:
- It's C, but object oriented, using pointers to structs and functions.
Example of a minimizer in C++: ROOT
The best documentation from the authors is at http://root.cern.ch/root/html526/TMinuitMinimizer.html
- It's very detailed at the low level, and has some high level overview.
- However, there are some critical things missing at the middle level,
such as a clear statement of how to make it actually start minimizing.
- It turns out one of the 49 functions defined for the class is named Minimize(), and that's the one to make it go, after setting up using SetFunction() and SetVariable().
- On their website, I found lots of examples of fitting, but none of
pure minimization, so I wrote one for you. (See link
in course web page.)
- The example finds the minimum of the function
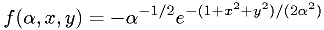 .
.
- The example finds the minimum of the function
Assignment (easy?)
Get the ROOT examples from the course web page to compile and run.