Class 6: Numeric ODE integrators; API design and testing
The basic n-dimensional ODE equation
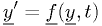
where 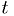 is the independent variable,
is the independent variable, 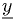 are the dependent variable, and underlines denote vectors.
are the dependent variable, and underlines denote vectors.
This looks like a first-order ODE, but it can represent a higher
order ODE with a simple "chain" of variables. E.g.,
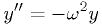 can be implemented by defining
can be implemented by defining 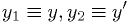 , and
, and
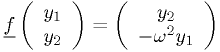
We can also eliminate explicit 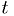 dependence by making it one of the
elements of
dependence by making it one of the
elements of 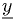 .
.
Note: I'm going to drop the underlines now, but 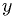 and
and 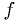 are still vectors.
are still vectors.
Numerical solutions
- We want to find approximate numeric solutions of some accuracy without already knowing the analytic solution.
- For initial value problems, we do this by integrating the ODE in
discrete steps in
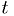 . The step size is conventionally called
. The step size is conventionally called 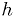 .
. - The easiest starting point is the Taylor series.
Euler 1st order:
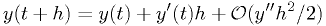
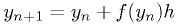
2nd order
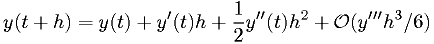
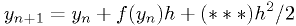
*** If we require that only the function 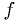 be specified
in analytic form, not its derivatives, then
be specified
in analytic form, not its derivatives, then 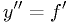 has to be estimated from
previous or future values of
has to be estimated from
previous or future values of 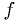 in some clever way.
in some clever way.
Heun's method: 2nd order
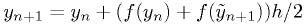
where 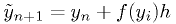 is the
Euler's method approximation for
is the
Euler's method approximation for 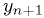 .
.
This is equivalent to
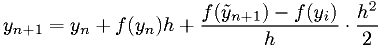
Fourth-order Runge-Kutta
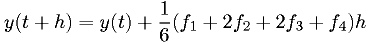
where
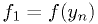
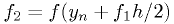
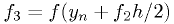
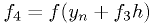
Programming for reusability
General principles:
- Don't embed an algorithm everywhere you need it. That forces you to rewrite it repeatedly.
- Write once, reuse often!
- This is a little more work, but usually pays for itself quickly.
- The little bit more work: you have to design an API for your algorithm.
An API for an ODE solver
The API can be very simple: just one function to advance one step.
The ODE step function takes three arguments:
- The starting value of
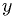 . (A vector<double>.)
. (A vector<double>.) - The function for
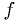 . (A pointer to a function.)
. (A pointer to a function.) - The size of the step
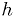 .
.
There are two options for how to return the updated value:
- Actually return the new value.
- Update the existing
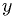 "in place" (pass by reference).
"in place" (pass by reference).
The 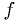 function takes a little more thought.
function takes a little more thought.
How to define the derivative function?
The straight-forward way: pass-by-value, return a value:
vector <double> f( vector<double> y );
Pass-by-reference (in and out):
void f(const vector<double> &y, vector<double> &f_out);
The second way is up to a factor of 2 faster because it requires less copying of data between memory locations.
API to use in today's assignment
typedef void f_vect_vect_t(const vector<double> &y,
vector<double> &f_out);
void rk4step(vector<double> &y,
f_vect_vect_t * fptr,
double h);
A note on "name space"
Good "namespace" citizenship:
- Choose names unlikely to be used elsewhere. (E.g., "f" would be a bad name for a globally-defined function or type.)
- C++ namespaces were designed to help with this.
Testing
- Write test cases for your functions.
- You need a test independent from your main application!
- Don't be fooled into thinking you can always recognize a wrong answer when you see it. If you already knew the answer to your main problem, you wouldn't be writing this program in the first place.
Test case: oscillators and orbits
We know the solutions to 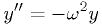 and to
and to
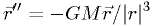 .
Let's test the Euler ODE solver with that case.
.
Let's test the Euler ODE solver with that case.
Code: see course web page.
Results of test
Position vs time:
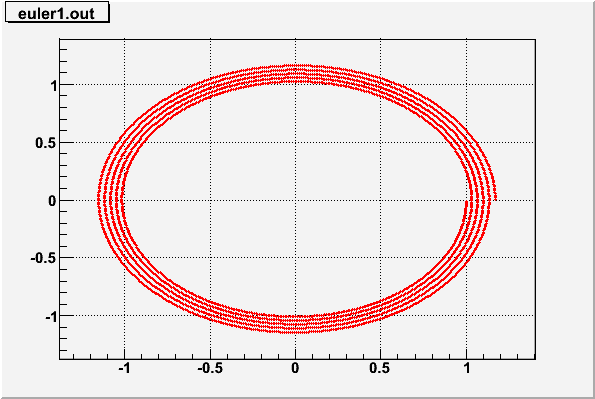
Results of the test program for Euler integration of the simple harmonic oscillator equation. Note how points spiral out.
It's spiralling outward. Energy is not being conserved!
What went wrong?
Momentarily using the underline notation again, the vector
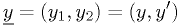 is a vector in phase space.
It is supposed to follow a closed path, but the finite steps in the
1-st order Euler ODE solver don't allow that.
is a vector in phase space.
It is supposed to follow a closed path, but the finite steps in the
1-st order Euler ODE solver don't allow that.
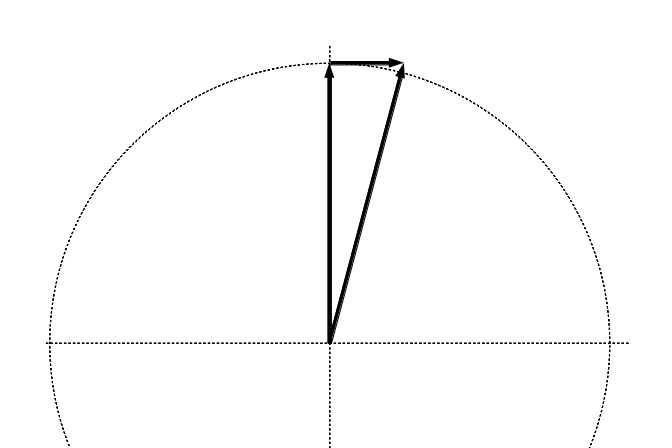
Addition of a finite correction perpendicular to a vector.
Symplectic ODEs
The harmonic oscillator and orbit problems, and many others in science in engineering, are examples of solutions of Hamiltonian equations:
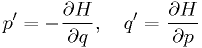
The solutions should conserve 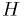 . The Euler and Runge-Kutta schemes don't.
. The Euler and Runge-Kutta schemes don't.
Numerical symplectic ODE solvers
The simplest (and very common) cases arise from 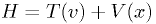 , so that
, so that
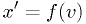 and
and 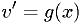 .
.
A 1st-order symplectic version of Euler's equation:
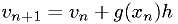
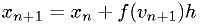
A beautiful 2nd-order symplectic method:
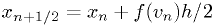
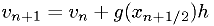
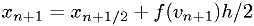
Note these symplectic methods need to distinguish between  and
and 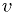 .
.
Assignment
- Implement the 2-nd order symplectic integrator and the 4-th order Runge-Kutta integrator.
- Test them with oscillator and orbit equations.
- You can reuse as much of the code on the course web page as you like.