Class 6: Numeric ODE integrators; API design and testing

The basic n-dimensional ODE equation

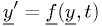
$\underline{y}' = \underline{f}(\underline{y},t)$

where 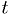is the independent variable, 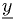$\underline{y}$ are the dependent variable, and underlines denote vectors.

This looks like a first-order ODE, but it can represent a higher order ODE with a simple "chain" of variables. E.g., 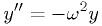$y'' = -\omega^2 y$ can be implemented by defining 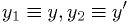$y_1 \equiv y, y_2 \equiv y'$ , and

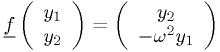
$\underline{f}\left( \begin{array}{c} y_1 \\ y_2 \end{array} \right) = \left( \begin{array}{c} y_2 \\ -\omega^2 y_1 \end{array} \right)$

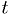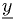We can also eliminate explicit dependence by making it one of the elements of $\underline{y}$ .

Note: I'm going to drop the underlines now, but 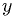and 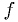are still vectors.

Numerical solutions

We want to find approximate numeric solutions of some accuracy without already knowing the analytic solution.
For initial value problems, we do this by integrating the ODE in discrete steps in 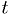. The step size is conventionally called .
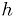The easiest starting point is the Taylor series.

Euler 1st order:

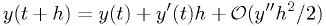
$y(t+h) = y(t)+y'(t) h + {\cal O}(y'' h^2/2)$

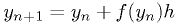
$y_{n+1} = y_n + f(y_n) h$

2nd order

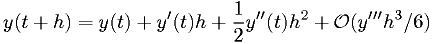
$y(t+h) = y(t)+y'(t) h + \frac{1}{2}y''(t)h^2 + {\cal O}(y''' h^3/6)$

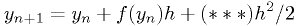
$y_{n+1} = y_n + f(y_n) h + (***) h^2/2$

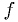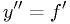*** If we require that only the function be specified in analytic form, not its derivatives, then y''=f' has to be estimated from previous or future values of 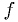in some clever way.

Heun's method: 2nd order

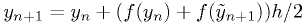
$y_{n+1} = y_n + (f(y_n)+f(\tilde{y}_{n+1})) h/2$

where 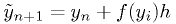$\tilde{y}_{n+1} = y_n + f(y_i) h$ is the Euler's method approximation for $y_{n+1}$ .

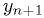This is equivalent to

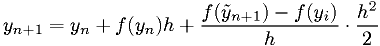
$y_{n+1} = y_n + f(y_n)h + \frac{f(\tilde{y}_{n+1})-f(y_i)}{h} \cdot \frac{h^2}{2}$

Fourth-order Runge-Kutta

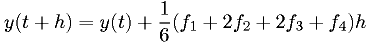
$y(t+h) = y(t) + \frac{1}{6}(f_1 + 2 f_2 + 2 f_3 + f_4) h$

where

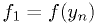
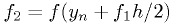
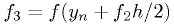
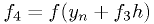
Programming for reusability

General principles:

Don't embed an algorithm everywhere you need it. That forces you to rewrite it repeatedly.
Write once, reuse often!
This is a little more work, but usually pays for itself quickly.
The little bit more work: you have to design an API for your algorithm.

An API for an ODE solver

The API can be very simple: just one function to advance one step.

The ODE step function takes three arguments:

The starting value of 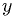. (A vector<double>.)
The function for 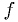. (A pointer to a function.)
The size of the step .

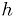There are two options for how to return the updated value:

Actually return the new value.
Update the existing 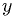"in place" (pass by reference).

The 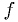function takes a little more thought.

How to define the derivative function?

The straight-forward way: pass-by-value, return a value:

vector <double> f( vector<double> y );

Pass-by-reference (in and out):

void f(const vector<double> &y, vector<double> &f_out);

The second way is up to a factor of 2 faster because it requires less copying of data between memory locations.

API to use in today's assignment

typedef void f_vect_vect_t(const vector<double> &y,
                           vector<double> &f_out);

void rk4step(vector<double> &y,
             f_vect_vect_t * fptr,
             double h);

A note on "name space"

Good "namespace" citizenship:

Choose names unlikely to be used elsewhere. (E.g., "f" would be a bad name for a globally-defined function or type.)
C++ namespaces were designed to help with this.

Testing

Write test cases for your functions.
You need a test independent from your main application!
- Don't be fooled into thinking you can always recognize a wrong answer when you see it. If you already knew the answer to your main problem, you wouldn't be writing this program in the first place.

Test case: oscillators and orbits

We know the solutions to 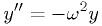$y'' = -\omega^2 y$ and to 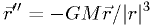$\vec{r} '' = -GM\vec{r}/|r|^3$ . Let's test the Euler ODE solver with that case.

Code: see course web page.

Results of test

Position vs time:

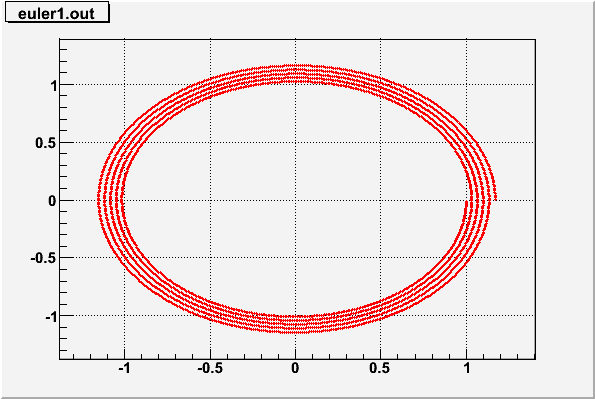
Results of the euler1 test program, showing points spiraling out.

Results of the test program for Euler integration of the simple harmonic oscillator equation. Note how points spiral out.

It's spiralling outward. Energy is not being conserved!

What went wrong?

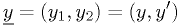Momentarily using the underline notation again, the vector $\underline{y} = (y_1, y_2) = (y,y')$ is a vector in phase space. It is supposed to follow a closed path, but the finite steps in the 1-st order Euler ODE solver don't allow that.

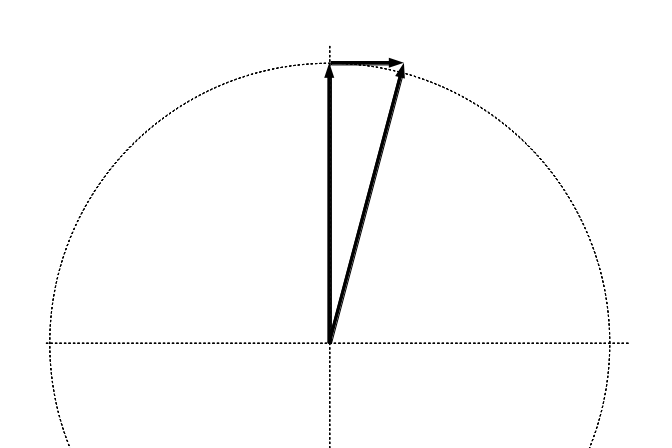
Figure showing addition of finite correction to a vector in perpindicular direction, increasing length of vector.

Addition of a finite correction perpendicular to a vector.

Symplectic ODEs

The harmonic oscillator and orbit problems, and many others in science in engineering, are examples of solutions of Hamiltonian equations:

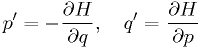
$p' = -\frac{\partial H}{\partial q}, \quad q' = \frac{\partial H}{\partial p}$

The solutions should conserve 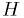. The Euler and Runge-Kutta schemes don't.

Numerical symplectic ODE solvers

The simplest (and very common) cases arise from 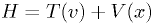H=T(v)+V(x) , so that 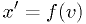x'=f(v) and v'=g(x) .

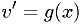A 1st-order symplectic version of Euler's equation:

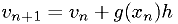
$v_{n+1} = v_n + g(x_n) h$

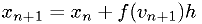
$x_{n+1} = x_n + f(v_{n+1}) h$

A beautiful 2nd-order symplectic method:

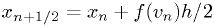
$x_{n+1/2} = x_n + f(v_{n}) h/2$

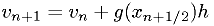
$v_{n+1} = v_n + g(x_{n+1/2}) h$

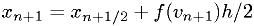
$x_{n+1} = x_{n+1/2} + f(v_{n+1}) h/2$

Note these symplectic methods need to distinguish between 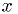and .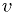

Assignment

Implement the 2-nd order symplectic integrator and the 4-th order Runge-Kutta integrator.
Test them with oscillator and orbit equations.
You can reuse as much of the code on the course web page as you like.