Class 2.5: more on integers and floating point
Integer math
The most important thing to keep in mind here is that division of two integers gives an integer:
1/3 = 0, 2/3 = 0, 3/3 = 1, 4/3 = 1, etc.
In particular:
- (T-32.0)*(5/9) always gives zero (because 5/9 = 0)
- (T-32.0)/(9/5) is the same as T-32.0 (because 9/5 = 1)
Integer ranges
- An unsigned
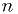 -bit integer can represent values from 0 to
-bit integer can represent values from 0 to
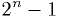 (inclusive).
(inclusive). - A signed
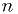 -bit integer can represent values from
-bit integer can represent values from 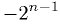 to
to 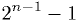 (inclusive). [1]
(inclusive). [1]- The lower
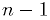 bits are an unsigned
bits are an unsigned 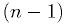 -bit integer, and the
highest bit ("sign bit") means "subtract
-bit integer, and the
highest bit ("sign bit") means "subtract 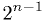 if set".
if set".
- The lower
| [1] | This assumes the CPU uses "twos complement" form for signed integers, which all CPUs I know of today do. |
Example: 8-bit signed integer
| Binary | Decimal |
|---|---|
| 00000000 | 0 |
| 00000001 | 1 |
| 01111111 | 127 |
| 10000000 | -128 |
| 10000001 | -127 |
| 11111111 | -1 |
In many (but not all) computer systems, a signed char happens to be an 8-bit signed integer.
Real numbers: Floating point representation
A positive real number x can be written in base-2 as
x = (1 + M/2m) * 2E-b,
where M and E are unsigned integers, m is the number of bits in M, and b is a constant integer.
Add a sign bit, and let M=E=0 be a special case for zero, and we have ourselves a "floating point" representation of real numbers.
The representation is exact if x doesn't need any bits in M below a certain point. Example: x = 1.875 = 15.0/8.0.
The representation can only be approximate if x doesn't nicely turn into a short binary fraction. Example: x = 0.2 = 1.0/5.0.
Real number math
Math with real numbers (i.e., floating point) works "as you'd expect":
1.0/4.0 = 0.25, 1.0/3.0 = 0.33333333333333331, 1.0/5.0 = 0.20000000000000001
The most important point to keep in mind is if you want to do real number math with a constant that happens to be an integer, just put in a decimal point.
In particular, if you're converting Fahrenheit to Celsius:
- (T-32.0)*(5./9.) does what you want.
- (T-32.0)/(9./5.) also does what you want.
They give very slightly different answers for T=55 because neither 5./9. or 9./5. is exactly an integer divided by a power of two.