Nucleation!!!!!!!!!

Figure 2

Figure 1

Figure 3

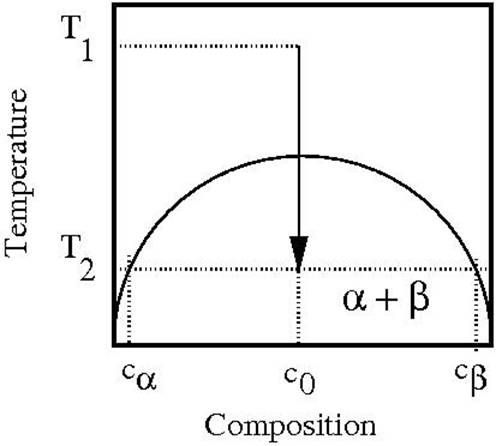
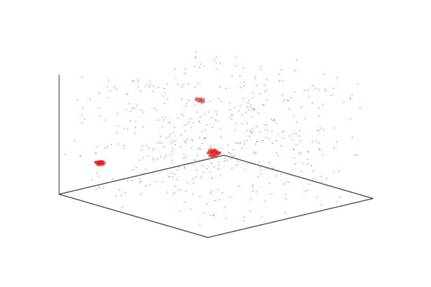
At a given temperature, there is a volume fraction that is ideal for the growth of nucleating clusters in a system. These conditions appear near the boundary of the phase diagram that exists if you plot temperature as a function of concentration for a given system (figure 1). Figure 2 shows the morphology of three nucleating clusters at a concentration k=8, T=.15kt, number of monomers=1000, and box size =128 (volume fraction=.00025). Nucleating clusters grow uniformly and have a compact structure, resembling that of a sphere with a fractal dimension nearing the value of 3. 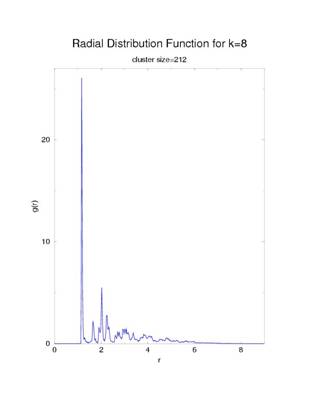To study the structure of the nucleating clusters, I plotted the radial distribution function of the largest cluster in a system as a function of radial distance (figure 3). To see an image of this see the section on Lysozyme. The slightly sharp peaks are indicative of a more tightly bound structure due to the large probability that a monomer will be at a given position. In contrast a liquid would have very broad distribution with dull peaks due to the particles ability to move around more freely.