Potential!!!!!!

Figure 1

Figure 2

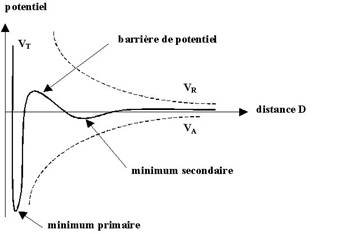
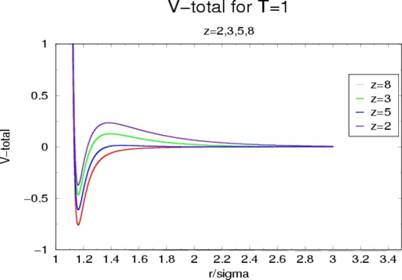
Figures (1) shows a potential as a function of radial distance radius (the separation distance between two monomers divided by the diameter of a particle) plot for an attractive potential (modified Lennard-Jones) and a repulsive potential (Yukawa) respectively along with what happens when they are added together.  Figure (3) shows the total potential of my system at 4 different salt concentrations.  Notice that at the lowest concentration, the attractive and repulsive potentials combine to create a potential barrier that is around 70 percent the size of the potential well.  However, as the salt concentration is increased, the depth of the potential well is increased while the height of the potential barrier has decreased.  This occurs due to the fact that the monomers can come closer together due to the increase in the neutral barrier surround the monomers, allowing the monomers to come closer together and feel the short range Van der Waals attraction more effectively.  The potential barrier at lower salt concentrations is indicative of RLCA, due to its implication of the existence of a finite probability that the particles will not irreversibly stick together (that the particle will not make it to the potential well due to the size of the barrier).  Thus, simulations at these concentrations should yield compact clusters, but it should also have some monomers still left in the system.  However, at the higher concentrations, one can see the barrier does not exist.  This should lead to DLCA under these conditions, and the aggregates formed should be stringy and fractal like due to their tendency to fall into the deep well.