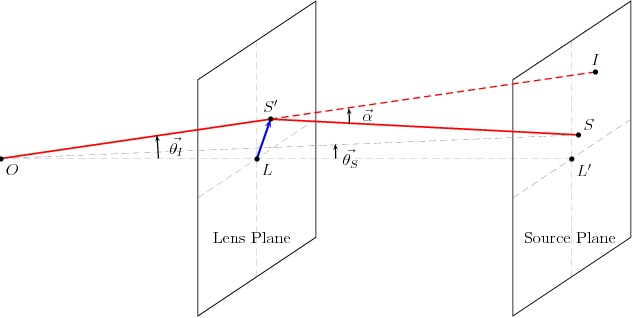
Figure: Gravitational lensing diagram for thin lens approximation: The light leaving the source amath S endamath in the source plane gets deflected by an angle amath \alpha endamath as it approaches the lens plane consisting of the lensing mass amath L endamath at the origin. Then it follows the deflected path amath S'O to get to the observer at O, which is practically us looking at distant stars, galaxies or clusters of galaxies. amath OS' endamath projected back on the source plane gives the image position amath I endamath. Usually, if the the lensing mass is symmetric amath L', S, I endamath lie on the same line as depicted in the figure but in general that is not true for asymmetric lenses.
All the angles are practicall very small. Looking at the vectors in the source plane, it is obvious, amath \vec{L' I} = \vec{L' S} + \vec{S I} endamath which is used to construct the lens equation amath \vec{\theta} = \vec{\theta_S} + \frac{D_{L S}}{D_{O S}} \vec{\alpha} endamath where the distances are not ordinary Eucledean distances but angular diameter distances.