Homework set #10 (due 12/3/02)

  1. Prove that the expressions in eq. (7.28) are identical to those given in eq. (7.27).
  2. problem 7.1.
  3. problem 7.2.

 

  1. Use of a pile of plane-parallel plates to produce polarized light:

Show that the ratio of the transmission  coefficient for perpendicular vs the transmission coefficent for parallel light upon passing the surface once is given by cos2(), where the two angles are the incident and the refraction angles, resepctively.  Show that if such a light passes thru a thin film, then the ratio above becomes cos4().

          If you have five such thin films stack together, and the incident angle is at the  Brewster angle, show that this ratio is about 0.2 if n=1.5.  (n=1 for the air.)

 

  1. In this exercise you calculate the phase change of the reflected wave under the  total internal reflection condition.

Let a plane wave travelling in a medium with index of refraction  is reflected from a medium with index of refraction  where . Show that for incident angle  greater than the critical angle, the phase change for the an incident wave where the electric field is parallel to the plane of incidence is

 

                                     ,

 

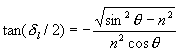and for electric field perpendicular to the plane of incidence the phase change is

 

 

                                       

 

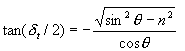
                where n=.   Aslo show that

                       

This shows that one can use total internal reflection to change a plane wave into a circularly polarized wave.

 

 

 

 

Homework set #9 (due 11/21/02)

 

1.    In this exercise you will calculate the pressure due to a plane wave when it is reflected from a planar surface.  Consider the case that the electric field of the plane wave is polarized parallel to the plane of incidence. The incident angle is  .


   (a) the elementary method.
         Calculate the momentum of the incident plane wave. Calculate the change of momentum when the incident wave is reflected. From this calculate the pressure.


   (b) Use the formula involving the Maxwell stress tensor.
         Calculate the electric and magnetic field near the planar surface. Then follow the definition to obtain the pressure which is the diagonal component of the Maxwell stress tensor.

 

2.    Calculate the total force due to the radiation pressure on a plane which is perpendicular to the direction of the sunlight. The plane has an area of  1 km2  and the intensity of the sun at the surface of Earth is 1350 W/m2. Make sure that you use correct numbers (depending on the units used) in the calculation.

 

3.   A Ti.Sapphire laser has a peak intensity of 1020 W/cm2, calculate the peak electric field in units of MV/m. What is the electric field on an electron which is at 1 Bohr radius from the center of the hydrogen atom?  The intensity of the sun at the surface of Earth is 1350 W/m2. What is the total power received on the surface of Earth, and compare the number with the total power received in 1 cm2 of the Ti:Sapphire laser.

 

 

 

Homework set #8 (due 11/14/02)

 1.   A current I flows through a resistor R in the form of a long
    straight wire. Show that the poynting vector flows radially inward through
    the surface of the wire with the correct magnitude to  produce the Joule heating.

 

2.  This problem is adopted from the book of Heald and Marion, 4-12 and 4-13. It
is a good exercise of manipulating the time-dependent Maxwell equations.

   Consider a parallel-plate capacitor consisting of two circular plates. The radius of
the plate is a and the plate separation is h and the medium is filled with a dielectric which
has dielectric constant . The capacitor is charged by connecting to a battery
with EMF  V0 and a series resistor R. If the circuit is closed at t=0 find the following
quantities within the capacitor as a function of time. Neglect the edge effect.
(a) The electric field.
(b)  the magnetic field.
(c) the Poynting vector.
(d) the total field energy.
(f) the scalar potential.
(g) the vector potential

3. Continue problem 3, but now assume that the material between the plates have
conductivity  in addition to being a dielectric.  Forget the resistor in problem
w2. This capacitor is charged to a potential V0 by a battery and then disconnected at
t=0.
(a) Find the free charge on the capacitor as a function of time.
(b)  Find the conduction current, the displacement current density.
(c) Find the magnetic field H within the capacitor,

 

 

Homework set #7 due (11/5/02)

5.3

5.6

5.13

 

Homework set #6 due (10/10/02)

  1. problem 4.2
  2. problem 4.6
  3. problem 4.8

 

Homework set #5 due (10/1/02)

1.      Problem  3.17

2.      Problem 3.22

 

 

 

Homework set #4 due (9/24/02)

  1. Problem 3.2. Part (a)

Hint: treat the problem as a uniformly charged sphere plus a negative charge on the northern cap. Then consider the potential due to the northern cap using the results worked out from the class. See example in Fig. 3.4.  You need to use eq. (3.28).

  1. Problem 3.7.
  2. problem 3.9—this is a simple exercise for you to set up the series solution in cyclindrical coordinates. Write down the general expression with the boundary conditions incorporated.

 

 

 

 

 

Homework set #3 (due 9/17/02)

  1. problem 2.2
  2. problem 2.7

      3.   problem  2.13

 

 

Homework set #2  (due 9/10/02)

 

  1. Problem 1.9. (consider only parallel plates case)
  2. Problem 1.10

 

  The next three are just simple exercises.

  1. Derive eq. (2.5) of Jackson.
  2. Eq. (2.6) of Jackson shows that the force between charge q and the induced charges on the conducting sphere varies inversely with the cubic power of y. If the distance y of the charge q is now measured from the surface of the sphere, how is the force depends on y? Justify your result.
  3. Eq. (2.15) gives the induced surface charge, calculate the dipole moment from this surface charge and show that it is identical to the dipole moment due to the two image charges.

 

Homework set 1:

Jackson pp50-52  (due 9/03/02)

    1.1;   1.3;  1.4;  1.5;    1.6a,b;